13: 道路ネットワーク
はじめに
今回の演習では、道路ネットワークを使った地域分析をRで実行する方法ついて学びます。
道路距離と直線距離
これまでの演習では、学校や保育所など施設までの距離や、地域間の距離を測る時にsf::st_distance関数を使って、2地点間の距離を直線距離で計測し、分析に利用していました。
しかし私たちは、通学にしても通勤にしても道路上を移動します。 なので、本来であれば道路距離を使って分析した方が、より正確な数値を使うことができるという意味では、望ましいです。
にもかかわらず、道路距離でなく直線距離を利用した理由はいくつかあります。 理由の第一は、直線距離を利用すると問題を幾何学的に定式化できるので、状況を説明しやすかったり概念が理解しやすかったりする、ということです。 また2つ目の理由としては、かつては、道路網データを整備したり、ネットワークデータをコンピュータで大量かつ高速に処理することのコストが高かった、ということも挙げられると思います。
ところで、道路距離と直線距離はどのような関係にあって、どのくらい異なっているのでしょうか?
腰塚・小林(1983)は、実際の道路網データを使って、都市内(新宿区・江東区・目黒区)および都市間(茨城県)の道路距離(\(R\))と直線距離(\(D\))を計測し、最小二乗法からおおよそ都市内でおよそ\(R=1.3D\)、都市間でおよそ\(R=1.21D\)であるとの結果を得ました(道路距離は直線距離の1.3倍というこの論文の成果が、道路距離を直線距離で代替する際の目安の1つになっています)。
森田・鈴木・奥貫(2014)は、全国112都市を対象として、都市内の道路距離と直線距離の関係を分析し、その結果、道路距離と直線距離の比(道直比)の112都市の平均は1.3035となり、腰塚・小林(1983)の結果とほぼ等しい結果を得たとしています。 しかし、112都市を詳しく見ると、道直比が最小の一宮市(1.1260)から最大の静岡市(1.9235)まで都市によって道直比がかなり異なることを指摘していて(ちなみに佐賀市の道直比は1.3833)、 既知の道直比を安易に使わないで、分析対象地域の道路網をあらかじめ検討しておく必要があると述べています。
近年では、OpenStreetMapなど利用可能な、道路ネットワークが登場し、道路網データ取得のコストが大幅に低下しました。
グラフ理論の基礎用語
ネットワーク(グラフ)は、エッジとノードで構成されます。
- ノードは頂点あるいは節点とも呼ばれます。
- エッジは辺とも呼ばれ、ノード間の結びつきを表します。
- エッジはウェイト(重み)を持つ場合があります。ウェイトは、ノード間の結びつきの強弱を表します。
- あるノードに接続するエッジの本数を次数(ディグリー)といいます。
- 2つのノード間を複数のエッジが結んでいる場合、その辺を多重辺(多重エッジ)といいます。
- あるノードから同じノードへ戻るエッジをループといいます。
- 多重辺やループを含まないグラフを単純グラフといいます。
- ノードから別のノードまで1つ以上のエッジでつないだ道を経路(パス)といいます。
- どの2つのノードも経路で結ばれているグラフを連結グラフといいます。
- 連結でないグラフを非連結グラフといいます。
- 非連結グラフを構成する連結グラフを成分(コンポーネント)といいます。
演習
準備
パッケージのロード
library(tidyverse)
library(sf)
library(jpstat)
library(jpgrid)
library(osmdata)
library(tidygraph)
library(sfnetworks)
library(ggrepel)空間データのダウンロード
今回の演習では、医療機関のポイントデータと、メッシュ人口のデータを利用します。
医療機関データ
国土数値情報から、佐賀県の医療機関データ(令和2年)をダウンロードしてください。
ダウンロードしたP04-20_41_GML.zipをダウンロードフォルダで展開し、 できたフォルダ(P04-20_41_GML)を、今回のプロジェクトのdataフォルダに移動してください。
メッシュ人口データ
地域メッシュ統計から、佐賀市中心部の250 mメッシュごとの65歳以上人口を取得しましょう。
以下の例では、先週に引き続き、jpstatパッケージを利用しています。
Sys.setenv(ESTAT_API_KEY = keyring::key_get('e-stat'))
mesh <- estat(statsDataId = '8003007580')
mesh# ☐ cat01: 年齢別人口、世帯の種類別世帯数等 [50] <code, name, level, unit, parentCode>
# ☐ cat02: 秘匿地域・合算地域有り [3] <code, name, level>
# ☐ area: M4930 [32,215] <code, name, level>
#
# Please `activate()`.meshdata <- mesh |>
jpstat::activate(cat01) |>
filter(code == '0160') |>
select() |>
jpstat::activate(cat02) |>
select() |>
jpstat::activate(area) |>
select(code) |>
collect(n = 'population') |>
mutate(population = parse_number(population))The total number of data is 32215.データの内容を確認しておきます。
glimpse(meshdata)Rows: 32,215
Columns: 2
$ area_code <chr> "4930010024", "4930010042", "4930010044", "4930010113", "49…
$ population <dbl> 57, 77, 18, 34, 69, 18, 46, 32, 17, 43, 13, 12, 20, 13, 13,…e-Stat APIから地域メッシュ統計を利用するには、統計表のstatsDataIdが必要です。 現時点では地域メッシュ統計のstatsDataIdを知るには、e-Stat APIを使って検索するしかありません。 以下の例は、estatapiパッケージを使ってstatsDataIdを調べる方法の例です。
library(estatapi)
estat_getStatsList(
appId = keyring::key_get('e-stat'),
searchWord = '国勢調査 AND 世界測地系 AND 250Mメッシュ',
surveyYears = '2020',
searchKind = 2
) |> View()メッシュポリゴンはjpgridパッケージを使って作成しましょう。 対象地域を、佐賀駅を含むメッシュを中心としたおよそ10 km四方(縦横それぞれ41メッシュ)の範囲とします。
saga_sta <-
coords_to_grid(130.2973968, 33.26498367917074, '250m')
grid <- saga_sta |>
grid_neighborhood(n = 0:20, type = 'moore') |> first() |>
grid_as_sf(crs = 6668) |> st_transform(6670) |>
mutate(area_code = as.character(grid))mapview::mapview関数で、メッシュポリゴンの位置を確認しておきます。
mapview::mapview(grid, map.types = 'OpenStreetMap')dplyr::left_join関数を使って、メッシュポリゴンに統計データを結合します。 高齢者人口でメッシュ統計地図を作ってみましょう。
grid <- grid |>
left_join(meshdata, by = join_by(area_code))
ggplot() +
geom_sf(aes(fill = population), data = grid) +
scale_fill_distiller(direction = 1) +
theme_minimal()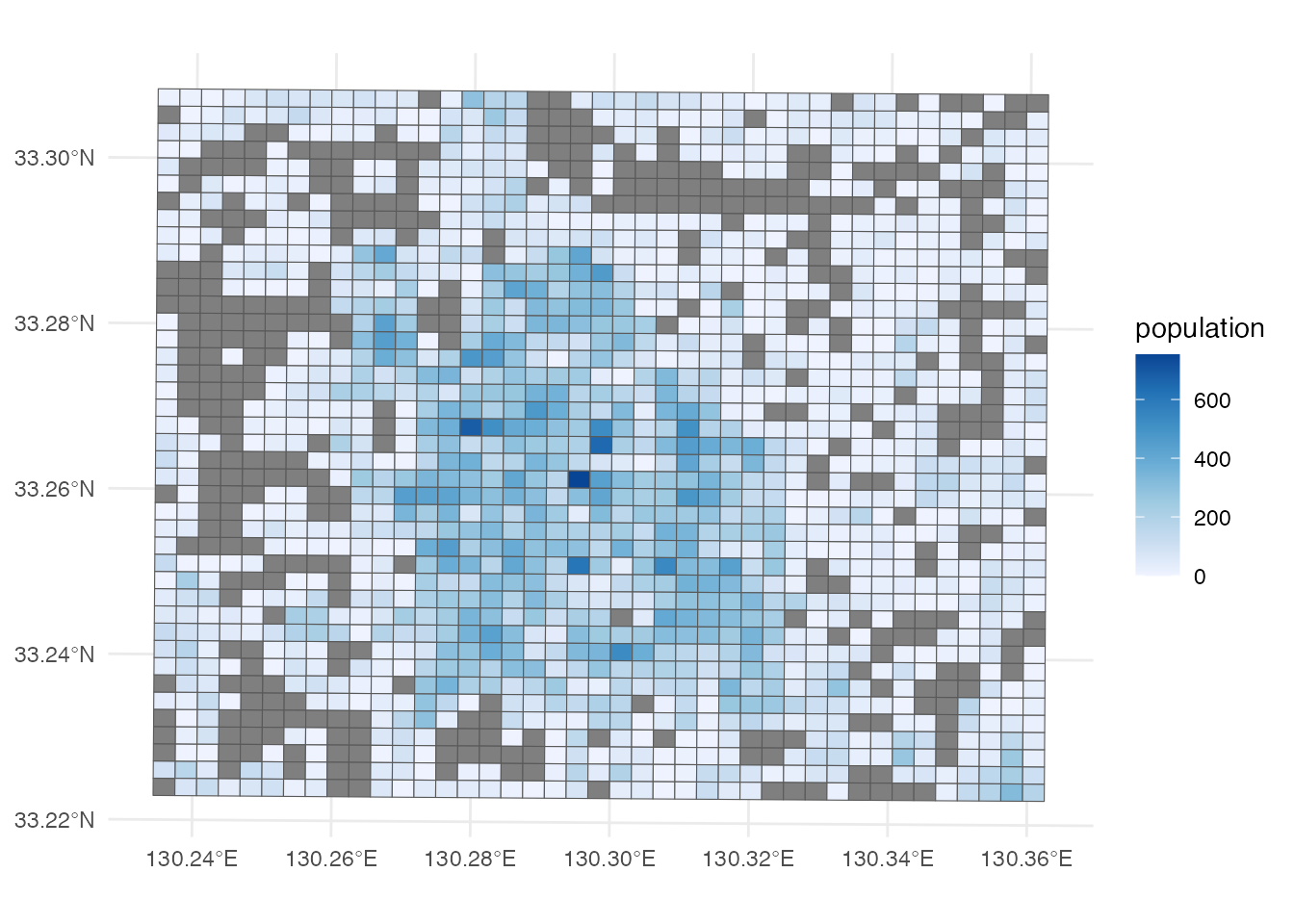
道路網データ
osmdataパッケージを使って、佐賀市中心部の道路網データを取得します。 このパッケージには、OpenStreetMapのOverpass APIをRから利用する関数が用意されています。
まず、osmdata::opq関数を使って、Overpass APIに送るクエリ(要求)を作成しますが、第1引数bboxにデータを取得する地理的範囲を指定します。
bbox <- grid |> st_transform(6668) |> st_bbox()これは、データを取得する地理的範囲の、緯度と経度の上限および下限を意味しています。
bbox_sf <- bbox |>
st_bbox(crs = st_crs(6668)) |>
st_as_sfc() |> st_as_sf() |>
st_transform(6670)sfオブジェクトに変形して、mapview::mapviewを使って地図に表示してみます。
mapview::mapview(bbox_sf, map.types = "OpenStreetMap")それでは、osmdata::opq関数を使って、クエリを作成します。 さらに、osmdata::add_osm_feature関数を使って、取得するフィーチャー(地物)の情報をクエリに追加します。
ここでは、道路(Highway)のフィーチャーを取得するように設定しています。 また、取得する道路の種類は、道路の種別を参考にして決めました。
query <- opq(bbox) |>
add_osm_feature(key = 'highway',
value = c("trunk", # 国道
"trunk_link", # 国道間又は国道への連絡路や加速車線
"primary", # 主要地方道
"primary_link", # 主要地方道への連絡路や加速車線
"secondary", # 一般地方道
"secondary_link", # 一般地方道への連絡路
"tertiary", # 一般道(2車線以上)
"tertiary_link", # 一般道路への連絡路
"unclassified", # 一般道(2車線未満)
"residential", # 居住区域内道路
"living_street", # 歩行者優先道路
"service", # 敷地内道路
"track")) # 農道または林道作成したクエリを使って、APIからデータを取得します。 ここでは、osmdata::osmdata_xml関数を使って、XML形式で、dataフォルダに保存しています。 ファイル名は「road.osm」としています。8MBほどのデータがダウンロードされると思います。
osmdata_xml(query, 'data/road.osm')もし、道路網データの取得がうまくいかなった場合には、以下のリンクからデータをダウンロードして、dataフォルダに移動してください。
ダウンロードした道路網データを、sf::st_read関数を使って読み込みます。
road <- st_read('data/road.osm', layer = 'lines')Reading layer `lines' from data source
`/Users/kzktmr/Documents/LectureNotes/data/road.osm' using driver `OSM'
Simple feature collection with 18895 features and 10 fields
Geometry type: LINESTRING
Dimension: XY
Bounding box: xmin: 130.2287 ymin: 33.2111 xmax: 130.3697 ymax: 33.3476
Geodetic CRS: WGS 84network <- road |>
as_sfnetwork(directed = FALSE) |>
st_transform(6670) |>
st_filter(bbox_sf)sfnetworks::as_sfnetworkで、sfオブジェクトをsfnetworkに変換します。 sfnetworkに変換することで、ネットワーク分析のためのtidygraphパッケージと、sfパッケージとを繋ぐことができます。 directed引数は、エッジの向きを考慮するかどうかを意味しています。 ここではFALSEにしていますので、一方通行の規制は無視しています。
sfnetworkには、ノードとエッジのデータは入っていますが、 tidygraph::activate関数を使って、その後の操作でノードとエッジのどちらを参照するかを決定します。
sfnetworkは、st::st_as_sf関数によって、sfオブジェクトに戻すことができます。
network <- network |> activate('edges')
ggplot() +
geom_sf(data = st_as_sf(network), linewidth = 0.2) +
theme_minimal()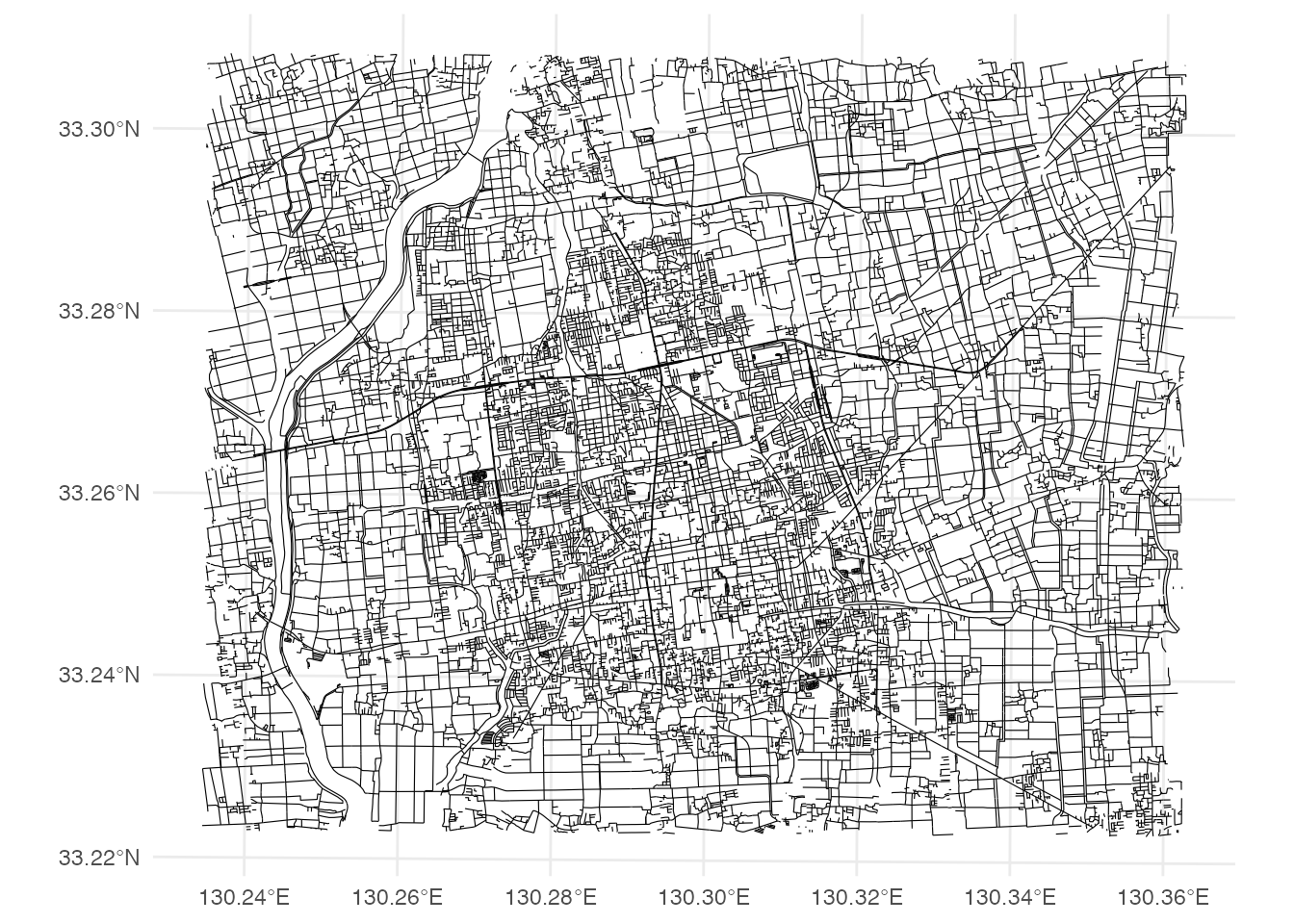
network <- network |> activate('nodes')
ggplot() +
geom_sf(data = st_as_sf(network), size = 0.1) +
theme_minimal()
ネットワークのクリーニング
ネットワーク分析を行う前に、ネットワークのクリーニングを行います。
まず、tidygraph::convert関数とsfnetworks::to_spatial_simple関数を使って、 ネットワークを単純グラフにします。 単純グラフとは、多重エッジやループを持たないネットワークです。 単純でないネットワークでも、問題はないのですが、最短経路探索などの計算を効率的にするために、単純グラフにしておきます。
エッジどうしが交わっているにもかかわらず、その交点にノードがない場合、共有するノードがないので、接続していないことになります。 これが望ましくない場合には、sfnetworks::to_spatial_subdivision関数を使って、 エッジをその交点で分割します。 また、接続しているべきノードが近接しているにもかかわらず接続していない場合にも、 この関数を適用することで接続されることが期待できます。
sfnetworks::to_spatial_smooth関数は、次数が2のノードを取り除きます。
network <- network |>
convert(to_spatial_simple) |>
convert(to_spatial_subdivision) |>
convert(to_spatial_smooth, require_equal = "highway")Warning: to_spatial_subdivision assumes attributes are constant over geometriesまた、OpenStreetMapから作成した道路ネットワークは、必ずしも全てが繋がった(連結の)ネットワークではありません。 今回のネットワークでは、264の成分(コンポーネント)に分かれています。
with_graph(network, graph_component_count())[1] 264ここでは、最大の成分だけを利用することにしましょう。
network <- network |> activate("nodes") |>
filter(group_components() == 1) 最短経路探索
最短経路探索をしてみましょう。 エッジにウェイトを与える必要があります。 sfnetworks::edge_length関数を使って、エッジの長さをweight列としてデータに追加します。
network <- network |> activate("edges") |>
mutate(weight = edge_length())最短経路探索は、sfnetworks::st_network_paths関数を使えば、簡単に求められます。 ここでは、100番目のノードから、500番目と1,000番目のノードまでの最短経路を求めています。
paths <- network |>
st_network_paths(from = 100, to = c(500, 1000),
weights = "weight")最短経路を表示するための関数を定義しておきます。
extract_path <- function(edge_path) {
network |>
activate("edges") |>
slice(edge_path) |>
st_as_sf()
}この関数を使って、最短経路を地図に表示してみましょう。
edges <- paths |> pull(edge_paths) |>
map(extract_path) |> bind_rows()
nodes <- network |> activate("nodes") |>
st_as_sf() |> slice(c(100, 500, 1000))
ggplot() +
geom_sf(data = st_as_sf(network), linewidth = 0.2, color = gray(0.7)) +
geom_sf(data = edges) +
geom_sf(data = nodes) +
theme_minimal()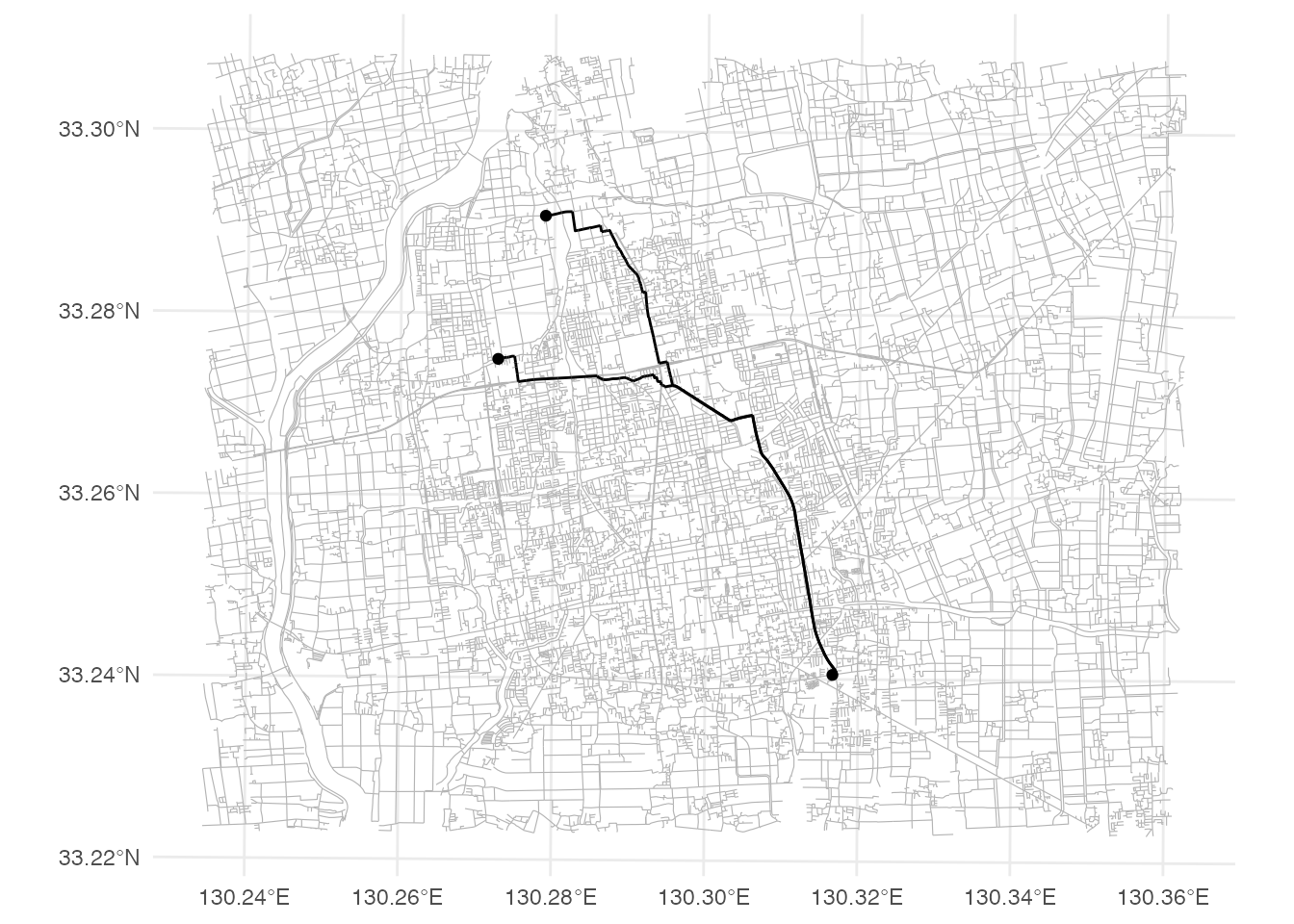
病院データ
sf::st_read関数で病院データを読み込みます。 dplyr::filter関数を使って、歯科診療所を取り除き、救急告示病院だけを抽出します。 さらにsf::st_filter関数で、今回の分析対象範囲に含まれる医療機関だけを取り出しています。
hospital <- st_read("data/P04-20_41_GML/P04-20_41.geojson") |>
filter(P04_001 != "3", P04_009 == 1) |>
select(name = P04_002, beds = P04_008, geometry) |>
st_transform(6670) |> st_filter(bbox_sf) |>
mutate(name = str_remove(name, "^.+[法人|機構]"),
name = str_remove_all(name, "[:space:]"))Reading layer `P04-20_41' from data source
`/Users/kzktmr/Documents/LectureNotes/data/P04-20_41_GML/P04-20_41.geojson'
using driver `GeoJSON'
Simple feature collection with 1129 features and 10 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 129.7644 ymin: 32.97398 xmax: 130.5359 ymax: 33.5971
Geodetic CRS: JGD2011glimpse(hospital)Rows: 17
Columns: 3
$ name <chr> "福田脳神経外科病院", "佐賀中部病院", "春陽会上村病院", "佐賀…
$ beds <int> 40, 160, 198, 292, 604, 19, 88, 75, 19, 120, 60, 19, 177, 90,…
$ geometry <POINT [m]> POINT (-66315.98 27359.65), POINT (-63493.28 29565.07),…病院データをプロットしてみましょう。
ggplot() +
geom_sf(data = st_as_sf(network), linewidth = 0.2, color = gray(0.7)) +
geom_sf(data = hospital, color = 'red') +
theme_minimal()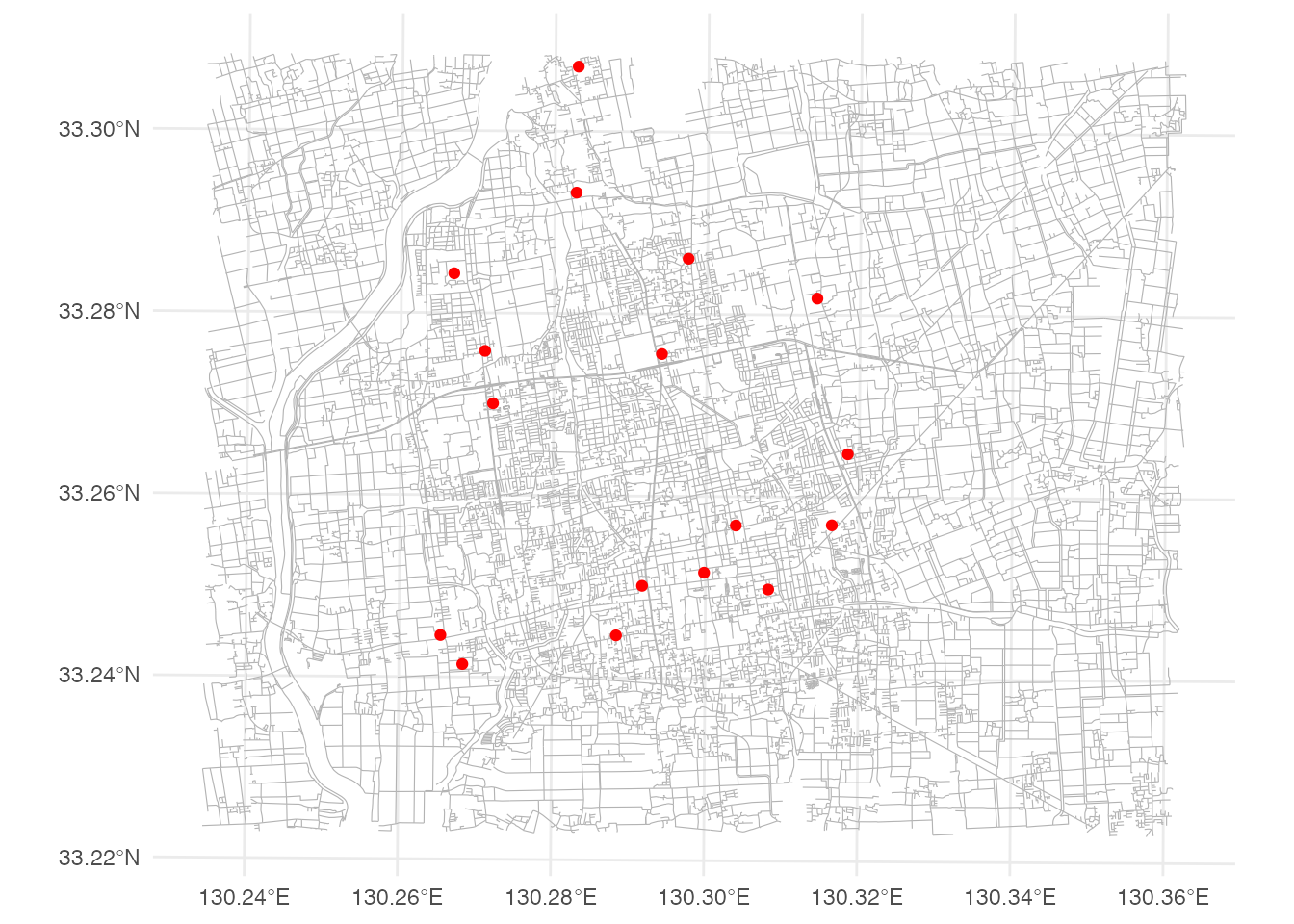
病院データを道路網データにブレンドします。 これは、道路網の中で、各病院に最も近い地点を探し出し、 必要に応じてその場所に新たにノードを挿入する操作です。
network <- network |> st_network_blend(hospital) Warning: st_network_blend assumes attributes are constant over geometriesnetwork <- network |> activate("nodes")
nearest_nodes <- st_nearest_feature(hospital, network)
hospital_nodes <- hospital |>
st_set_geometry(st_geometry(network)[nearest_nodes])病院と、ネットワークの中で最も各病院に近いノードを地図に表示します。
network <- network |> activate("edges")
ggplot() +
geom_sf(data = st_as_sf(network), linewidth = 0.2, color = gray(0.7)) +
geom_sf(data = hospital, color = 'red') +
geom_sf(data = hospital_nodes, color = 'green') +
theme_minimal()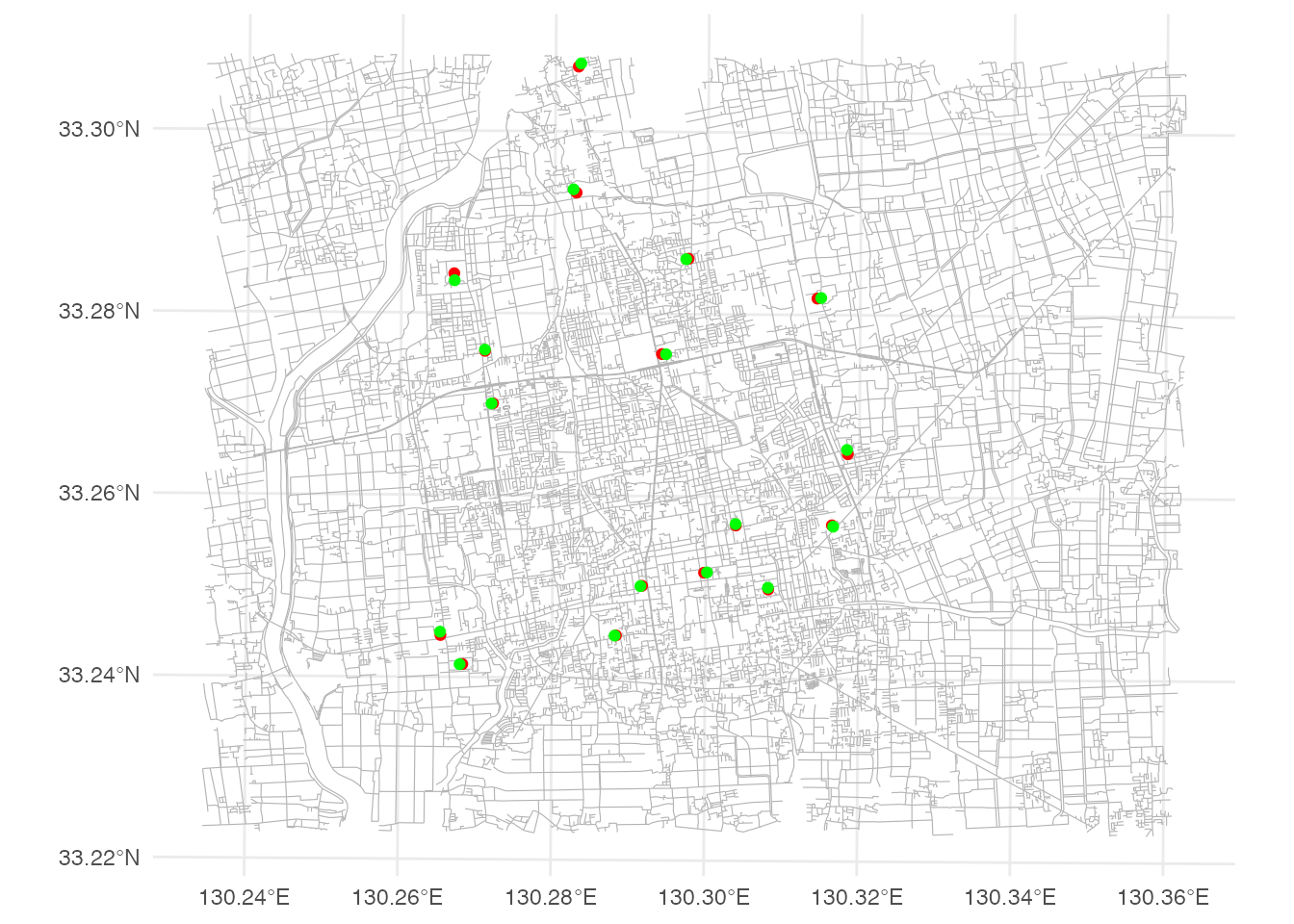
佐賀大学病院から他の全ての病院までの最短経路を探索してみます。
paths <-
st_network_paths(network, from = nearest_nodes[5],
to = nearest_nodes[-5], weights = "weight")最短経路を地図に表示してみます。
path <- paths |> pull(edge_paths) |>
map(extract_path) |> bind_rows()
ggplot() +
geom_sf(data = st_as_sf(network), linewidth = 0.2, color = gray(0.7)) +
geom_sf(data = path, color = 'red') +
geom_sf(data = hospital, color = 'red') +
theme_minimal()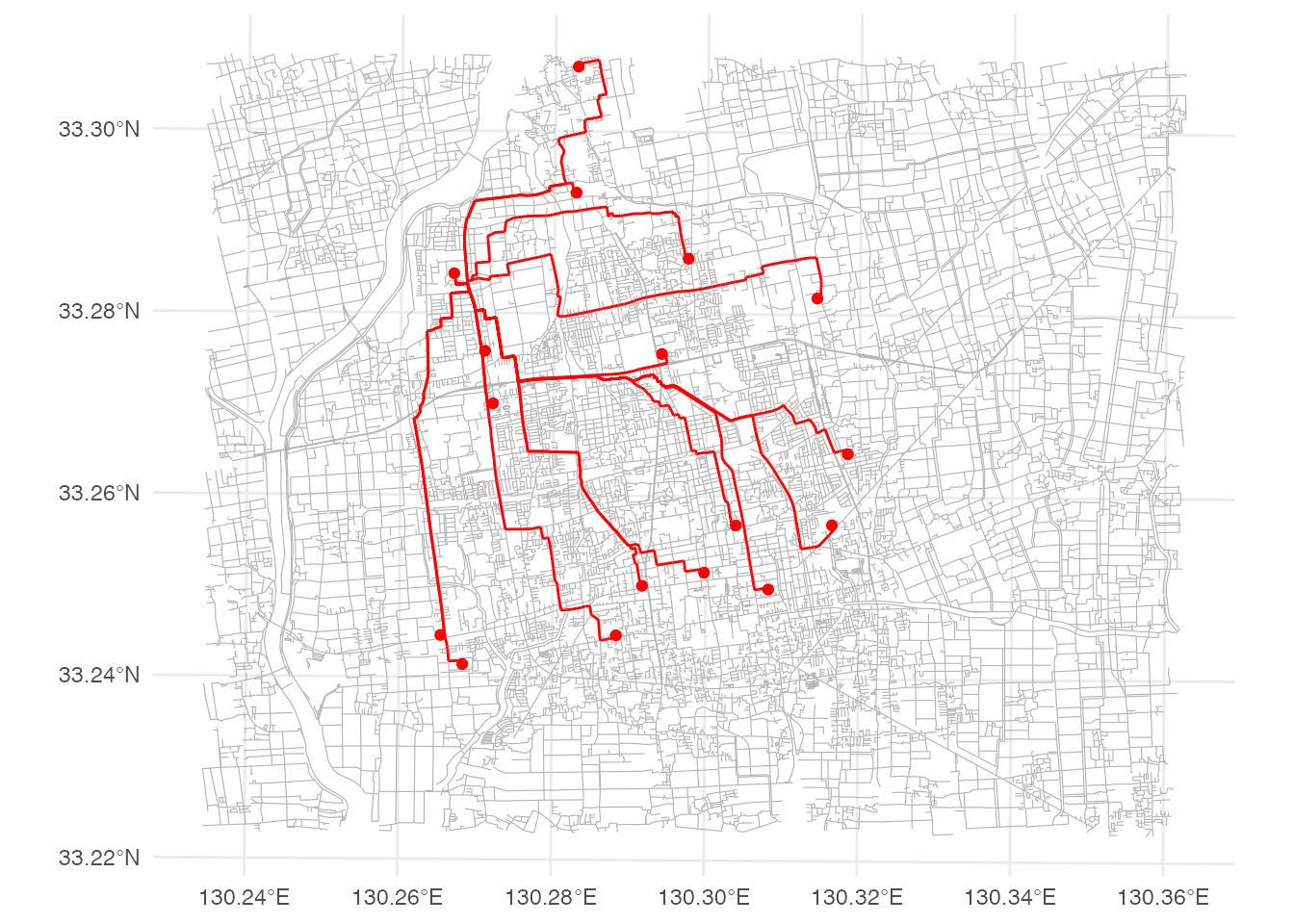
高齢者の分布と病院の立地
高齢者の分布と病院の立地について分析してみましょう。
人口データがNAのメッシュを削除し、 メッシュの代表点をsf::st_centroid関数で作成します。
grid <- grid |> filter(!is.na(population))
grid_p <- grid |> st_centroid()Warning: st_centroid assumes attributes are constant over geometries先ほどの病院データと同様に、メッシュ代表点をネットワークにブレンドします。 これで、メッシュと病院との間の道路距離を測れるようになりました。
network <- network |> st_network_blend(grid_p) |>
activate("edges") |>
mutate(weight = edge_length())Warning: st_network_blend assumes attributes are constant over geometriessfnetworks::st_network_cost関数は、ネットワークの距離行列を計算します。 ここでは、各メッシュから全ての病院への距離計算し、それを1291×17の行列として返しています。
dist_mat <-
st_network_cost(network,
from = grid_p, to = hospital,
weights = 'weight')
dim(dist_mat)[1] 1291 17各メッシュから、道路距離で最も近い(最短距離の)病院を調べます。 つまり、距離行列において、行ごとに何番目の数字が最小かを調べればよいです。 ここでは、
nearest_hospital <- apply(dist_mat, 1, which.min)
grid <- grid |>
mutate(hospital = factor(nearest_hospital))最寄りの病院によってメッシュを塗り分けてみましょう。
ggplot() +
geom_sf(aes(fill = hospital), data = grid) +
geom_sf(data = hospital) +
scale_fill_discrete(guide = 'none') +
theme_minimal()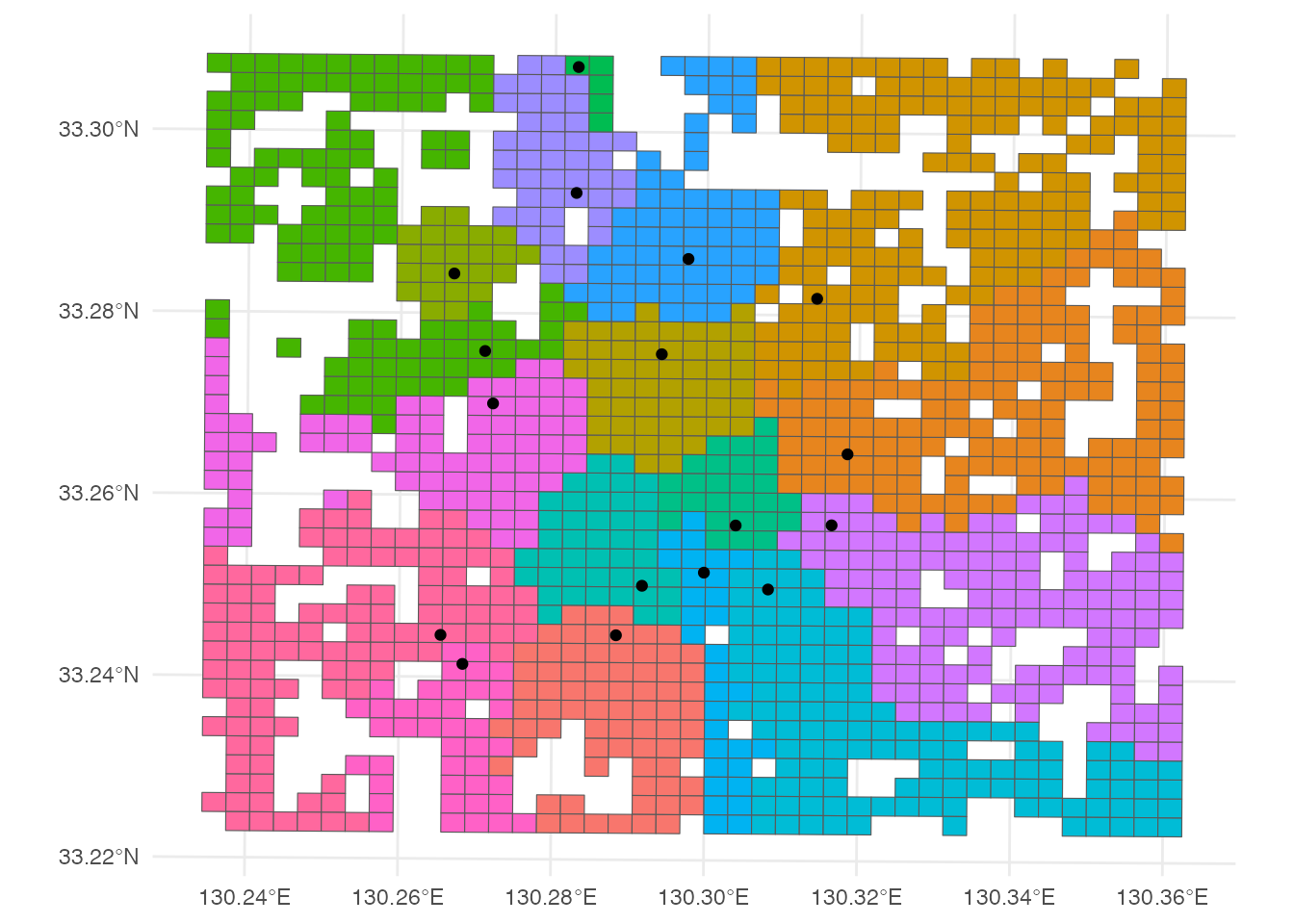
なんだか、ちょっとボロノイ図に似ていますよね? 最も近い施設がどこか、という基準で領域を分割するという概念は、ボロノイ図と共通です。 ということで、少し話が脱線しますが、病院を母点とするボロノイ図を描いて、地図に重ねてみましょう。
bbox_sf <- bbox_sf |> st_transform(6670)
voronoi <- hospital |>
st_union() |> st_voronoi() |>
st_collection_extract(type = "POLYGON") |>
st_intersection(bbox_sf) |> st_sf()
ggplot() +
geom_sf(aes(fill = hospital), data = grid) +
geom_sf(data = voronoi, fill = NA, linewidth = 1, ) +
geom_sf(data = hospital) +
scale_fill_discrete(guide = 'none') +
theme_minimal()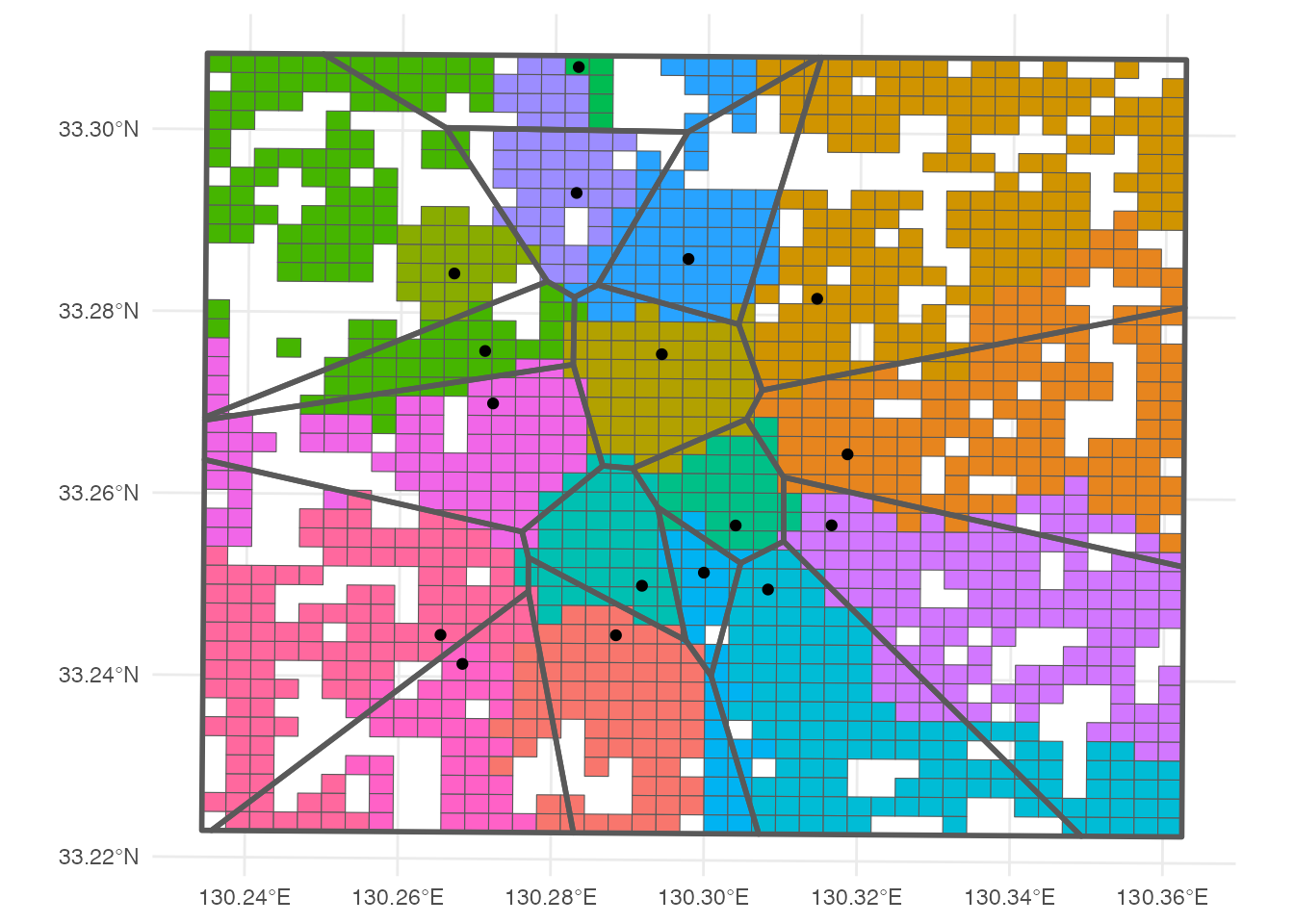
さて、話を戻しましょう。 最寄りの病院に、メッシュの全ての高齢者を割り当てた場合、その病院ごとの人数はどのくらいになるでしょうか。 これは、全員が最寄りの病院を利用するという(強い)仮定のもとで、各病院の需要を考えていることに相当します。
これを計算するには、gridデータを最寄りの病院でグループ分けして、グループごとに人口を合計すればいいですね。
population <- grid |> st_drop_geometry() |>
group_by(hospital) |> summarise(population = sum(population)) |>
ungroup() |> select(population)
hospital <- bind_cols(hospital, population)
ggplot(hospital, aes(x = beds, y = population)) + geom_point() +
geom_text_repel(aes(label = name)) +
theme_minimal()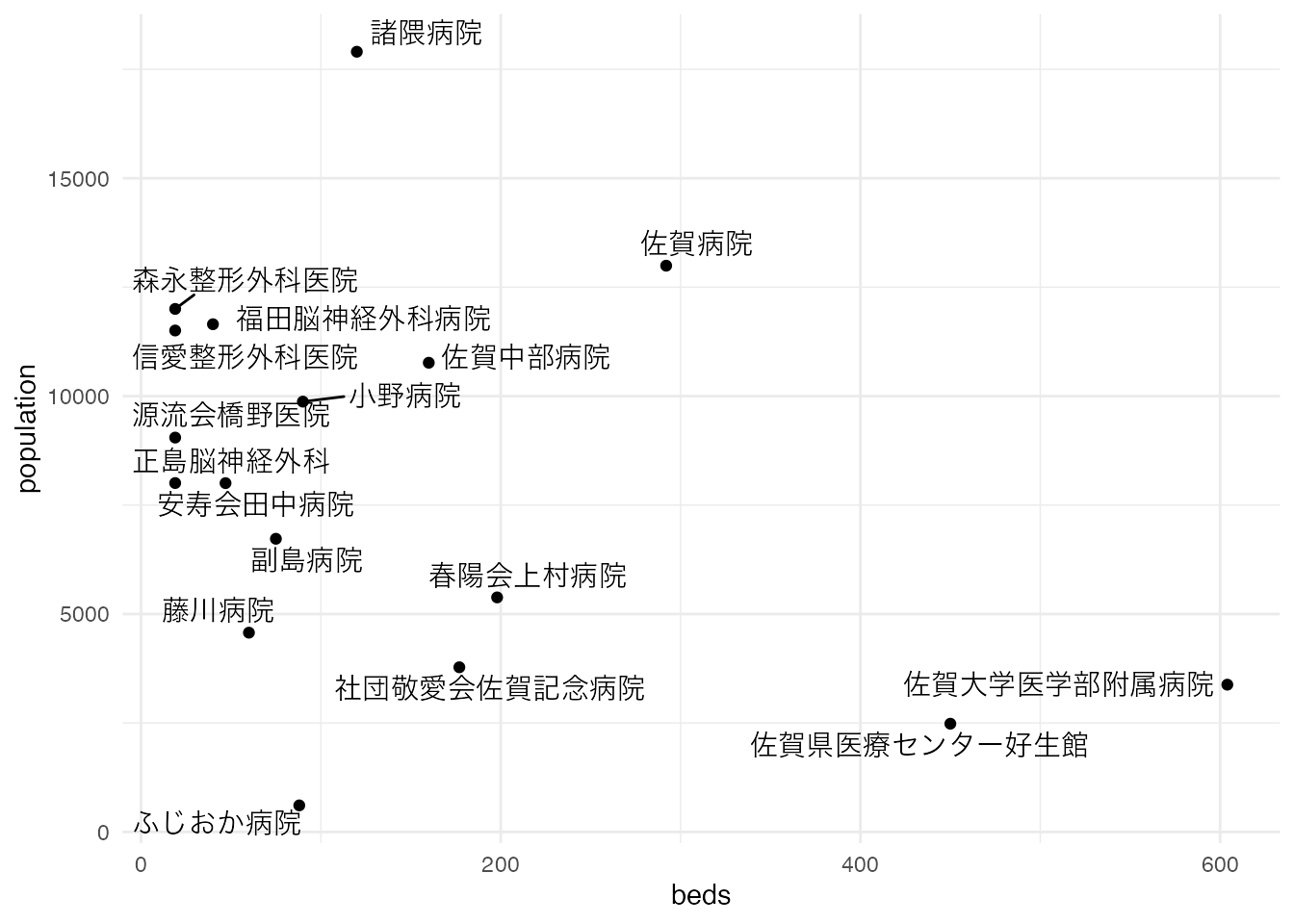
ここでは、各病院の想定需要と病床数のグラフを描いたのですが、あまりいいグラフとは言えませんね。 佐賀大学病院と佐賀県医療センターは、佐賀県に2つしかない災害拠点病院ということもあり、病床数がとても多くなっています。 また病床数が少ない病院は、病院名に「外科」「整形外科」「神経外科」がつく病院が多いです。
次に、病院側から見た(供給側の)視点に立って、 病院から道路距離で5kmの範囲に居住している高齢者数を集計してみます。
within5kmは、距離行列の数字が5km以下(TRUE/FALSE)の論理型のマトリックスです。 病院から5 km以内の人口を、人口(ベクトル)と行列との行列積によって計算しています。
within5km <- dist_mat <= units::set_units(5000, m)
hospital <- hospital |>
mutate(population5 = as.vector(grid$population %*% within5km))
ggplot(hospital, aes(x = beds, y = population5)) + geom_point() +
geom_text_repel(aes(label = name)) +
theme_minimal()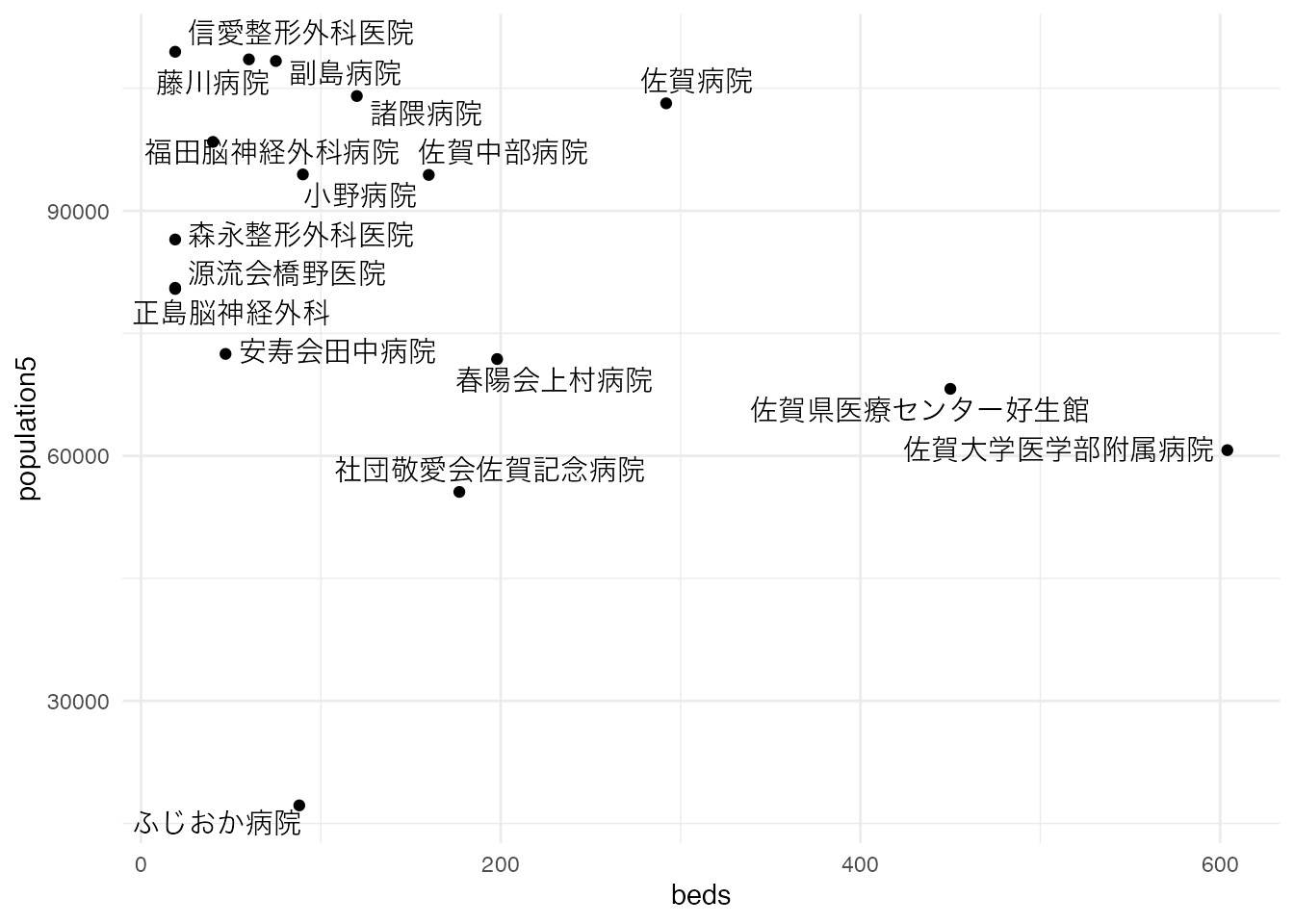
最後に、患者側から見た(需要側の)視点に立って、 各メッシュから道路距離5km以内でアクセス可能な病院数を数えてみましょう。 rowSums関数は、行列の行和を求める関数です。
結果をメッシュポリゴンの塗り分け地図にしてみましょう。 色が濃いメッシュほど周辺に病院が多い地域だということを意味しています。 佐賀市中心部においては、佐賀駅よりもやや西側に病院が立地しているため、それを反映した図になっています。
grid <- grid |>
mutate(hospital5 = rowSums(within5km))
ggplot() +
geom_sf(aes(fill = hospital5), data = grid) +
scale_fill_distiller(direction = 1) +
theme_minimal()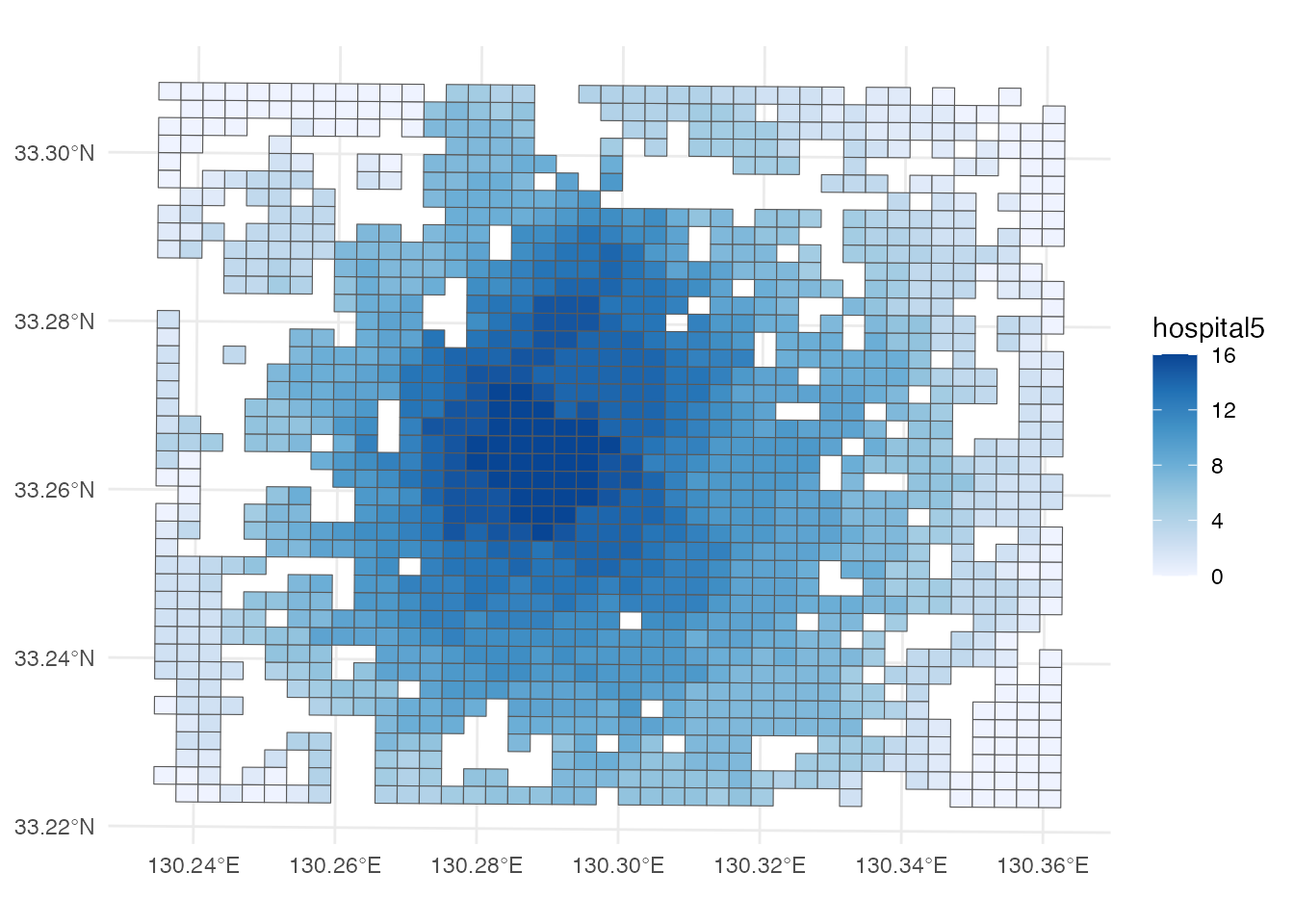
まとめ
今日は、道路距離と直線距離の関係についての研究を紹介した上で、実際にRで道路距離を計測する方法を紹介しました。
OpenStreetMapは、誰でも自由に地図を使えるように、みんなでオープンデータの地理情報を作るプロジェクトです。 地図の精度には問題がないとは言えないかもしれませんが、このプロジェクトのおかげで、道路網データを無料で入手することができます。
道路距離と直線距離による分析結果を見比べると、やはり両者には差がありました。 道路距離を使った分析と直線距離を使った分析のそれぞれに、メリットとデメリットがありますので、状況に応じて、両者を使い分けられるようにしておくと良いと思います。
