8: 立地分析

更新日

2025年6月11日

はじめに

今回から3回にわたって、これまでの講義内容の復習を兼ねたRを使った立地分析の演習を行います。今日の演習では、いろいろな空間データをつかって、佐賀県の待機児童について考えてみることにします。

待機児童とは、保育園等の利用を申し込んだ児童数から、実際に保育園等を利用している児童の数を除いた人数のことをいいます。つまり、保育園等を利用したいのに利用できずにいて、保育園等に空きが出るのを待っている（待機している）人数のことです。

日本の待機児童は、2017年の26,081人をピークに減少を続けており、2024年の待機児童は、ピークのおよそ10分の1となる2,567人でした。

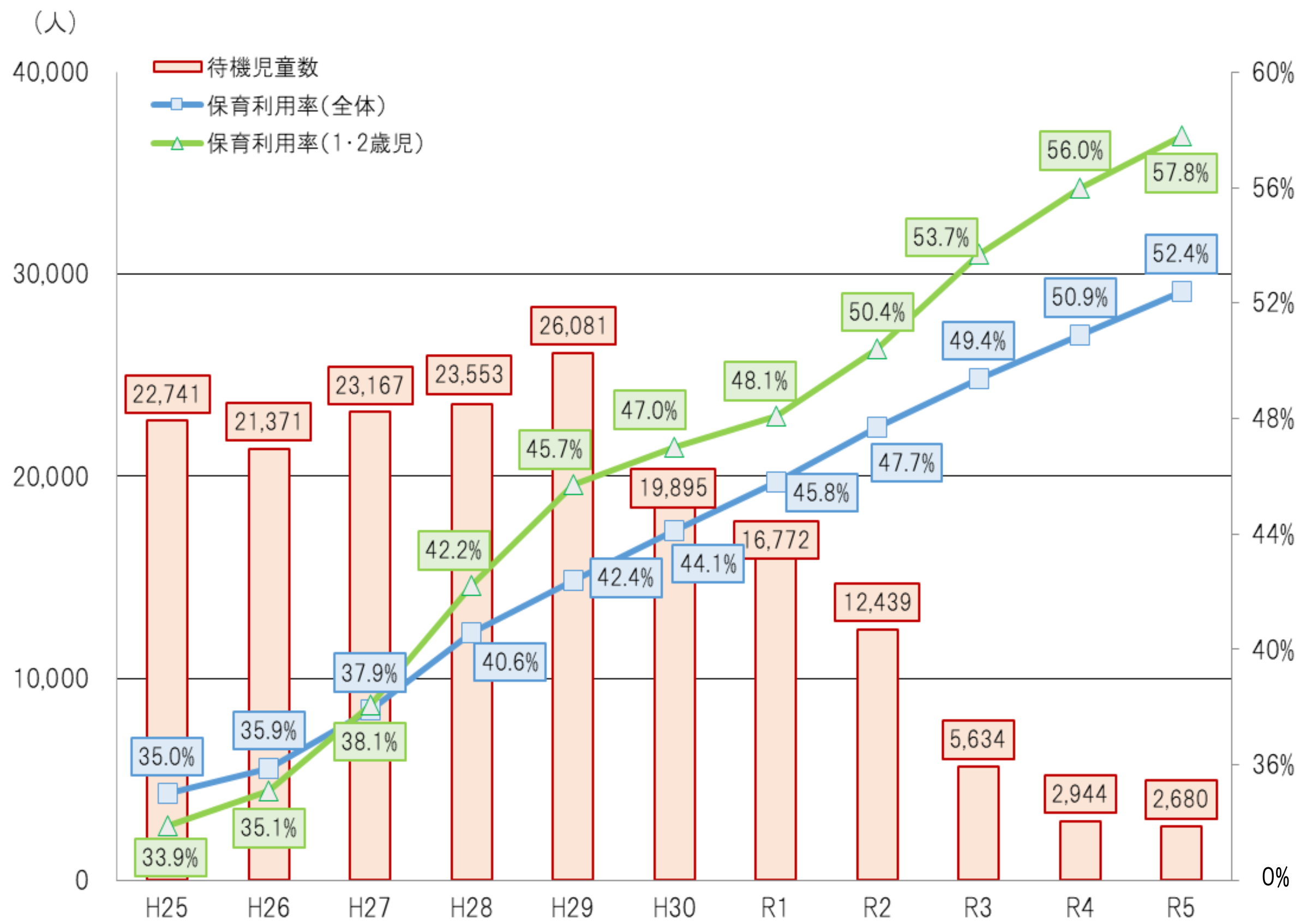
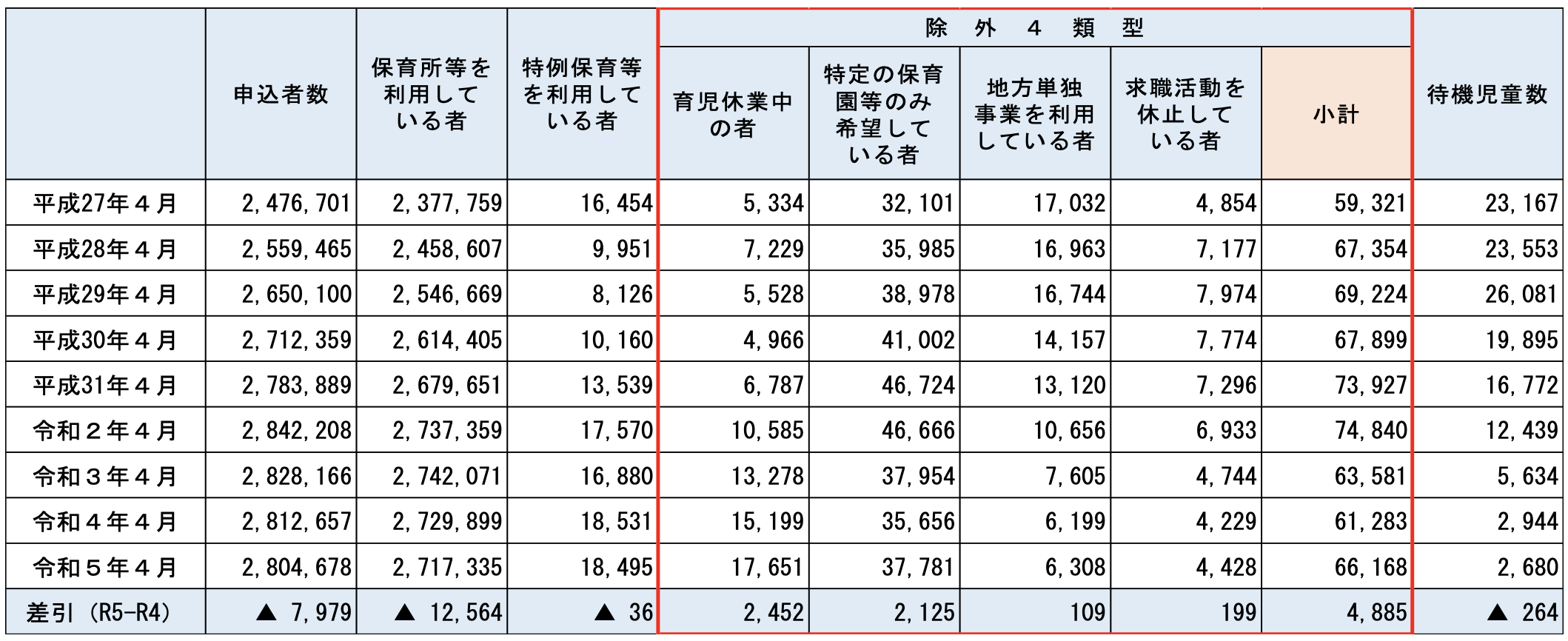
ところで待機児童の定義では、(1)育児休業中の者、(2)特定の保育園等のみ希望している者、(3)地方単独事業を利用している者、(4)求職活動を休止している者、は待機児童に含めないことになっています（「除外4類型」と呼ばれます）。しかし、これらの人数についても、待機児童の定義からは外されているものの、保育のニーズがあるにもかかわらずそれが満たされていないことから、潜在的には待機児童であると考えることもできます（「隠れ待機児童」「保留児童」などと呼ばれることもあるようです¹）。ちなみに、全国の除外4類型（以後これを「潜在的待機児童」と呼ぶことにします）の人数は、2020年の74,840年をピークに減少傾向にありましたが、直近では増加しており、2024年は71,032人でした。

準備

はじめに、今日の演習で利用するパッケージをロードしておきましょう。

# パッケージのロード
library(tidyverse)
library(readxl)
library(sf)

佐賀県内自治体の待機児童

待機児童に関する全国の待機児童の傾向はわかりました。それでは、佐賀県の状況はどのようになっているでしょうか？

演習1. 待機児童数の塗り分け地図

佐賀県内自治体の待機児童数および潜在的待機児童数を調べ、塗り分け地図を作成しましょう。図を書くためにはどのようなデータが必要でしょうか？そうです、自治体のポリゴンデータと、待機児童数のデータが必要ですね。

地図データは、佐賀県オープンデータのポリゴン（市町村別）を使いましょう。 GeoJSONファイルをダウンロードし、（ファイル名を410004saga.geojsonにして）プロジェクトのdataフォルダに移動してください。

ポリゴンデーをsf::st_read関数で読み込みます。読み込んだポリゴンデータを、sf::st_transform関数を使って、「平面直角座標系II系」に投影変換しておきます。

# 佐賀県のポリゴンデータの読み込みと投影変換
saga <- st_read("data/410004saga.geojson") |> 
  st_transform(6670)

データの内容を確認しておきましょう。市郡名と町村名が異なるデータ列に格納されていることがわかります。

# ポリゴンデータの内容確認
head(saga, 5)

Simple feature collection with 5 features and 4 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: -117268.6 ymin: -1173.744 xmax: -54075.69 ymax: 69215.3
Projected CRS: JGD2011 / Japan Plane Rectangular CS II
  KEN_NAME GST_NAME CSS_NAME KEY_CODE                       geometry
1   佐賀県   鹿島市     <NA>   412074 MULTIPOLYGON (((-82226.11 3...
2   佐賀県   唐津市     <NA>   412023 MULTIPOLYGON (((-106350 451...
3   佐賀県   神埼市     <NA>   412104 MULTIPOLYGON (((-60455.97 2...
4   佐賀県   杵島郡   江北町   414247 MULTIPOLYGON (((-78005.98 2...
5   佐賀県   多久市     <NA>   412040 MULTIPOLYGON (((-76464.8 27...

あとでこのポリゴンデータと待機児童のデータとを結合する必要があるのですが、そのためには結合する時のキーについて考えておかないといけません。最も望ましいのは、結合するデータにもKEY_CODE列が存在して、それをキーにして結合することです。しかし、実は今回利用する待機児童データにはそのようなデータ列は存在しません。なので、今回は市町名をキーにすることにします。

しかし先に見たように、このポリゴンデータは、市名と町名が異なる列に入っていますから、これを結合に使えるようするには、市名と町名をデータにもつ列を作成する必要があります。ここでは、dplyr::if_else関数を使いましょう。この関数を使って、CSS_NAME（町村名）がNA（すなわち、市）ならばGST_NAME（市郡名）を、そうでなければCSS_NAMEであるような新しいデータ列cityを追加します。

# 市町名（city）列の追加
saga <- saga |> 
  mutate(city = if_else(is.na(CSS_NAME), GST_NAME, CSS_NAME))
head(saga, 5)

Simple feature collection with 5 features and 5 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: -117268.6 ymin: -1173.744 xmax: -54075.69 ymax: 69215.3
Projected CRS: JGD2011 / Japan Plane Rectangular CS II
  KEN_NAME GST_NAME CSS_NAME KEY_CODE                       geometry   city
1   佐賀県   鹿島市     <NA>   412074 MULTIPOLYGON (((-82226.11 3... 鹿島市
2   佐賀県   唐津市     <NA>   412023 MULTIPOLYGON (((-106350 451... 唐津市
3   佐賀県   神埼市     <NA>   412104 MULTIPOLYGON (((-60455.97 2... 神埼市
4   佐賀県   杵島郡   江北町   414247 MULTIPOLYGON (((-78005.98 2... 江北町
5   佐賀県   多久市     <NA>   412040 MULTIPOLYGON (((-76464.8 27... 多久市

市町村別の待機児童数のデータは、こども家庭庁の保育所等関連状況取りまとめから入手できます。 Excelファイル「（参考）申込者の状況（令和6年4月1日）」をダウンロードし、プロジェクトのdataフォルダに移動してください。

readxl::read_excel関数で読み込みます。ここでは、Excelファイル20250122_policies_hoiku_torimatome_r6_07.xlsxについて、「申込者の状況」シートの、セルD:1537からP:1556の範囲を読み込んでいます。その際、列名は便宜的に”X1”、“X2”, …, “X12”という名前にしています。そして、dplyr::filter関数を使って、都道府県名（pref）が「佐賀県」であるデータ列だけを抽出しています。

# 待機児童データの読み込み
data <- 
  read_excel(
    path = "data/20250122_policies_hoiku_torimatome_r6_07.xlsx",
    sheet = "申込者の状況",
    range = "D1537:P1556",
    col_names = c("city", str_c("X", 1:12)),
    col_types = c("text", rep("numeric", 12))
  )
head(data, 5)

# A tibble: 5 × 13
  city      X1    X2    X3    X4    X5    X6    X7    X8    X9   X10   X11   X12
  <chr>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 佐賀市  6279  2753  2443   710   323     0     0     0     0    50     0     0
2 唐津市  3624  2386  1188     0    33     0     3     0     0     8     6     0
3 鳥栖市  1855  1503   201     2    48     6    53     0     0    42     0     0
4 多久市   490   294   194     0     2     0     0     0     0     0     0     0
5 伊万里市……  1632  1281   248     0   103     0     0     0     0     0     0     0

以降の分析では、こども家庭庁のデータのうち、「申請者数」「潜在的待機児童数」「待機児童数」のデータのみ取り出しています。ここで「潜在的待機児童数」は、先に述べて「除外4要件」に当てはまる待機者数と「待機児童数」の合計にしています。

# 待機児童データの整形
data <- data |> 
  mutate(potential = X8 + X9 + X10 + X11 + X12) |> 
  select(city, applicant = X1, waiting = X12, potential)
head(data, 5)

# A tibble: 5 × 4
  city     applicant waiting potential
  <chr>        <dbl>   <dbl>     <dbl>
1 佐賀市        6279       0        50
2 唐津市        3624       0        14
3 鳥栖市        1855       0        42
4 多久市         490       0         0
5 伊万里市      1632       0         0

これで、ポリゴンデータと統計データを結合する準備が整いました。 dplyr::left_join関数を使って結合します。

# ポリゴンデータと統計データを結合
saga <- saga |> 
  left_join(data, by = join_by(city))

それでは、これをコロプレス図にしてみましょう。ここではggplot2::ggplotを使います。まずは、待機児童の塗り分け地図です。佐賀県の待機児童は、上峰町と吉野ヶ里町に、それぞれ3人いるだけ（つまり全県で6人だけ）になっています。

# 佐賀県の市町別待機児童数
ggplot() + 
  geom_sf(aes(fill = waiting), data = saga) +
  ggrepel::geom_text_repel(
    aes(label = paste0(city, "\n", waiting, "人"), geometry = geometry),
    stat = "sf_coordinates",
    data = filter(saga, waiting > 0)
  ) + 
  scale_fill_distiller(direction = 1) +
  theme_minimal()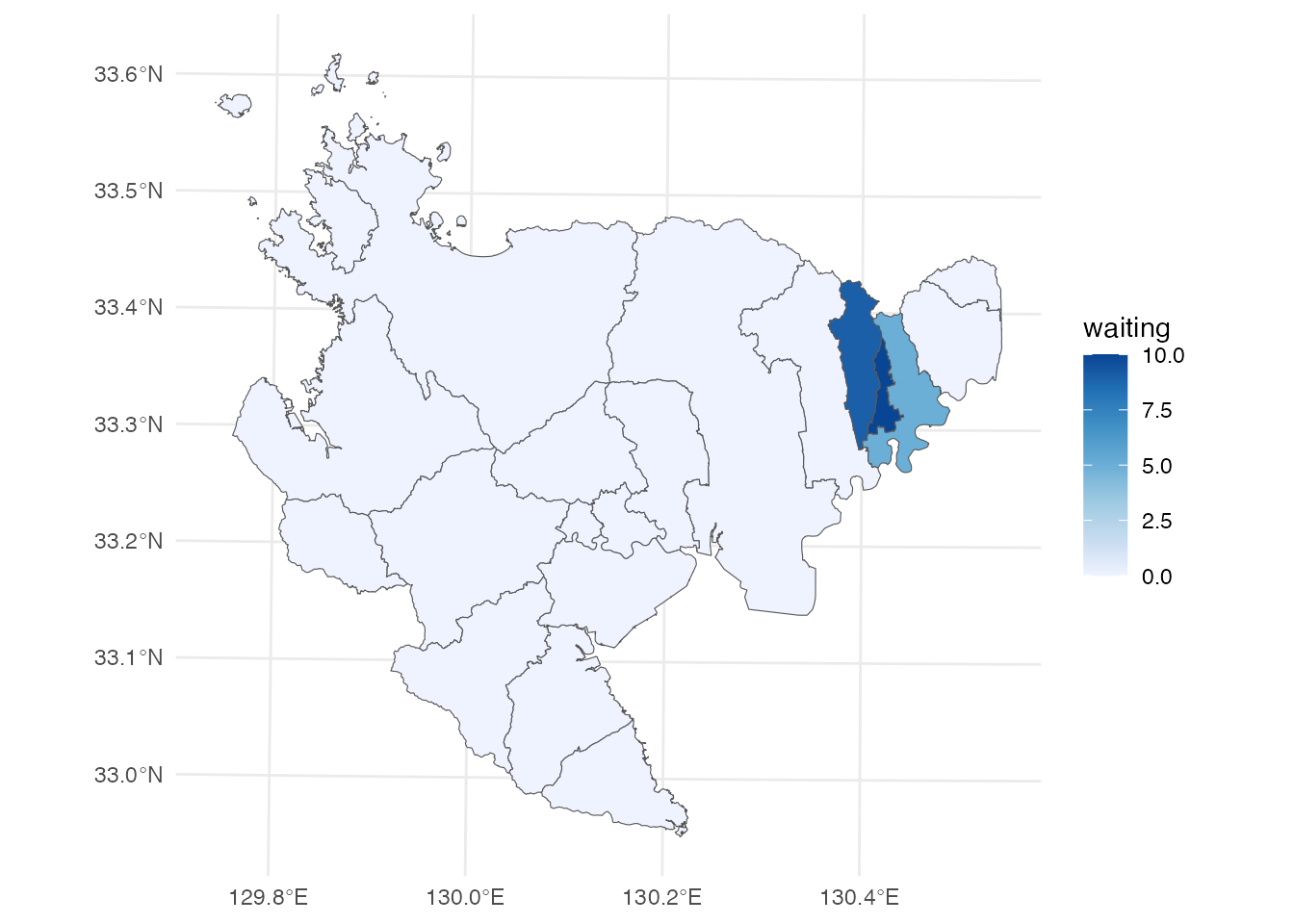

次に潜在的待機児童の塗り分け地図です。佐賀市、吉野ヶ里町、鳥栖市などで潜在的待機児童の数が多いことがわかります。

# 佐賀県の市町別潜在的待機児童数
ggplot() + 
  geom_sf(aes(fill = potential), data = saga) +
  ggrepel::geom_text_repel(
    aes(label = paste0(city, "\n", potential, "人"), geometry = geometry),
    stat = "sf_coordinates",
    data = filter(saga, potential > 0)
  ) + 
  scale_fill_distiller(direction = 1) +
  theme_minimal()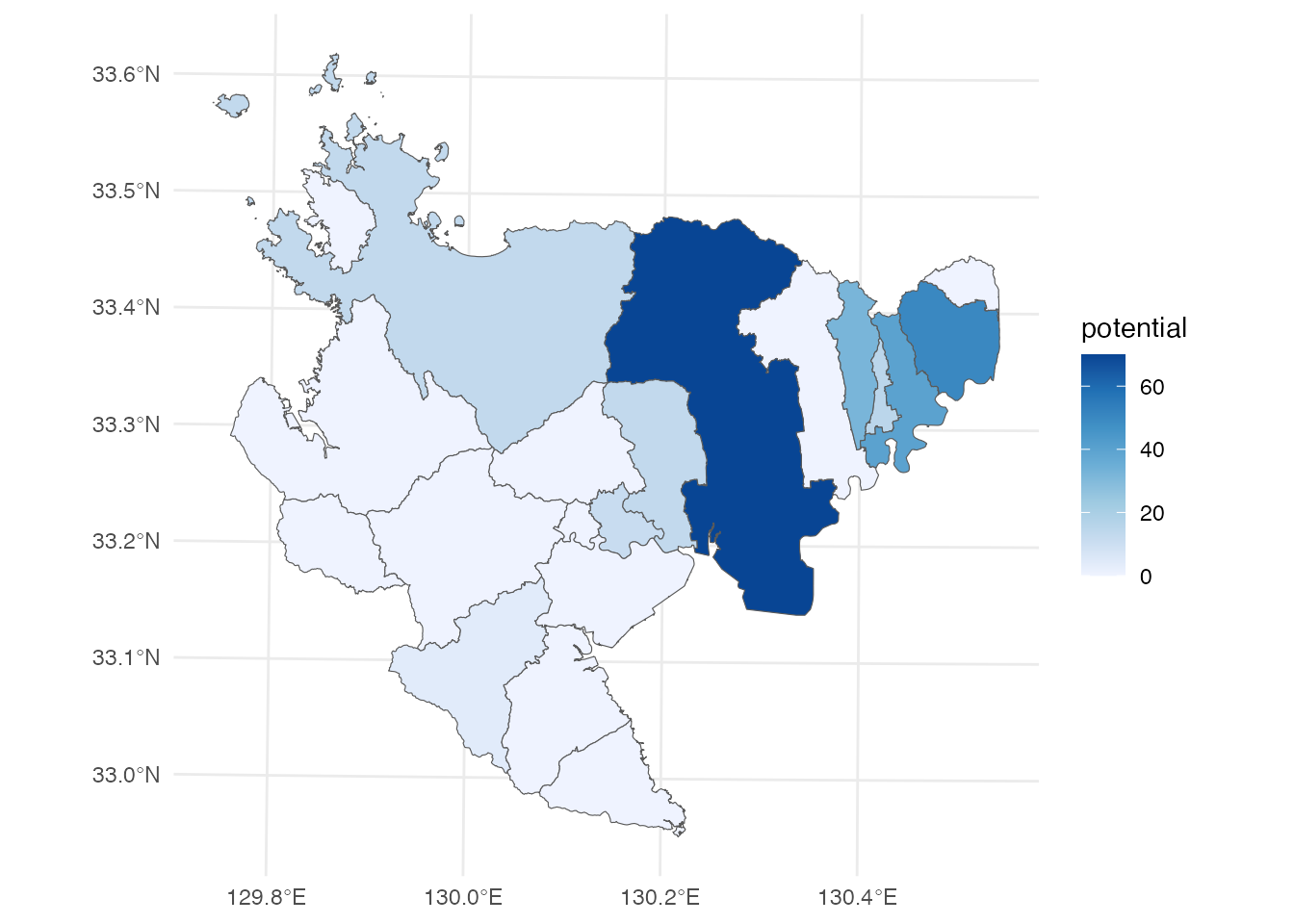

さて、これで演習1.の当初の目的は達成したのですが、せっかくデータを準備したので、もう少し掘り下げてみましょう。まず、塗り分け地図について、待機児童数そのままのデータではなく、申請者に占める待機児童の比率に直したら、結果はどのようになるでしょうか。申請者に占める潜在的待機児童の比率を地図にしてみましょう。

# 佐賀県の市町別潜在的待機児童率
saga <- saga |> 
  mutate(
    rate = potential / applicant * 100,
    label = str_glue("{city}\n{format(rate, digits = 1)}%")
  )
ggplot() + 
  geom_sf(aes(fill = rate), data = saga) +
  ggrepel::geom_text_repel(
    aes(label = label, geometry = geometry),
    stat = "sf_coordinates",
    data = filter(saga, rate > 0)
  ) + 
  scale_fill_distiller(direction = 1) +
  theme_minimal()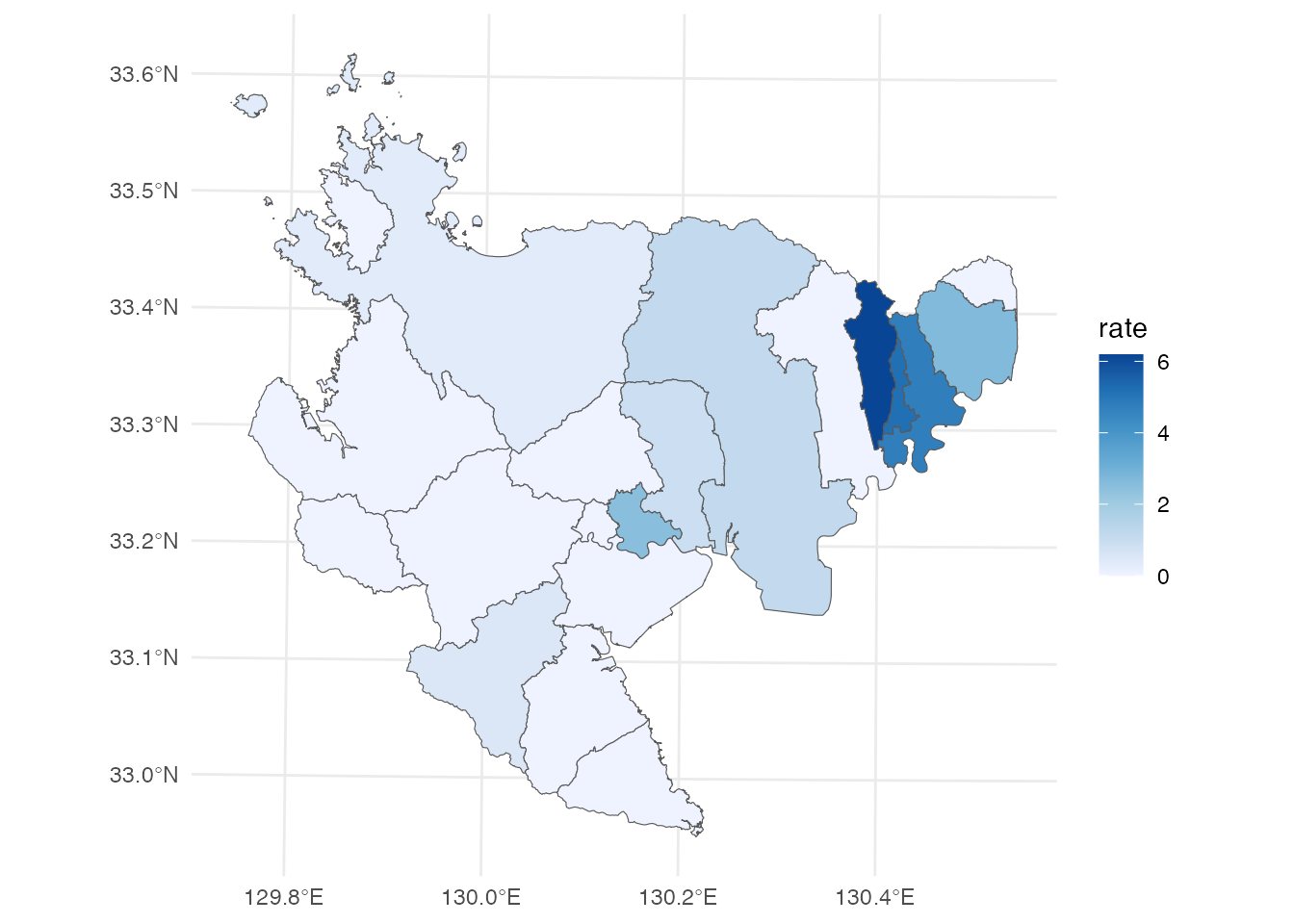

やはり佐賀県の潜在的待機児童については、東高西低の傾向があるようです。佐賀県の平均年齢が西高東低であったことを考えると、平均年齢の低い県東部で待機児童が相対的に多い、というのはそれと整合的な結果だといえるかもしれません。

つまり、そもそも県西部では保育所に対する需要が少ないのではないか、という仮説です。そこで最後に、市町別の0〜5歳人口に占める保育所等申請者の比率を可視化してみましょう。

人口データは、佐賀県統計年鑑のデータを使ってみましょう。 Excelファイル「第4章　人口及び世帯」をダウンロードし、プロジェクトのdataフォルダに移動してください。

readxl::read_excel関数で読み込みましょう。保育所を利用するのは、6歳未満の乳幼児だと考えられます。本来であれば、0〜5歳の人口が分かればいいのですが、残念ながら5歳階級の人口データしか公表されていないようなので、ここでは、0〜4歳人口に、5〜9歳人口の5分の1を加えることで、0〜5歳人口の代わりにしています。

# 市町別乳幼児人口
pop <- 
  read_excel(
    path = "data/3_112279_up_0j0s7dsy.xlsx",
    sheet = "4-7(1)",
    range = "B15:H40",
    col_names = c("city", "age04", "age59"),
    col_types = c("text", rep("skip", 3), "numeric", "skip", "numeric")
  ) |> 
  mutate(toddler = age04 + age59 / 5) |> 
  select(city, toddler)
head(pop, 5)

# A tibble: 5 × 2
  city     toddler
  <chr>      <dbl>
1 佐賀市    10384.
2 唐津市     5066 
3 鳥栖市     3656.
4 多久市      652 
5 伊万里市   2303.

dplyr::left_joinで結合しましょう。

# 乳幼児人口を結合
saga <- saga |> 
  left_join(pop, by = join_by(city))

結合したら、0〜5歳人口あたりの保育所等申請者数を塗り分け地図にしてみます。

# 佐賀県の市町別保育所等申請率
saga <- saga |> 
  mutate(rate = applicant / toddler * 100,
         label = str_glue("{city}\n{format(rate, digits = 3)}%"))
ggplot() + 
  geom_sf(aes(fill = rate), data = saga) +
  geom_sf(aes(fill = rate), data = saga) +
  ggrepel::geom_text_repel(
    aes(label = label, geometry = geometry),
    stat = "sf_coordinates",
    data = saga
  ) + 
  scale_fill_distiller(direction = 1) +
  theme_minimal()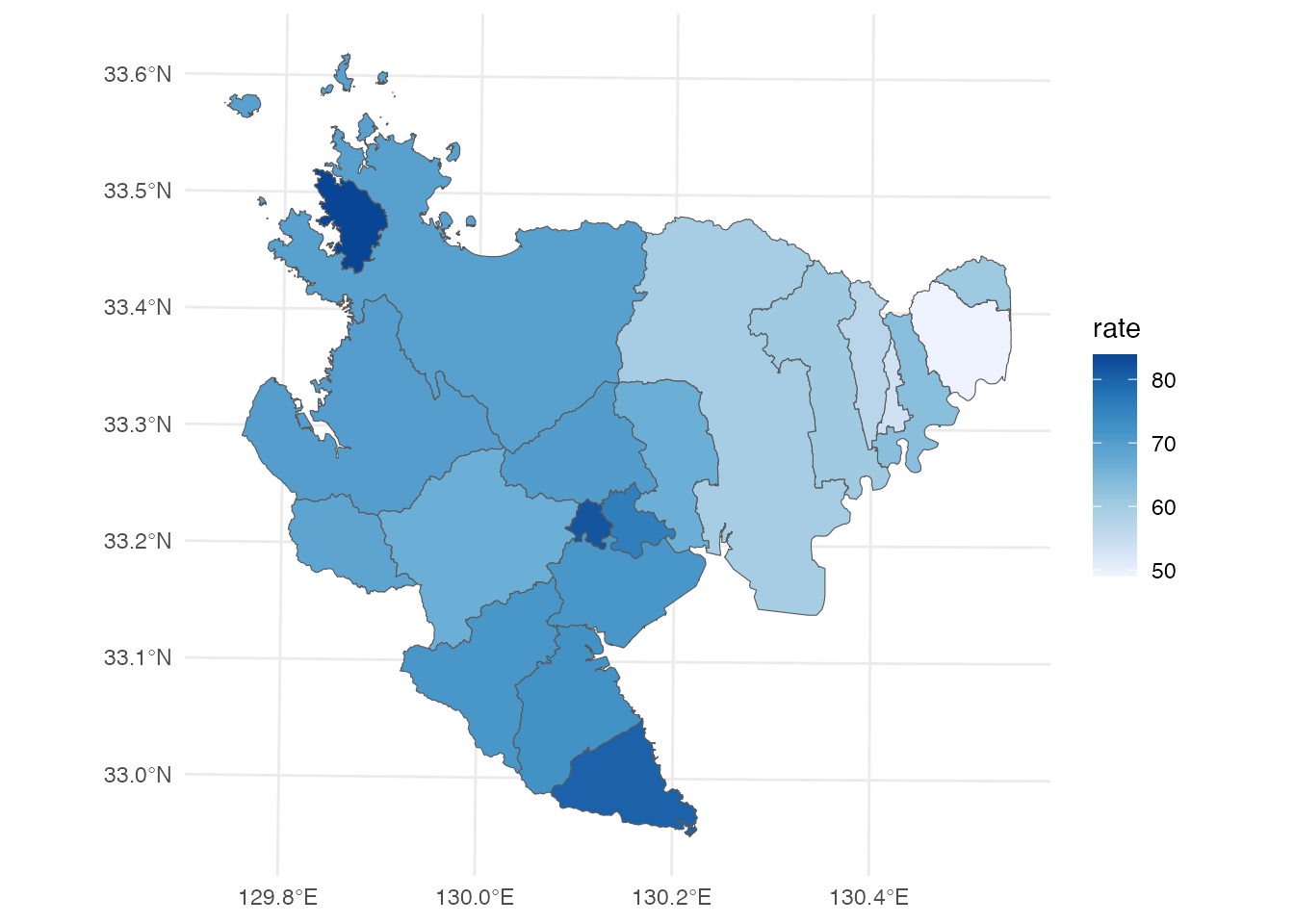

意外にも、玄海町や太良町の申請率が高く、鳥栖市が最も低いという結果になりました。（なぜこのような結果になったのか、思いつく仮説の1つは幼稚園の存在です。佐賀市や鳥栖市などの都市部では、保育所等ではなく、幼稚園に通う子供が多いのかもしれません。他にどのような仮説があるか、皆さんも考えてみてください）。

さて、佐賀県内の潜在的待機児童の大半を占めるのは、「特定の保育園等のみ希望している」児童です。これは、他の（通える範囲と見なされる²）保育園等には空きがあるのだけれど、希望する保育園等には空きがないために、通園できないでいる児童です。保育サービスの需要と供給のミスマッチが起こっていることが問題だといえます。そこで次に、佐賀市を事例として、空間的な需要と供給のミスマッチを可視化しましょう。具体的には、保育所等の立地と6歳未満人口の分布を可視化し、観察します。

演習2. 佐賀市の保育所立地と6歳未満人口分布

保育所のデータは、国土数値情報にある「福祉施設（ポイント）」を使いましょう。

佐賀県の令和3年のデータ（P14-21_41_GML.zip）をダウンロードしてください。 zipファイルを解凍し、できたP14-21_41_GMLフォルダをプロジェクトのdataフォルダに移動して下さい。

このファイルには、あらゆる福祉施設のデータが入っていますので、この中から保育所のデータだけを抜き出す必要があります。データには属性データとして、福祉施設大分類、福祉施設中分類、福祉施設小分類が入っていいますので、今回はこれを使って抜き出します。

福祉施設中分類コードを見ると、0504：保育所等、0505：地域型保育事業所、0506：認可外保育施設を抜き出せば良さそうです。属性データを使って一部のデータだけを抜き出すには、dplyr::filter関数を使います。福祉施設中分類（P14_006）が”0504”、“0505”、“0506”のいずれかであるデータだけを抽出しましょう。

# 保育所ポイントデータの読み込み
nursery <- st_read("data/P14-21_41_GML/P14-21_41.geojson") |> 
  filter(P14_006 %in% c("0504", "0505", "0506")) |> 
  st_transform(6670)

Reading layer `P14-21_41' from data source 
  `/Users/kzktmr/Documents/LectureNotes/EconomicGeography/data/P14-21_41_GML/P14-21_41.geojson' 
  using driver `GeoJSON'
Simple feature collection with 2520 features and 10 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: 129.7636 ymin: 32.96552 xmax: 130.537 ymax: 33.5962
Geodetic CRS:  JGD2011

glimpse(nursery)

Rows: 449
Columns: 11
$ P14_001  <chr> "佐賀県", "佐賀県", "佐賀県", "佐賀県", "佐賀県", "佐賀県", "佐賀県", "佐賀県", "佐賀県"…
$ P14_002  <chr> "小城市", "嬉野市", "神埼郡吉野ヶ里町", "三養基郡上峰町", "三養基郡上峰町", "杵島郡大町町", "伊万…
$ P14_003  <chr> "41208", "41209", "41327", "41345", "41345", "41423", "41205"…
$ P14_004  <chr> "牛津町牛津664", "嬉野町大字下宿乙1279", "字立野1077", "大字坊所710", "大字坊所699", …
$ P14_005  <chr> "05", "05", "05", "05", "05", "05", "05", "05", "05", "05", "…
$ P14_006  <chr> "0504", "0505", "0504", "0504", "0504", "0505", "0506", "0506…
$ P14_007  <chr> "050402", "050501", "050402", "050402", "050402", "050506", "…
$ P14_008  <chr> "牛津ルーテルこども園", "うれしのつぼみ保育園", "認定こども園　きらり", "認定こども園かみみね幼稚園", "ひ…
$ P14_009  <int> 5, 4, 5, 5, 5, 4, 5, 4, 5, 5, 5, 5, 5, 5, 5, 4, 5, 5, 3, 5, 5…
$ P14_010  <int> 1, 2, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ geometry <POINT [m]> POINT (-74531.6 27597.24), POINT (-94530.19 11738.72), …

佐賀県にある449の保育所データが登録されていることがわかります。

これを佐賀県の地図と合わせて表示てみましょう。佐賀県の地図データは、以前の講義で使った410004saga.geojsonを使いましょう（以前のプロジェクトフォルダからコピーしてください）。

自治体コードで色をつけて、地図に重ねて表示してみます。

# 保育所マップの描画
ggplot() +
  geom_sf(aes(fill = KEY_CODE), data = saga, alpha = 0.5) +
  geom_sf(aes(color = P14_003), data = nursery) +
  theme_minimal() +
  theme(legend.position = "none") # 凡例を消す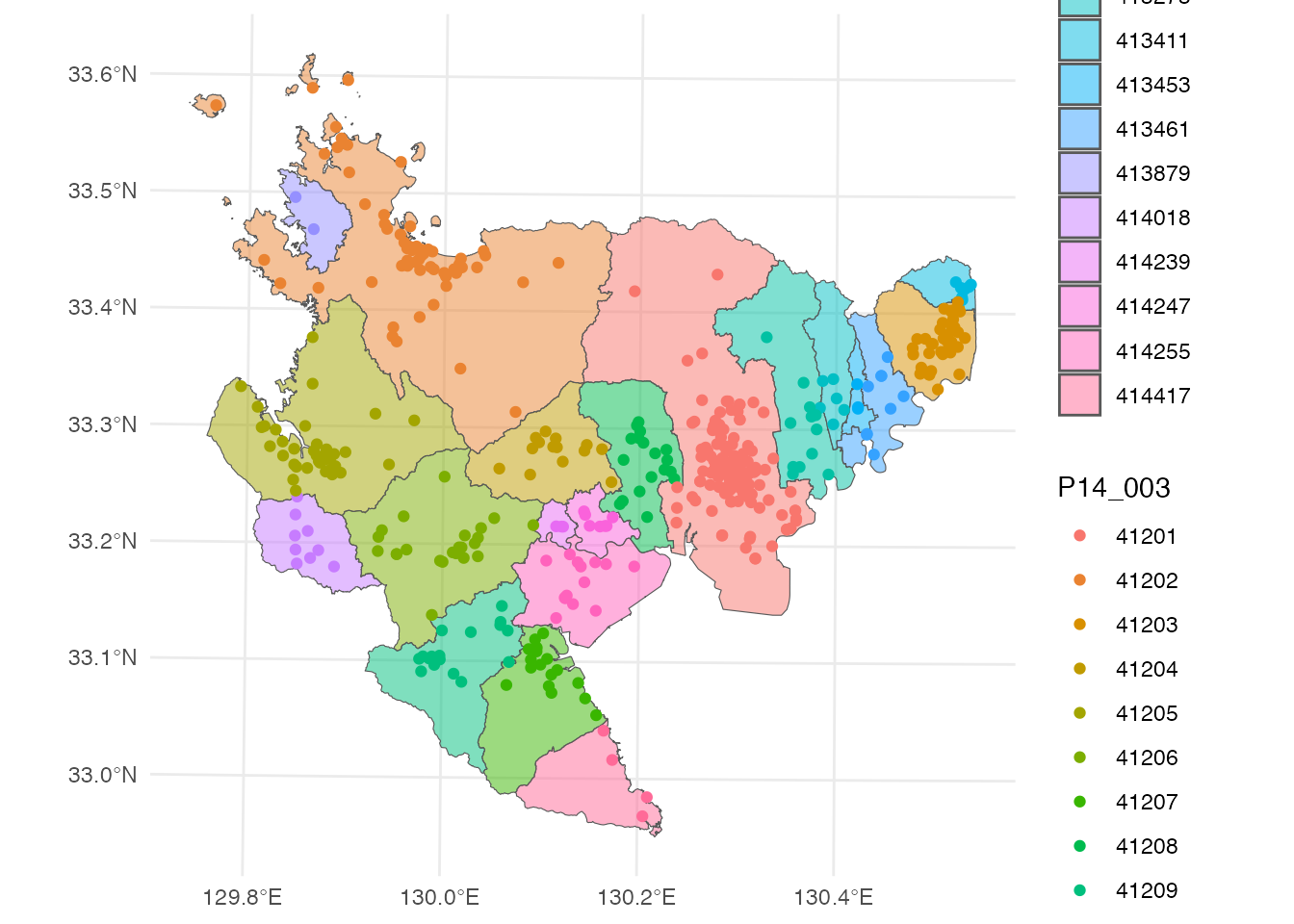

市町によって保育所の数に差がありそうですね。

では、佐賀県には20市町ありますが、それぞれの市町にいくつの保育所があるのでしょうか。 dplyr::group_byとdplyr::summariseを使って数えてみましょう。

このような時には、dplyr::count関数が便利です。

# 市町別保育所数ランキング
nursery_ranking <-
  nursery |>
  count(P14_002) |> 
  arrange(desc(n))
head(nursery_ranking, 5)

Simple feature collection with 5 features and 2 fields
Geometry type: MULTIPOINT
Dimension:     XY
Bounding box:  xmin: -114729.4 ymin: 15869.51 xmax: -43644.59 ymax: 66661.28
Projected CRS: JGD2011 / Japan Plane Rectangular CS II
   P14_002   n                       geometry
1   佐賀市 138 MULTIPOINT ((-74988.15 4660...
2   唐津市  60 MULTIPOINT ((-114729.4 6428...
3   鳥栖市  43 MULTIPOINT ((-48606.03 4121...
4 伊万里市  38 MULTIPOINT ((-112373.3 3759...
5   武雄市  24 MULTIPOINT ((-99392.73 2193...

tail(nursery_ranking, 5)

Simple feature collection with 5 features and 2 fields
Geometry type: MULTIPOINT
Dimension:     XY
Bounding box:  xmin: -107190.7 ymin: -3252.091 xmax: -53796.57 ymax: 55556.28
Projected CRS: JGD2011 / Japan Plane Rectangular CS II
            P14_002 n                       geometry
16 神埼郡吉野ヶ里町 6 MULTIPOINT ((-57407.65 3552...
17     藤津郡太良町 4 MULTIPOINT ((-77965.73 4871...
18   三養基郡上峰町 3 MULTIPOINT ((-53876.39 3777...
19     杵島郡大町町 3 MULTIPOINT ((-82455.45 2428...
20   東松浦郡玄海町 2 MULTIPOINT ((-107190.7 5555...

count関数は、引数に指定したグループごとにデータの件数を数え、nという列に件数のデータを格納します³。ここでは、自治体名を使ってグルーピングしています。これで自治体ごとの保育所数がわかりますので、dplyr::arrange関数とdplyr::desc関数を使って、データを保育所数の降順に並び替えています。

これを見ると、最も多い佐賀市には138の保育所があることがわかります。最も少ないのは玄海町で、町内の保育所数は2です。

以降の分析では、佐賀市の保育所データだけを使いますので、dplyr::filter関数を使って、データを絞り込んでおきましょう。

# 佐賀市の保育所ポイントデータ
nursery <- nursery |> filter(P14_002 == "佐賀市")
glimpse(nursery)

Rows: 138
Columns: 11
$ P14_001  <chr> "佐賀県", "佐賀県", "佐賀県", "佐賀県", "佐賀県", "佐賀県", "佐賀県", "佐賀県", "佐賀県"…
$ P14_002  <chr> "佐賀市", "佐賀市", "佐賀市", "佐賀市", "佐賀市", "佐賀市", "佐賀市", "佐賀市", "佐賀市"…
$ P14_003  <chr> "41201", "41201", "41201", "41201", "41201", "41201", "41201"…
$ P14_004  <chr> "金立町2467", "若宮1-13-17", "川副町大字早津江560-1", "兵庫町大字渕892", "長瀬町2-1…
$ P14_005  <chr> "05", "05", "05", "05", "05", "05", "05", "05", "05", "05", "…
$ P14_006  <chr> "0506", "0504", "0504", "0504", "0504", "0504", "0504", "0504…
$ P14_007  <chr> "050600", "050403", "050402", "050402", "050402", "050402", "…
$ P14_008  <chr> "金立保育園", "西九州大学附属三光保育園", "博愛の里こども園", "エミールこども園", "日新こども園(日新こど…
$ P14_009  <int> 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 4, 5, 5, 4, 4, 5, 4, 4, 5, 4, 5…
$ P14_010  <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ geometry <POINT [m]> POINT (-65032.81 35849.97), POINT (-65992.32 30151.54),…

小地域の年齢別人口のデータでは、5歳階級のものが入手できる最も細かいデータですので、先ほどと同様に、0〜4歳の人口と、5〜9歳の人口の5分の1を足し合わせたものを、保育所の潜在的な需要とみなすことにしましょう。

使うデータは、2020年国勢調査の5歳階級人口データです、e-Statからダウンロードしてください。境界データは、第5回の講義で利用したものと同じですので、第5回のプロジェクトフォルダから、「A002005212020DDSWC41201-JGD2011」フォルダをコピーして持ってきても構いません。統計データは、前回の講義で使用したものと同じですので、前回のプロジェクトフォルダから、「tblT001082C41.txt」ファイルをコピーして使っても構いません。

境界データ
- [小地域]→[国勢調査]→[2020年]→[小地域（町丁・字等）（JGD2011）]→[世界測地系緯度経度・Shapefile]→[41 佐賀県]→[41201 佐賀市]からダウンロード（ショートカット）
- 境界データ（A002005212020DDSWC41201-JGD2011.zip）を展開してできたフォルダを、プロジェクトのdataフォルダに移動
統計データ
- [国勢調査]→[2020年]→[小地域（町丁・字等）]→[年齢（５歳階級、４区分）別、男女別人口]→[41 佐賀県]からCSVファイルをダウンロード（ショートカット）
- 統計データ（tblT001082C41.zip）を展開してできたファイル（tblT001082C41.txt）を、プロジェクトのdataフォルダに移動

まずは境界データをsf::st_read関数を使って読み込みます。

# 佐賀市の小地域ポリゴンデータを読み込む
district <- 
  st_read("data/A002005212020DDSWC41201-JGD2011/r2ka41201.shp") |> 
  st_transform(6670)

Reading layer `r2ka41201' from data source 
  `/Users/kzktmr/Documents/LectureNotes/EconomicGeography/data/A002005212020DDSWC41201-JGD2011/r2ka41201.shp' 
  using driver `ESRI Shapefile'
Simple feature collection with 484 features and 29 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 130.1393 ymin: 33.14109 xmax: 130.3794 ymax: 33.48151
Geodetic CRS:  JGD2011

次に、統計データをreadr::read_csv関数を使って読み込みます。前回と同様、ファイルをヘッダ部分とデータ部分に分けて、read_csv関数を2回使って読み込みます。

まずは、先頭行だけ読み込んで、列名の文字列ベクトルを作ります。

# 佐賀市の小地域年齢階級別人口データ（ヘッダ部）
col_names <- 
  read_csv("data/tblT001082C41.txt", col_types = "c", 
           col_names = FALSE, n_max = 1, 
           locale = locale(encoding = "cp932")) |> 
  as.character()

次に、列名の文字列ベクトルを利用して、CSVファイルを読み込みます。ここでは、空白「」と欠損値「-」および秘匿データ（X）をNAにするように設定しています。また、文字コードを指定して、日本語が正しく読み込まれるようにしておきます。

# 佐賀市の小地域年齢階級別人口データの読み込み
population <- 
  read_csv("data/tblT001082C41.txt", skip = 2,
           na = c("", "-", "X"), col_names = col_names,
           locale = locale(encoding = "cp932"))

Rows: 2567 Columns: 67
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr  (4): CITYNAME, NAME, HTKSAKI, GASSAN
dbl (63): KEY_CODE, HYOSYO, HTKSYORI, T001082001, T001082002, T001082003, T0...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

たくさんのデータがありますが、このうち0〜4歳人口と5〜9歳人口のデータを使って、0〜5歳人口を推計します。また同時に、列の名前をわかりやすく「toddler」にしておきます（さらに、このあとの演習3. で利用するために、65歳以上人口の列も「elderly」という列名で取り出しておきます）。また、KEY_CODEを文字列型に変更しているのは、left_joinのキーにするときに、saga_cityのKEY_CODEとデータ型が違うとエラーになるので、その対策です。

# 佐賀市の小地域乳幼児人口と高齢者人口
population <- population |> 
  filter(CITYNAME == "佐賀市") |> 
  mutate(KEY_CODE = as.character(KEY_CODE),
         toddler = T001082002 + T001082003 / 5,
         elderly = T001082019) |> 
  select(KEY_CODE, toddler, elderly)
head(population, 5)

# A tibble: 5 × 3
  KEY_CODE    toddler elderly
  <chr>         <dbl>   <dbl>
1 41201       11085.    64802
2 412010010     128.      349
3 41201001001    15.4      73
4 41201001002    61.2     132
5 41201001003    51.8     144

KEY_CODEをキーにして、境界データに統計データを結合します。 dplyr::left_join関数を使います。また、キーを指定するのに、dplyr::join_by関数を使っています。

# ポリゴンデータに乳幼児人口と高齢者人口を結合
district <- district |> 
  left_join(population, by = join_by(KEY_CODE))
head(district)

Simple feature collection with 6 features and 31 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: -65669.76 ymin: 28615.66 xmax: -64122.89 ymax: 30085.38
Projected CRS: JGD2011 / Japan Plane Rectangular CS II
     KEY_CODE PREF CITY S_AREA PREF_NAME CITY_NAME         S_NAME KIGO_E HCODE
1 41201001001   41  201 001001    佐賀県    佐賀市 駅前中央一丁目   <NA>  8101
2 41201001002   41  201 001002    佐賀県    佐賀市 駅前中央二丁目   <NA>  8101
3 41201001003   41  201 001003    佐賀県    佐賀市 駅前中央三丁目   <NA>  8101
4 41201002001   41  201 002001    佐賀県    佐賀市     大財一丁目   <NA>  8101
5 41201002002   41  201 002002    佐賀県    佐賀市     大財二丁目   <NA>  8101
6 41201002003   41  201 002003    佐賀県    佐賀市     大財三丁目   <NA>  8101
       AREA PERIMETER R2KAxx R2KAxx_ID KIHON1 DUMMY1 KIHON2  KEYCODE1  KEYCODE2
1 147281.68  1528.456      1         0   0010      -     01 201001001 201001001
2 108748.65  1371.930      2         1   0010      -     02 201001002 201001002
3 144423.54  1875.425      3         2   0010      -     03 201001003 201001003
4  74548.31  1150.161      4         3   0020      -     01 201002001 201002001
5 137859.16  1900.060      5         4   0020      -     02 201002002 201002002
6  78556.12  1455.806      6         5   0020      -     03 201002003 201002003
  AREA_MAX_F KIGO_D N_KEN N_CITY KIGO_I KBSUM JINKO SETAI   X_CODE   Y_CODE
1          M   <NA>  <NA>   <NA>   <NA>    16   583   378 130.2978 33.26336
2          M   <NA>  <NA>   <NA>   <NA>    14  1081   576 130.2995 33.26637
3          M   <NA>  <NA>   <NA>   <NA>    19   832   432 130.3041 33.26694
4          M   <NA>  <NA>   <NA>   <NA>    11   337   202 130.3027 33.25728
5          M   <NA>  <NA>   <NA>   <NA>    10   797   413 130.3083 33.25828
6          M   <NA>  <NA>   <NA>   <NA>    14   626   357 130.3031 33.26060
   KCODE1 toddler elderly                       geometry
1 0010-01    15.4      73 POLYGON ((-65206.16 29463.9...
2 0010-02    61.2     132 POLYGON ((-65394.07 29604.2...
3 0010-03    51.8     144 POLYGON ((-64853.05 29908.1...
4 0020-01    12.8      93 POLYGON ((-64797.21 28877.8...
5 0020-02    35.6     200 POLYGON ((-64173.43 28781.4...
6 0020-03    21.4     129 POLYGON ((-64859.3 29155.46...

0〜5歳人口と保育所の分布を重ねて表示してみましょう。

# 佐賀市の乳幼児人口と保育所の分布
ggplot() + 
  geom_sf(aes(fill = toddler), data = district) +
  geom_sf(data = nursery, alpha = 0.5) +
  scale_fill_distiller(direction = 1) +
  theme_minimal()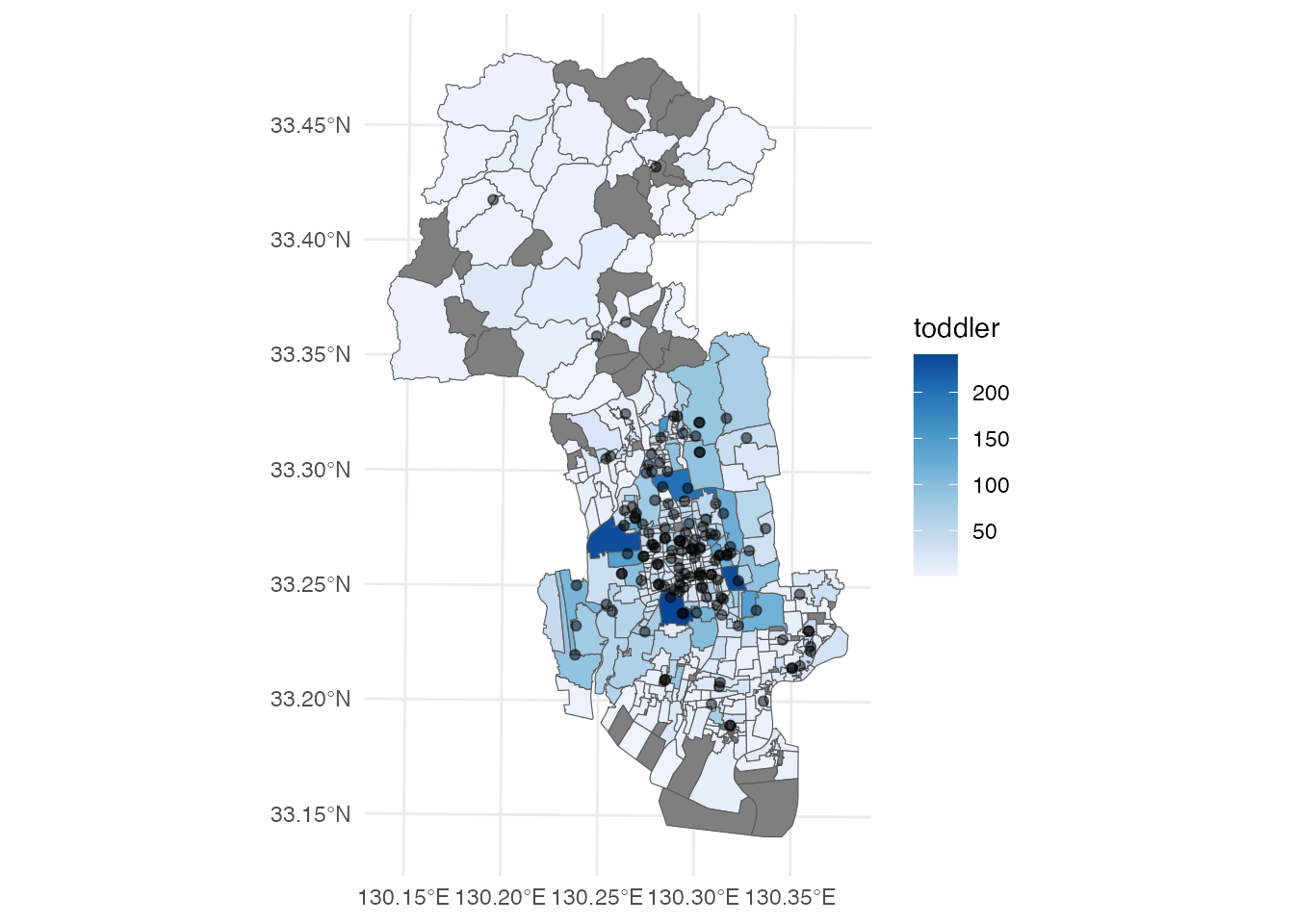

さて、ここから、空間的な需要と供給のミスマッチを議論したいのですが、需要側のデータである保育園等利用申請者数の小地域データも、供給側である保育所等の定員のデータもありませんので、ここでは簡易的な分析になってしまいますが、保育所等と居住地との距離を用いた分析をしてみましょう。

まず、居住地から距離1,000 m以内に保育所が1つもない地区を可視化してみましょう。 sf::st_nearest_feature関数を使って、それぞれの小地域から最も近い保育所を特定しています。そして、sf::st_distance関数を使って、それぞれの小地域とそこから最も近い保育所等の距離を計算しています。最後に、nursery1というデータ列を作成しています。最寄りの保育所までの距離が1,000 mを超えるかどうかという論理型データ（TRUEまたはFALSEのどちらかの値を持つ）になっています。

# 各小地域から最も近い保育所までの距離
nearest_nursery <- st_nearest_feature(district, nursery)
nearest_nursery_dist <-
  st_distance(district, nursery[nearest_nursery,], by_element = TRUE) |> 
  units::drop_units()
district <- district |> 
  mutate(nursery1 = nearest_nursery_dist > 1000)
table(district$nursery1)


FALSE  TRUE 
  405    79

全部で484ある小地域のうち、最寄り保育所までの距離が1,000 mを超える地域は79あるようです。

最寄り保育所までの距離が1,000mを超える地域をどのような場所にあるのか、地図にしてみましょう。

# 最寄り保育所までの距離が1,000mを超える地域の可視化
ggplot() +
  geom_sf(aes(fill = nursery1), data = district) +
  theme_minimal()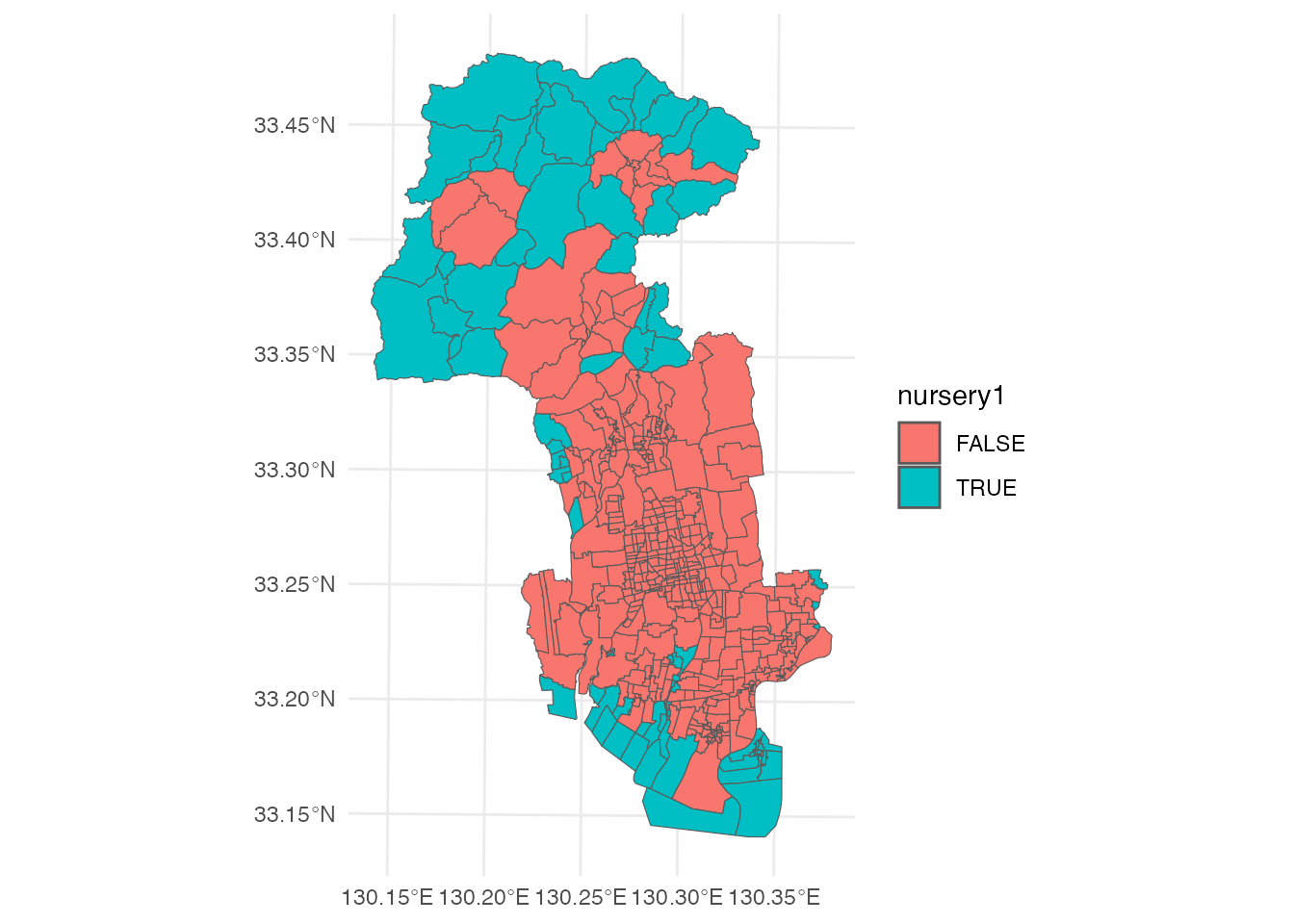

また、市全体の0〜6歳人口のうち、最寄り保育所までの距離が1,000 mを超える地域に住む子どもの比率は、以下のようにして計算できます。

# 最寄り保育所までの距離が1,000mを超える児童の比率
sum(district$toddler * district$nursery1, na.rm = TRUE) / sum(district$toddler, na.rm = TRUE) * 100

[1] 3.585765

全体のおよそ3.6％という結果になりました。この数字は、みなさんの予想と比べてどうだったでしょうか。

さて、潜在的待機児童の大半は、通園可能と考えられる範囲に保育所等があるにも関わらず、何らかの理由によって待機している児童でした。このような潜在的待機児童を減らすためには、何が必要となるのでしょうか。最も必要となることの1つは、保育所等の選択肢を増やすことでしょう。通園可能な保育所が0であるよりも1つでもあったほうがいいですし、通園可能な保育所等が1つしかないよりも2つ以上あったほうがより良いといえます。

そこで次に、居住地から、距離1,000 m以内の保育所が2箇所未満である（1つもない、もしくは1つしかない）地区を可視化してみましょう。これを実現する方法は、いくつか考えられますが、ここでは、地区と保育所の距離行列を計算した後、地区ごとに、そこから距離1,000 mの範囲にある保育所等の数を数えることにします。

距離行列は、sf::st_distance関数を使って計算できます。これを、距離が1,000 m以下かどうかを表す論理行列に変換し、rowSums関数でその行方向の和を計算しています（論理型の値は、TRUE=1、FALSE=0として計算できますので、行和を計算することで、TRUEの個数をカウントすることができます）。最後に、この行和（つまり、距離1,000 m以下にある保育所等の数）が2未満かどうかという論理型データをnursery2として新しいデータ列にして追加しています。

# 2番目に近い保育所までの距離
distance_matrix <- st_distance(district, nursery) |> 
  units::drop_units()
n_nursery <- rowSums(distance_matrix <= 1000)
district <- district |> 
  mutate(nursery2 = n_nursery < 2)

結果を塗り分け地図にしてみましょう。

# 2番目に近い保育所までの距離が1,000mを超える地域
ggplot() +
  geom_sf(aes(fill = nursery2), data = district) +
  theme_minimal()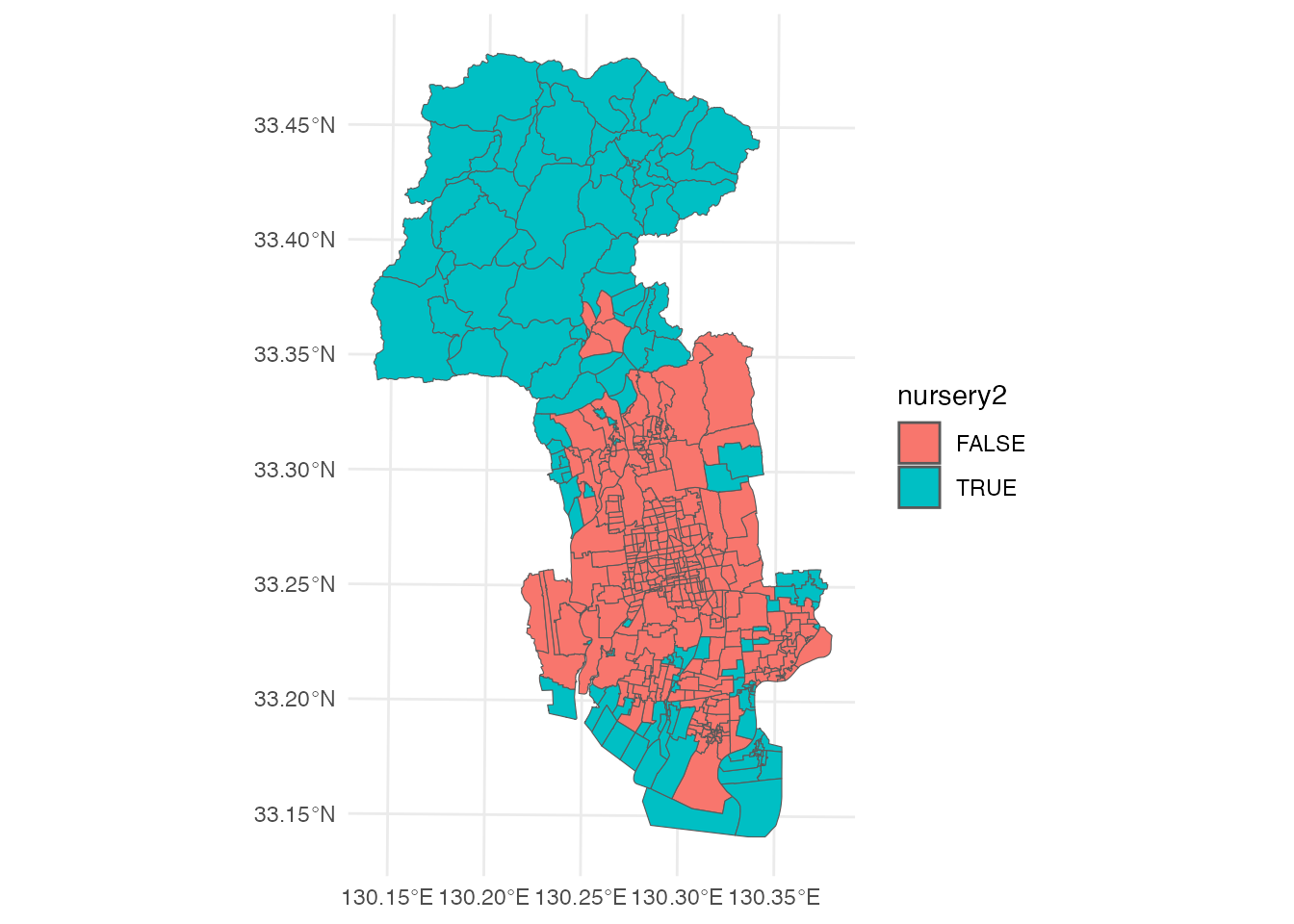

先ほどと比べて、TRUEである地区、すなわち保育所までのアクセス性が悪いと評価される地区が増えていることがわかると思います。 0〜5最人口に占める比率も計算してみましょう。

# 2番目に近い保育所までの距離が1,000mを超える児童の比率
sum(district$toddler * district$nursery2, na.rm = TRUE) / sum(district$toddler, na.rm = TRUE) * 100

[1] 7.064822

先ほどの最も近い保育所までの距離を考えた時よりも、比率が大きくなっていることが確認できました。

このように、\(n\)番目に近い施設までの距離を考えることは重要です。特に、近年多発する自然災害など、不確実性を考慮した際には、最寄りの施設が利用できなくなった時のバックアップをどうするかを考えておく必要があります。潜在的待機児童の、何らかの理由によって最寄りの保育所等に通園できないという問題も、同じ枠組みで考えることができると思います。

佐賀市のバスアクセス

佐賀市内には、路線バス事業者が4社バスを走らせていますし、市北部ではコミュニティバスも走っています。佐賀駅バスセンターはとてもきれいて使いやすいですし、バスセンターでの他社バス間の乗り継ぎ割引という制度は、全国的にみてもあまり例はないのではないかと思います。

私も毎日、佐賀駅バスセンターから佐賀大学までバスに乗ってきますが、バスはいつも混んでいます。学生と高齢者の利用が多いと感じます。

そこで、次のテーマとして、佐賀市内のバスアクセスを取り上げることにします。

演習3. 佐賀市内のバス停分布と高齢人口分布

バス停のデータは、国土数値情報からダウンロードしてください。バス停（ポイント）データと、バスルート（ライン）データが別々のファイルになっています。

バス停留所データから、佐賀県の2022年度のShapeFile形式・GeoJSON形式のデータ（P11-22_41_SHP.zip）をダウンロードします。
バスルートデータから、佐賀県の2022年度のShapeFile形式・GeoJSON形式のデータ（N07-22_41_SHP.zip）をダウンロードします。

ダウンロードしたら、ダウンロードフォルダで展開し、できたフォルダごと、プロジェクトのdataフォルダに移動してください。

sf::st_read関数で読み込みます。平面直角座標系II系に投影変換しておきましょう。

# バスデータの読み込み
stops <- st_read('data/P11-22_41_SHP/P11-22_41.geojson') |> 
  st_transform(6670)

Reading layer `P11-22_41' from data source 
  `/Users/kzktmr/Documents/LectureNotes/EconomicGeography/data/P11-22_41_SHP/P11-22_41.geojson' 
  using driver `GeoJSON'
Simple feature collection with 3080 features and 73 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: 129.7615 ymin: 32.95459 xmax: 130.5412 ymax: 33.55822
Geodetic CRS:  JGD2011

route <- st_read('data/N07-22_41_SHP/N07-22_41.geojson') |> 
  st_transform(6670)

Reading layer `N07-22_41' from data source 
  `/Users/kzktmr/Documents/LectureNotes/EconomicGeography/data/N07-22_41_SHP/N07-22_41.geojson' 
  using driver `GeoJSON'
Simple feature collection with 4021 features and 2 fields
Geometry type: LINESTRING
Dimension:     XY
Bounding box:  xmin: 129.7592 ymin: 32.95459 xmax: 130.5418 ymax: 33.55822
Geodetic CRS:  JGD2011

ggplotを使って、佐賀市内のバス路線図を描いてみましょう。 sf::st_filter関数を使って、佐賀県のバス停とバスルートデータから、佐賀市内にあるものだけを抽出します。 ggplotを使って、地図にします。「バス事業者名」で色を変えるように設定しています。

# 佐賀市内のバス路線図の描画
saga_city <- saga |> filter(GST_NAME == '佐賀市')
saga_stops <- stops |> st_filter(saga_city)
saga_route <- route |> st_filter(saga_city)
ggplot() +
  geom_sf(data = saga_city) +
  geom_sf(aes(color = P11_002), data = saga_stops, alpha = 0.5) +
  geom_sf(aes(color = N07_001), data = saga_route) +
  theme_minimal()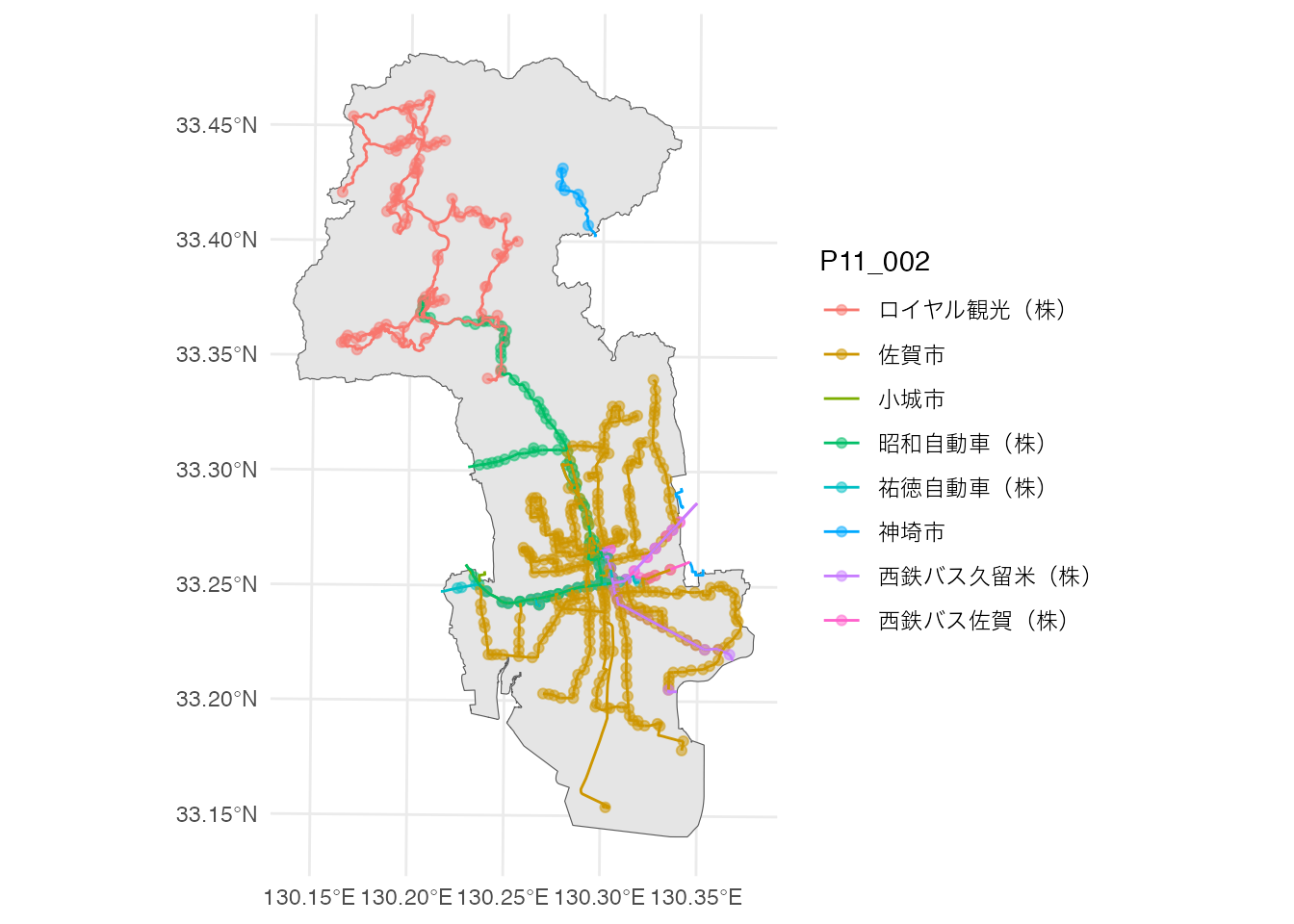

神埼市のコミュニティバスのバス停が、一部佐賀市内にあるようですね。神埼市のバスを除いた、それ以外のバス停を地図にしてみます。このデータを分析に使うことにしましょう。

# 佐賀市内のバス停地図の描画
saga_stops <- saga_stops |> 
  filter(P11_002 != '神埼市')
ggplot() +
  geom_sf(data = saga_city) +
  geom_sf(aes(color = P11_002), data = saga_stops, alpha = 0.5) +
  theme_minimal()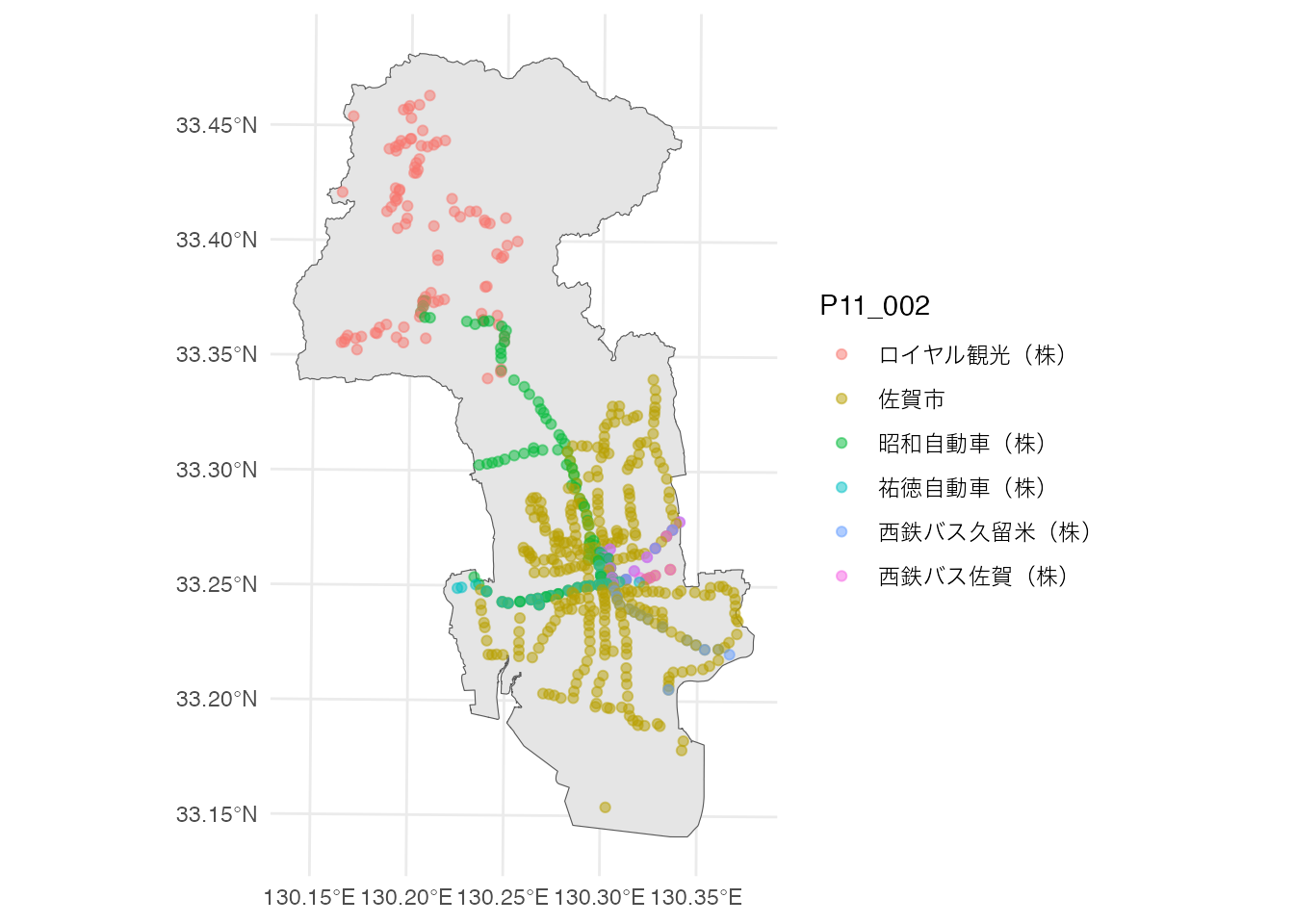

次は高齢人口分布です。これは、演習2. で使った国勢調査の小地域人口データを使いましょう。先ほど作ったdistrictデータに、65歳以上人口のelderly列があります。 ggplotを使って、65歳以上人口の塗り分け地図を描いてみます。

# 高齢者地図の描画
ggplot() +
  geom_sf(aes(fill = elderly), data = district) +
  scale_fill_distiller(direction = 1) +
  theme_minimal()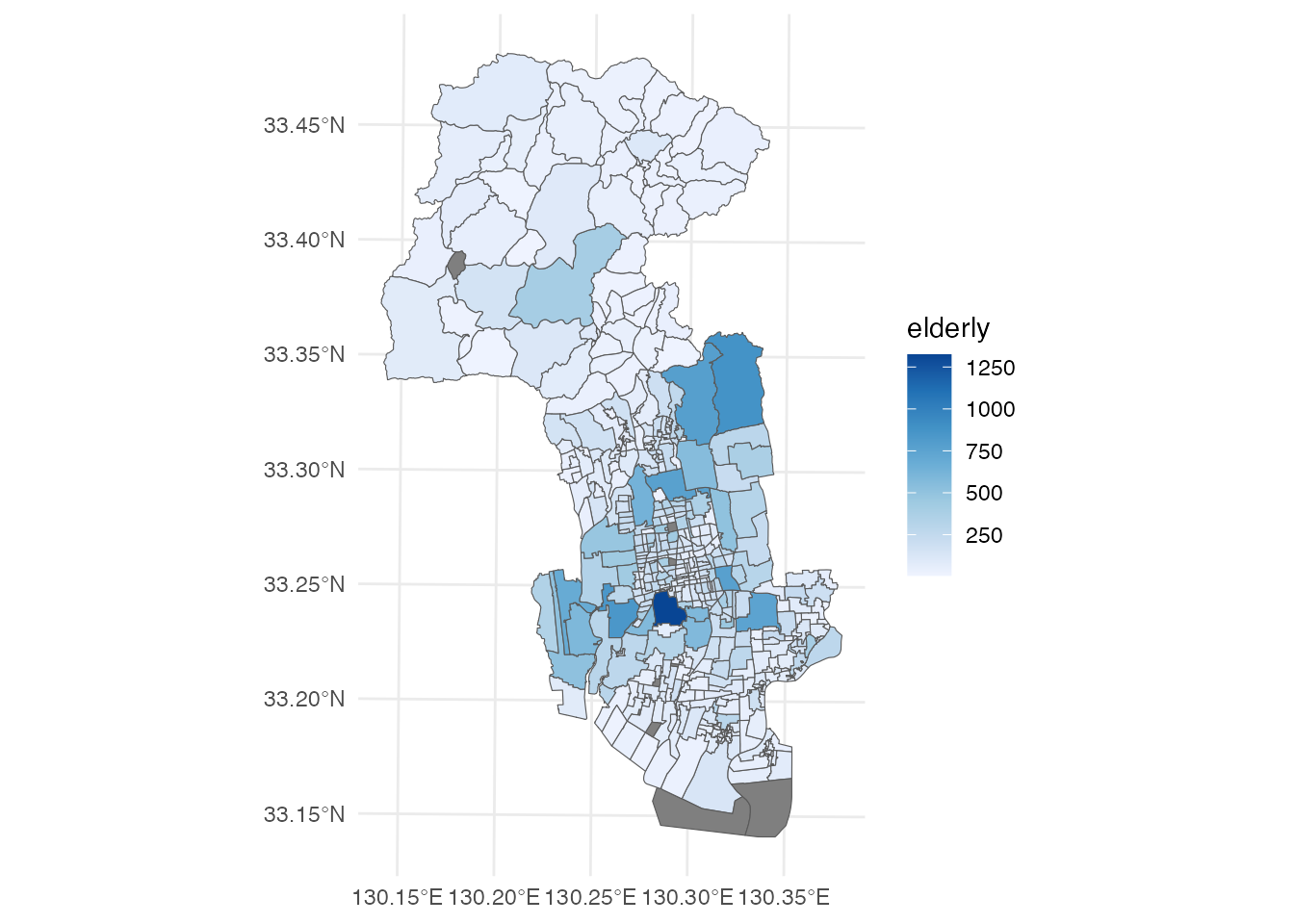

これと、先ほどのバス停データを重ねてみましょう。

# 高齢者分布とバス停位置
ggplot() +
  geom_sf(aes(fill = elderly), data = district) +
  geom_sf(data = saga_stops, color = 'blue', alpha = 0.5) +
  scale_fill_distiller(direction = 1) +
  theme_minimal()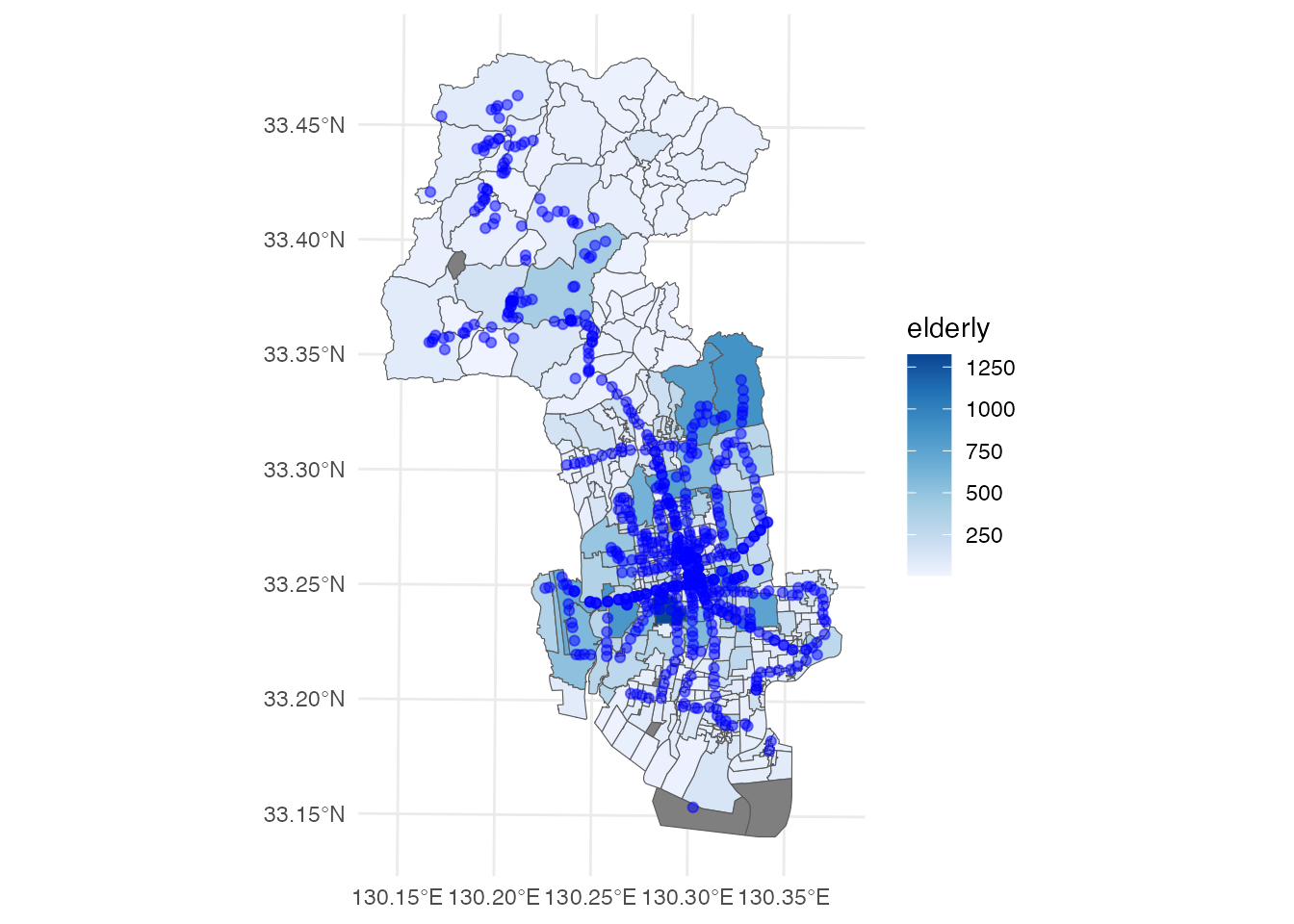

さて、このバス停の位置と高齢者の分布を分析したいわけですが、先ほどの保育所の分析とは違うツールを使いましょう。ここでは、バッファーを使ってバス停からの距離と人口分布との関係を分析します。 sf::st_buffer関数を使って、バス停から500 mのバッファーを作成しています。各バス停から500 mの円形領域が作成されますので、これにsf::st_union関数を適用して、1つの領域に集計しています。

# バス停から500mのバッファー
buffer <- saga_stops |> st_buffer(dist = 500) |> st_union()
ggplot() +
  geom_sf(aes(fill = elderly), data = district) +
  geom_sf(data = buffer, color = 'red', alpha = 0.5) +
  scale_fill_distiller(direction = 1) +
  theme_minimal()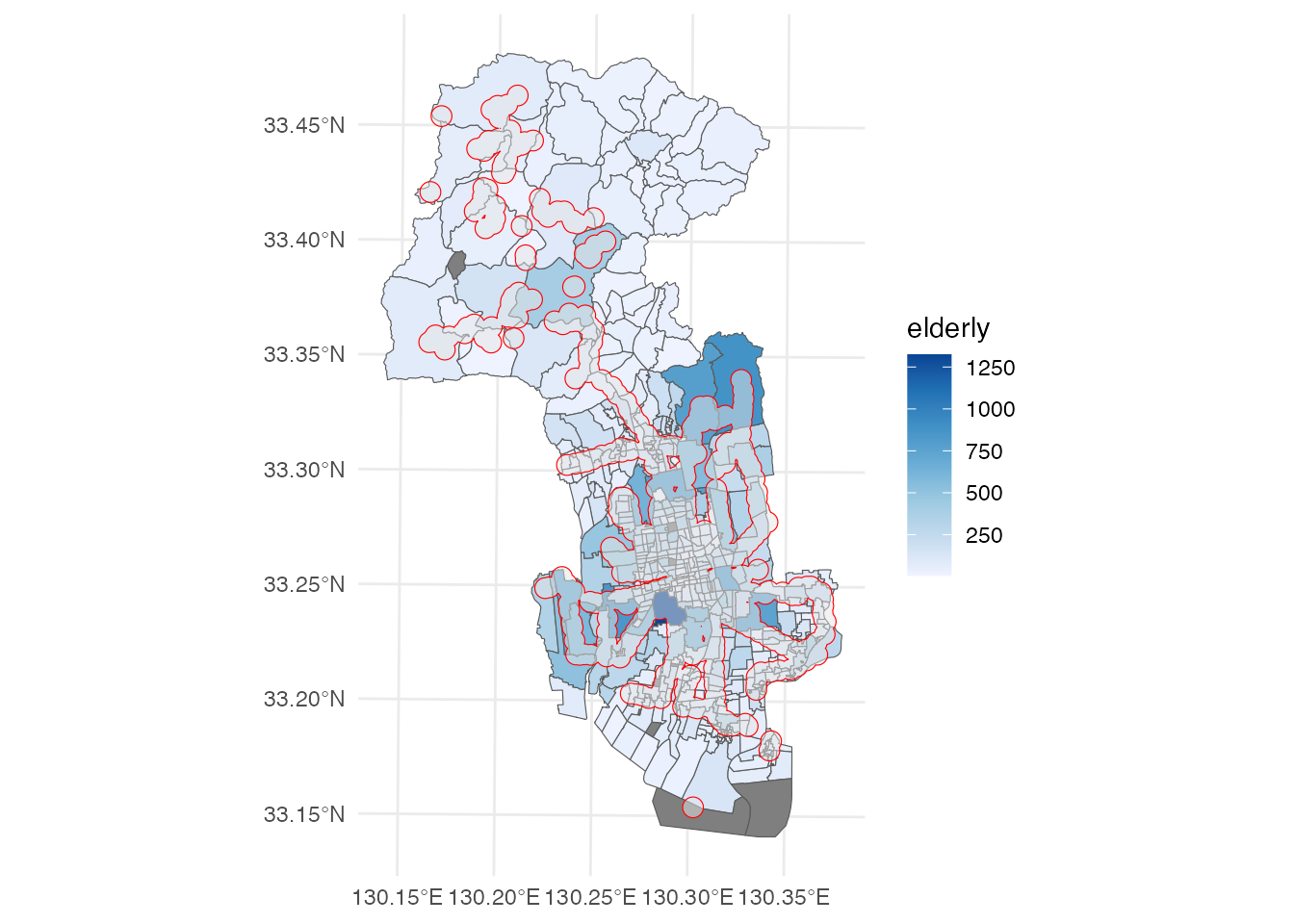

このバッファー領域に含まれる高齢者人口を集計しましょう。色々な方法があると思いますが、ここでは面積按分によって各小地域の人口を、バッファーに含まれる部分と含まれない部分とに分けてみましょう。

はじめに、小地域の面積を計算しています。国勢調査の境界データには、面積データ（AREA）が入っているのですが、ここでは面積按分する際に結果を整合させるために、同じ方法で計測した面積を使いたいために、あえて面積を計算しています。

sf::sf_intersection関数を使って、小地域領域とバス停のバッファー領域の共通部分を取り出しています。含まれる部分を取り出しています。

# 小地域とバス停バッファーの交差
district <- district |> 
  mutate(area = st_area(district))
intersect <- district |> 
  st_intersection(buffer)

Warning: attribute variables are assumed to be spatially constant throughout
all geometries

ggplot() +
  geom_sf(data = saga_city) +
  geom_sf(aes(fill = elderly), data = intersect) +
  scale_fill_distiller(direction = 1) +
  theme_minimal()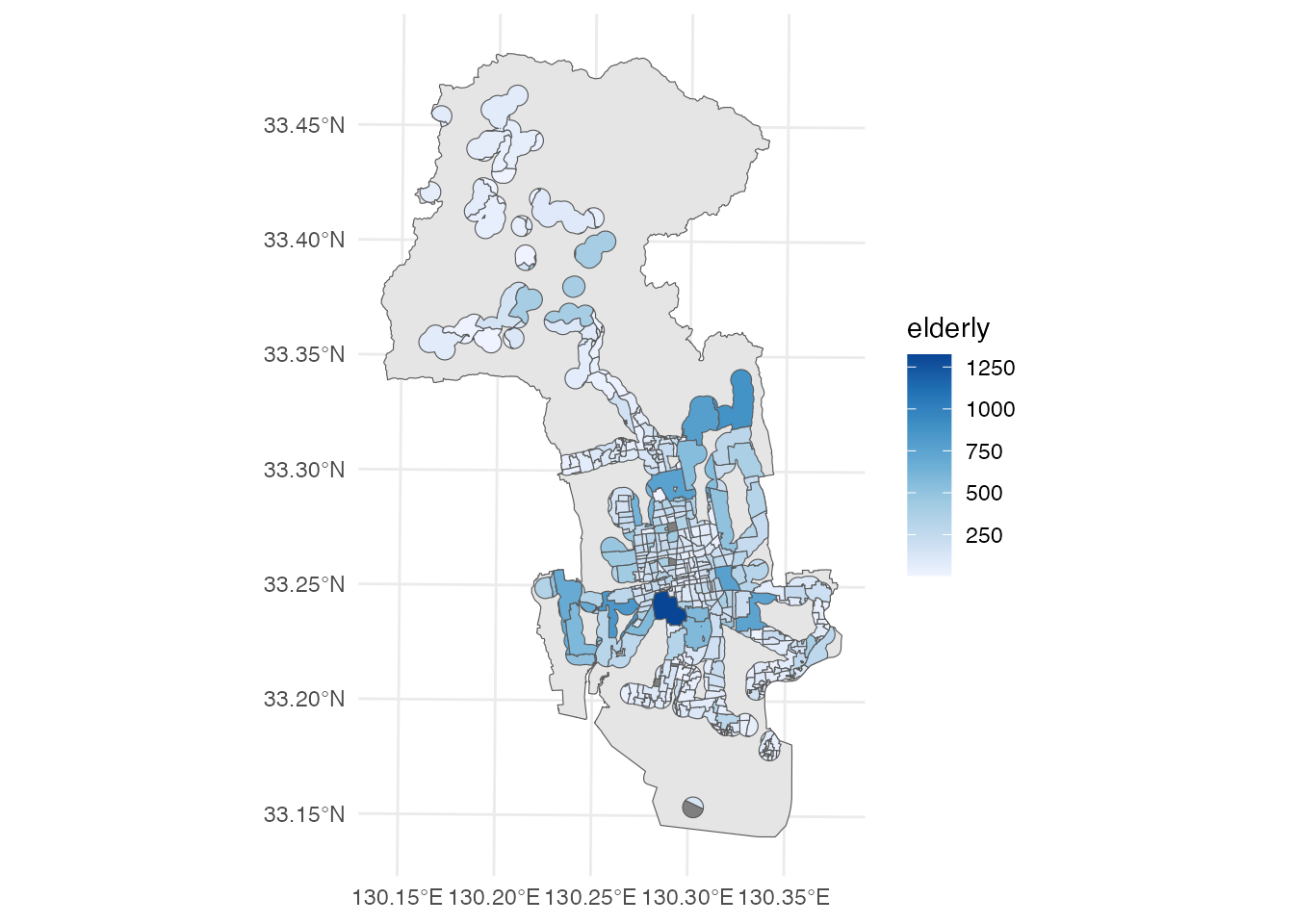

小地域領域のうちバッファーに含まれる部分が抽出できるので、この面積を計算することで小地域のなかのバッファー部分の面積比率が計算できることになります。小地域全体の高齢者人口にこの面積比率を掛けることで、小地域のうちバス停バッファー部分に相当する人口を推計します。つまり、面積按分によって対象地域の人口を推計しています。

# 面積按分による人口推計
intersect <- intersect |> 
  mutate(new_area = st_area(intersect),
         ratio = new_area / area,
         new_elderly = elderly * ratio)
head(intersect, 5)

Simple feature collection with 5 features and 37 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: -65669.76 ymin: 28615.66 xmax: -64125.32 ymax: 30085.38
Projected CRS: JGD2011 / Japan Plane Rectangular CS II
     KEY_CODE PREF CITY S_AREA PREF_NAME CITY_NAME         S_NAME KIGO_E HCODE
1 41201001001   41  201 001001    佐賀県    佐賀市 駅前中央一丁目   <NA>  8101
2 41201001002   41  201 001002    佐賀県    佐賀市 駅前中央二丁目   <NA>  8101
3 41201001003   41  201 001003    佐賀県    佐賀市 駅前中央三丁目   <NA>  8101
4 41201002001   41  201 002001    佐賀県    佐賀市     大財一丁目   <NA>  8101
5 41201002002   41  201 002002    佐賀県    佐賀市     大財二丁目   <NA>  8101
       AREA PERIMETER R2KAxx R2KAxx_ID KIHON1 DUMMY1 KIHON2  KEYCODE1  KEYCODE2
1 147281.68  1528.456      1         0   0010      -     01 201001001 201001001
2 108748.65  1371.930      2         1   0010      -     02 201001002 201001002
3 144423.54  1875.425      3         2   0010      -     03 201001003 201001003
4  74548.31  1150.161      4         3   0020      -     01 201002001 201002001
5 137859.16  1900.060      5         4   0020      -     02 201002002 201002002
  AREA_MAX_F KIGO_D N_KEN N_CITY KIGO_I KBSUM JINKO SETAI   X_CODE   Y_CODE
1          M   <NA>  <NA>   <NA>   <NA>    16   583   378 130.2978 33.26336
2          M   <NA>  <NA>   <NA>   <NA>    14  1081   576 130.2995 33.26637
3          M   <NA>  <NA>   <NA>   <NA>    19   832   432 130.3041 33.26694
4          M   <NA>  <NA>   <NA>   <NA>    11   337   202 130.3027 33.25728
5          M   <NA>  <NA>   <NA>   <NA>    10   797   413 130.3083 33.25828
   KCODE1 toddler elderly nursery1 nursery2            area
1 0010-01    15.4      73    FALSE    FALSE 147286.14 [m^2]
2 0010-02    61.2     132    FALSE    FALSE 108751.81 [m^2]
3 0010-03    51.8     144    FALSE    FALSE 144427.64 [m^2]
4 0020-01    12.8      93    FALSE    FALSE  74550.14 [m^2]
5 0020-02    35.6     200    FALSE    FALSE 137862.50 [m^2]
                        geometry        new_area         ratio  new_elderly
1 POLYGON ((-65198.19 29415.8... 147286.14 [m^2] 1.0000000 [1]  73.0000 [1]
2 POLYGON ((-65456.69 29590.8... 108751.81 [m^2] 1.0000000 [1] 132.0000 [1]
3 POLYGON ((-64843.62 29876.6... 144427.64 [m^2] 1.0000000 [1] 144.0000 [1]
4 POLYGON ((-64772.49 28755.2...  74550.14 [m^2] 1.0000000 [1]  93.0000 [1]
5 POLYGON ((-64354.59 28748.7... 135304.75 [m^2] 0.9814471 [1] 196.2894 [1]

面積按分によって求めた小地域の高齢人口を、全地域について足し上げることで集計しましょう。

# 集計
city_elderly <- district |> pull(elderly) |> sum(na.rm = TRUE) 
bus_elderly <- intersect |> pull(new_elderly) |> sum(na.rm = TRUE)
city_elderly

[1] 68281

bus_elderly

52375.62 [1]

bus_elderly / city_elderly * 100

76.706 [1]

佐賀市の高齢人口は68,281ですが、そのうちバス停から500 mの範囲の人口は52,376人と推計されました。高齢人口の約76.7％（およそ4分の3）はバスが利用しやすい場所に住んでいると言えそうです。

この数字は高いと思いますか、それとも低いと思いますか？

脚注

鄭美沙（2025）『「待機児童ゼロ」でも残る保育の課題～隠れ待機児童が招く就労意欲の低下～』（https://www.dlri.co.jp/report/ld/465501.html）↩︎
「他に利用可能な特定教育・保育施設又は特定地域型保育事業等があるにも関わらず、特定の保育所等を希望し、保護者の私的な理由により待機している場合には待機児童数には含めない」とされています。ここで「他に利用可能な特定教育・保育施設又は特定地域型保育事業等」とは、「開所時間が保護者の需要に応えている（例えば、希望の保育所と開所時間に差異がない）、立地条件が登園するのに無理がない（例えば、通常の交通手段により、自宅から20〜30分未満で登園が可能）」などとされています。↩︎
つまり、nursery |> group_by(P14_002) |> summarise(n = n())とほぼ同じ意味です。↩︎