# ライブラリのロード
library(tidyverse)
library(sf)
library(spatialEco)
library(mapview)
library(ggrepel)7: 人口重心
人口重心
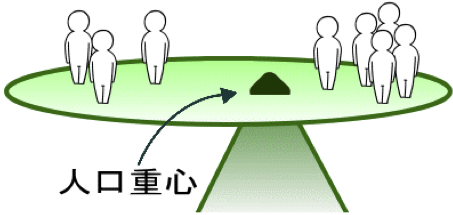
人口重心とは
人口重心とは、人口の一人一人が同じ重さを持つと仮定して、その地域内の人口が、全体として平衡を保つことのできる点のことをいいます。
日本では、国勢調査の人口分布をもとに計算されていて、日本の人口の地理的中心を表しているといえます。
人口重心の求め方
では、人口重心はどのように計算できるのでしょうか。 もし、地域に2人しかいないならば、その人口重心は2人の中点になることは明らかです。 では、地域に3人いる場合には、どうなるでしょうか?
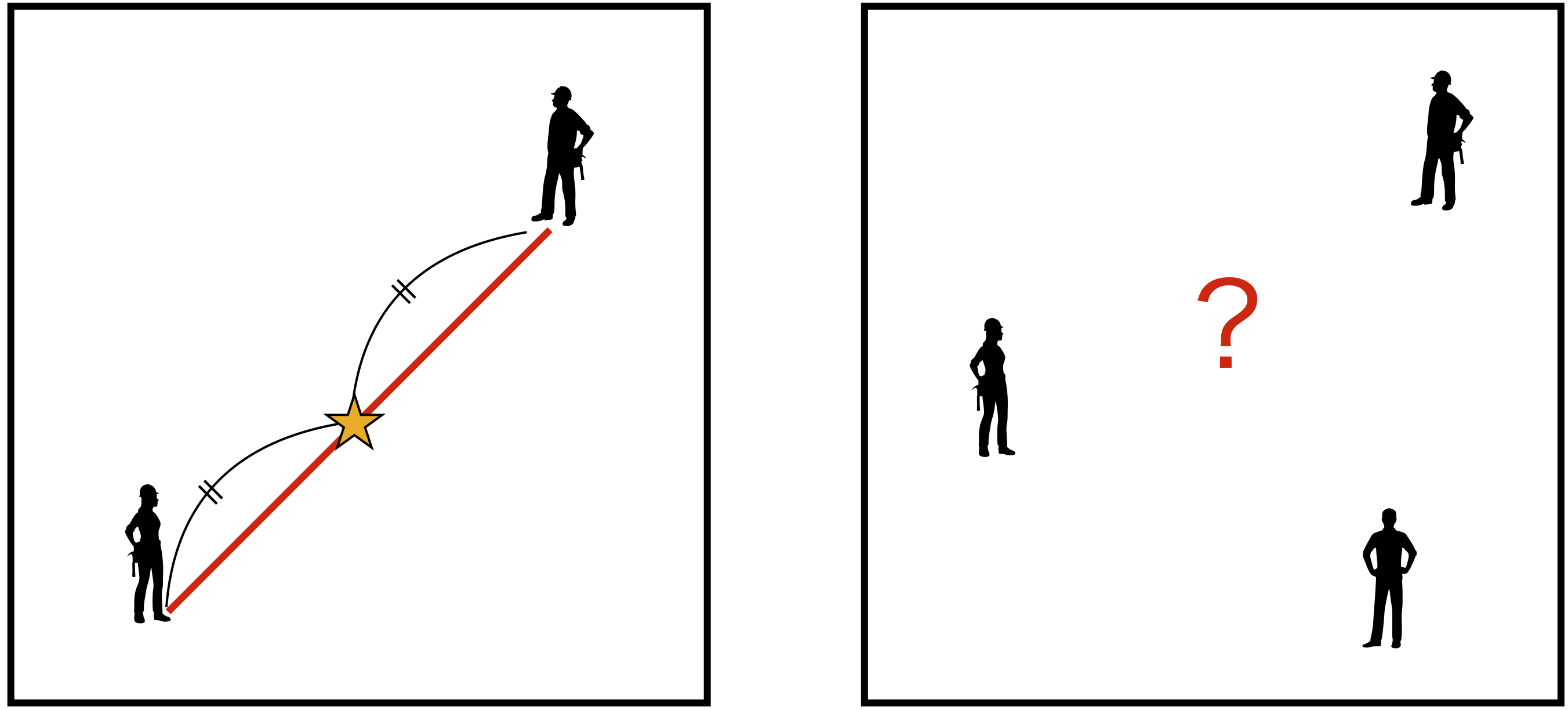
実は、3人の座標の縦軸と横軸それぞれの平均値を求めれば、それぞれが人口重心の縦軸と横軸の座標になります。 平面でバランスが取れるなら、2軸それぞれでバランスが取れるということです。
なぜ平均値で良いのか理解するために、下の図のように、重さが無視できる四角い板の上に何人かの人がいるような状況を考えます。
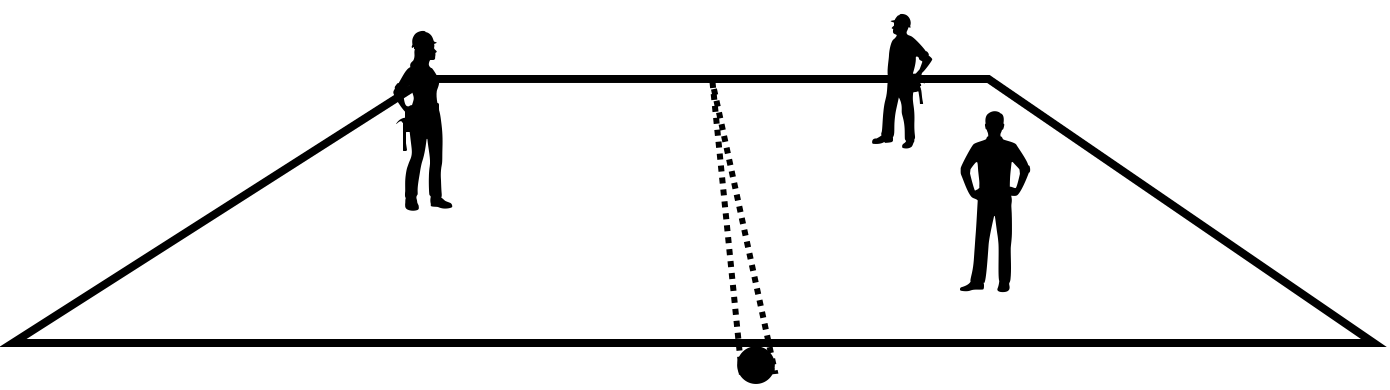
このとき、四角い板の下に、細長い丸棒を入れて、バランスが取れる棒の位置を探すことを考えます。 もう少し視点の位置を下げて、この状況を真横から見ると、下の図のように見えると思います。
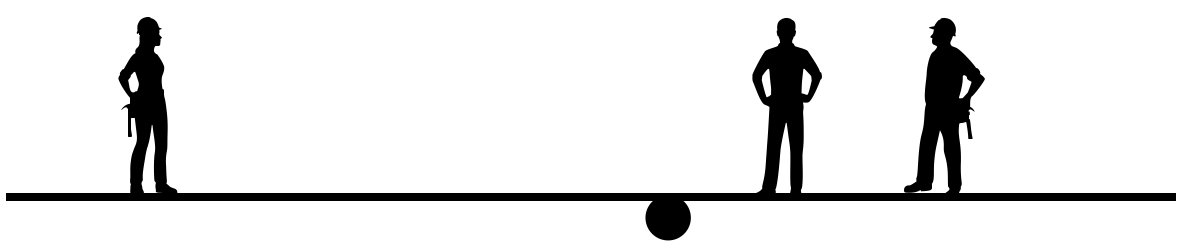
このシーソーのような状況において、バランスが取れる丸棒の位置はどのように求められるでしょうか。 丸棒の座標を\(x\)、各人の座標を\(x_i\)とするとき、バランスが取れているならば、
\[ \sum_{i=1}^N(x-x_i)=0 \]
が成り立ちます(てこの釣り合いの問題ですね)。 これを変形すると、
\[ x = \frac{1}{N}{\sum_{i=1}^Nx_i} \]
が得られますが、これは平均の定義そのものです。 したがって、各人の座標の平均値を計算し、その位置に丸棒を置けば、バランスが取れることがわかります。 丸棒の向きを(直交する方向に)変えてもう一度この作業を行えば、2つの丸棒の重なる地点が、全体として平衡を保つことのできる地点、すなわち人口重心だということになります。
以上から、人口重心の求め方を、数学的に表現すると以下のようになります。 個人\(i\)の座標を\((x_i, y_i)\)とするとき、 人口重心の\((\overline{x}, \overline{y})\)は \[ \begin{align} \overline{x}&=\frac{1}{N}\sum_{i=1}^Nx_i\\ \overline{y}&=\frac{1}{N}\sum_{i=1}^Ny_i \end{align} \] と表現できます。 \(\overline{x}\)と\(\overline{y}\)はぞれぞれ、\(x\)軸と\(y\)軸における 個人\(i\)の座標の平均値を意味しています。
また、データが地域ごとなどに集計されたデータから人口重心を計算することもできます。 この場合、地域\(i\)の座標を\((x_i, y_i)\)、地域\(i\)の人口を\(w_i\)、総人口を\(W\)とするとき、 人口重心の座標\((\overline{x}, \overline{y})\)は、 \[ \begin{align} \overline{x}&=\frac{\sum_iw_ix_i}{\sum_iw_i}=\frac{1}{W}\sum_iw_ix_i\\ \overline{y}&=\frac{\sum_iw_iy_i}{\sum_iw_i}=\frac{1}{W}\sum_iw_iy_i \end{align} \] と計算できます。 \(\overline{x}\)と\(\overline{y}\)はぞれぞれ、\(x\)座標と\(y\)座標における重み付き平均値を意味しています。
すなわち、人口重心は人口分布の平均値であることがわかります。
総務省統計局による人口重心の計算方法の説明では以下のように説明されています。 地域\(i\)の経緯度を\((\phi_i, \lambda_i)\)、地域\(i\)の人口を\(w_i\)とするとき、 人口重心の経緯度\((\overline{\phi}, \overline{\lambda})\)は、 \[ \begin{align} \overline{\phi}&=\frac{\sum_iw_i\phi_i\cos(\lambda)}{\sum_iw_i\cos(\lambda_i)}\\ \quad\overline{\lambda}&=\frac{\sum_iw_i\lambda_i}{\sum_iw_i} \end{align} \] で計算できます。
\(x\)座標、\(y\)座標ではなく、緯度経度から計算していることに注意してください。 高緯度ほど緯線の長さが短くなるので、\(\cos(\lambda)\)を掛けることでその影響を割り引いています。 これは、緯度経度に簡易的な投影変換を施していると考えることもできます。
人口重心の特徴
人口重心は以下の重要な性質を持っていいます。
- (個人の位置の)算術平均である
- (個人までの)距離の2乗の総和が最小となる地点である
- 「全体の重心」は「部分の重心」の重心である
このうち、1についてはすでに説明したので、2および3について解説します。
人口重心は距離の2乗和を最小にする
個人\(i\)の座標を\((x_i, y_i)\)とすると、地点\((x, y)\)までの距離の2乗の合計\(f(x,y)\)は \[ \begin{align} f(x,y)&=\sum_i\left(\sqrt{(x_i-x)^2+(y_i-y)^2}\right)^2\\ &=\sum_i(x_i-x)^2+\sum_i(y_i-y)^2 \end{align} \] となり、\(x\)座標に関する偏差平方和と\(y\)座標に関する偏差平方和の合計であることがわかります。
偏差平方和を最小にするのは平均値ですから、\(f(x,y)\)を最小にする\(x,y\)はそれぞれ、\(x_i\)と\(y_i\)の平均値であることがわかります。
「偏差平方和を最小にするのが平均値」であることは、以下のように確認できます(平方完成すればよい)。 \[ \begin{align} g(x) &= \sum_i(x_i-x)^2 \\ &= \sum_i(x_i^2 - 2x_ix + x^2) \\ &= Nx^2 - \left(2\sum_ix_i\right)x + \sum_ix_i^2 \\ &= N\left\{x^2 - \left(\frac{2}{N}\sum_ix_i\right)x\right\} + \sum_ix_i^2 \\ &= N(x^2 - 2\overline{x}) + \sum_ix_i^2 \\ &= N(x - \overline{x})^2 - N\overline{x}^2 + \sum_ix_i^2 \end{align} \] \(g(x)\)が最小になるのは、\(x = \overline{x}\)すなわち\(x\)が平均値のときです。
\(x_i\)と\(y_i\)の平均値を座標にもつ点は人口重心に他なりませんから、 これで「人口重心は各個人までの距離の2乗和を最小にする地点である」ということが確認できました。
これに関連して、距離の2乗の重み付きの合計の等高線図を描くと、人口重心を中心とする同心円になるという性質があります。 距離の2乗和を最小にする地点が人口重心なのですから、人口重心から離れると距離の2乗和が増加することは明らかです。 この時、距離の距離の2乗和の等高線図を書くと、人口重心を中心とする同心円になることが知られています。 これは、\(f(x,y)\)の式が人口重心を中心とする円の方程式になることから明らかです。
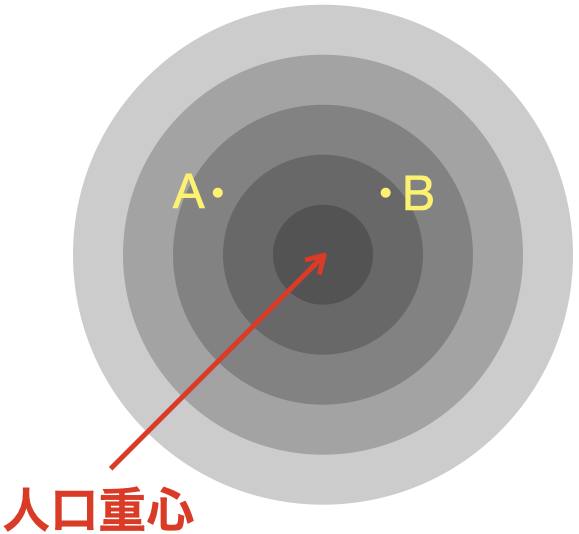
このことから、 全人口までの距離の2乗の重み付きの和は、人口重心からの距離が近いほど小さくなる、といえます。
\[ \sum_i(x_i-x)^2+\sum_i(y_i-y)^2=F \] となる地点\((x, y)\)の軌跡を考えます。先ほどの式展開から、 \[ \begin{align} \sum_i(x_i - x)^2 + \sum_i(y_i - y)^2 &= F \\ N(x - \overline{x})^2 - N\overline{x}^2 + \sum_ix_i^2 + N(y - \overline{y})^2 - N\overline{y}^2 + \sum_iy_i^2 &= F\\ (x - \overline{x})^2 + (y - \overline{y})^2 &= \frac{F - \sum_i(x_i^2 - y_i^2)}{N} + \overline{x}^2 + \overline{y}^2\\ (x - \overline{x})^2 + (y - \overline{y})^2 &=C^2 \end{align} \] となりますが、これは中心が\((\overline{x}, \overline{y})\)、すなわち人口重心である円の軌跡に他なりません。
これは割と面白い性質で、公共施設の立地の評価指標として人口重心からの直線距離が使われることがあるのですが、各市民からの近さを直線距離の2乗で評価するような場合においては(遠方の人の影響を近くに人よりも大きく評価するような場合)、これは理論的に全く正しいということになります。 そのような状況においては、図の地点Aと地点Bを比べると、人口重心に近いBの方が施設立地点として望ましいということになります。
全系の重心は部分系の重心の重心である
人口重心は人口分布の平均値だ、ということを思い出してください。
全体の平均値は、部分の平均値の平均値であることは、疑う余地がないと思います(もちろんきちんと重み付き平均値を計算するとして)。 人口分布の平均値である人口重心の計算でもそれは同じです。
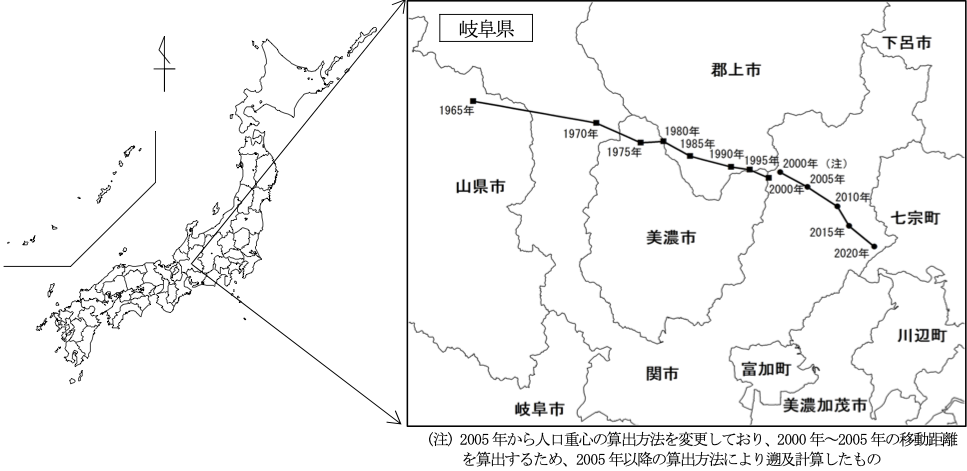
実際、日本の人口重心の計算では、まず市区町村の人口重心を計算し、これに市区町村の人口の重みをかけた都道府県の人口重心を計算します。 さらに都道府県の人口重心に都道府県人口の重みをかけた人口重心を計算し、これを日本の人口重心としています。
人口重心の軌跡
人口重心は、その位置そのものよりも、その変化(移動)や差を観察することに、より重要な意味があります。 これは、例えば、ある都市のある指標(市内の平均値)について考えた時に、その指標そのものよりも、 それが過去と比べてどのように変化したや、あるいは他の都市と比べてどのような差があるかをみるためにとても有用であることと同じです。
人口学者の大友篤は、
人口重心の位置の時系列変動を把握することによって、人口分布の時系列的推移を端的に知ることができるという点で、人口の地域分布の有用な測度である。
と述べています(大友、2002)。
総務省統計局は、国勢調査から日本の人口重心を計算し、その時系列変化を合わせて公表しています。 その資料の中で、
我が国の人口重心の動きを長期的にみると、首都圏への人口の転入超過が続いてきたことなどにより、おおむね東南東方向へ移動しています。
と公表しています。 日本の人口重心の軌跡が、日本の社会経済の動向を反映していると考えられます。
演習
準備
以下の作業を行ってください。
- プロジェクトを作成する。
- 作成したプロジェクトフォルダの中に、“data”フォルダを作成する。
- スクリプトファイルを作成する。
spatialEcoパッケージをインストールする。
今回の演習では、spatialEcoというパッケージを新たに使用しますので、インストールしてください。
今回の演習で利用するパッケージは以下の6つです。 以下のコードをスクリプトフィルに入力し、実行してください。
演習1 佐賀市の人口重心を計算する
佐賀市の2020年の人口重心を計算し、地図に表示してみましょう。
データダウンロード
人口データは、2020年国勢調査の基本単位区データを使います。 e-Statからダウンロードすることが可能です。
ブラウザでe-Statのページを開いたら、「地図」→「境界データダウンロード」の順に進みます。
データダウンロードのページに進んだと思いますので、「小地域」→「国勢調査」→「2020年」→「小地域(基本単位区)(JGD2011)」の順にクリックしてください。
データ形式は、今回は「世界測地系平面直角座標・Shapefile」を選んでください。
地域は「41 佐賀県」を選択します。 「41201 佐賀市」の右にある[世界測地系平面直角座標・Shapefile]のボタンをクリックすると、zip圧縮されたファイル(B002005212020XYSWC41201-JGD2011.zip)がダウンロードされます。
ダウンロードされたzipファイルを右クリックして解凍したら、解凍したフォルダ(B002005212020XYSWC41201-JGD2011) をプロジェクトのdataフォルダに移動しましょう。
人口重心の計算
まずは、データをst_read関数を使って読み込みます。
# 基本単位区データの読み込み
basic_unit <- st_read("data/B002005212020XYSWC41201-JGD2011/r2kb41201.shp")Reading layer `r2kb41201' from data source
`/Users/kzktmr/Documents/LectureNotes/EconomicGeography/data/B002005212020XYSWC41201-JGD2011/r2kb41201.shp'
using driver `ESRI Shapefile'
Simple feature collection with 3835 features and 37 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -80084.88 ymin: 15840.25 xmax: -57844.26 ymax: 53682.39
Projected CRS: JGD2011 / Japan Plane Rectangular CS IIこれは、国勢調査基本単位区のポリゴンデータです。 基本単位区は、小地域よりも細かな地域区分です。小地域が住所表示(○丁目○番○号)の「丁目」に対応しているのに対し、 基本単位区は「番」に対応していて、1つの単位区はおよそ数十世帯の規模であるといわれています。
人口重心を計算するために、基本単位区の代表点を求める必要があります。 これには、第4回の講義で紹介したsf::st_centroid関数を使いましょう。 これで、基本単位区ポリンゴンデータを、ポイントデータに変換できます。
ポイントデータから人口重心を計算するには、今回はspatialEcoパッケージのwt.centroid関数を使います。 引数には、ポイントデータと、データのうち人口データとして使う列名を文字列で与えます。 これらの処理をパイプ演算子で繋ぐと次のようになります。
# 佐賀市の人口重心を計算する
centroid <- basic_unit |> st_centroid() |> wt.centroid(p = "JINKO")Warning: st_centroid assumes attributes are constant over geometries人口重心を佐賀市の基本単位区の地図に重ねて表示してみましょう。
# 佐賀市の人口重心を地図に表示する
ggplot() +
geom_sf(data = basic_unit) +
geom_sf(data = centroid, color = "red") +
theme_minimal()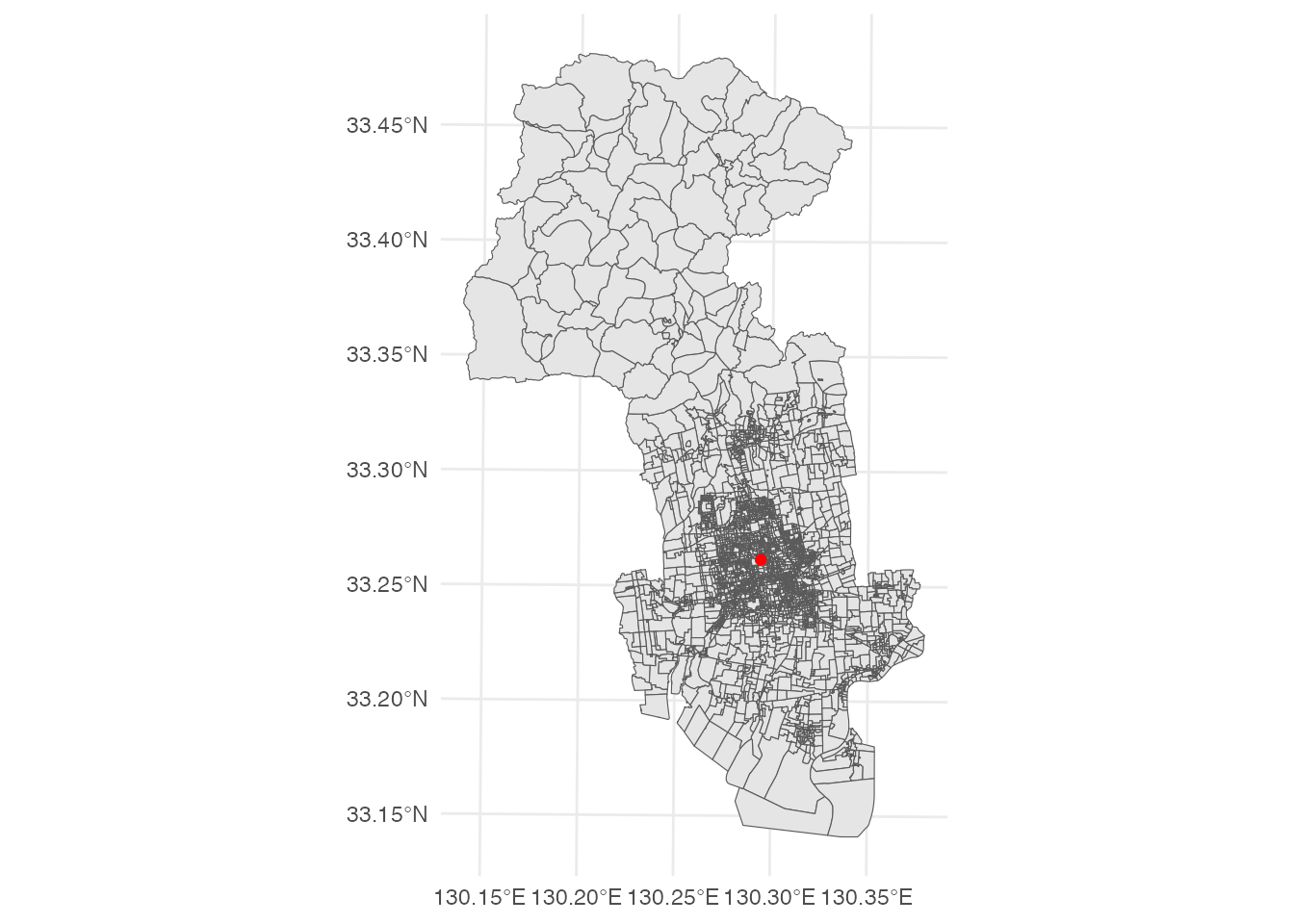
この人口重心の緯度経度を確認しておくと、その座標は(130.2942, 33.26155)です。
# 佐賀市の人口重心の経緯度
st_transform(centroid, 6668) |> st_coordinates() X Y
[1,] 130.2942 33.26155国勢調査に基づいた市町村の人口重心を総務省統計局が公表しています。 これによると、佐賀市の人口重心の座標は(130.294233, 33.261548)とのことですから、 なかなか近い位置になったのではないでしょうか。
佐賀市の2020年の人口重心は、佐賀市神野東1丁目(JR佐賀駅の南西約500 m)に位置するようです。
人口重心を中心とする同心円を重ねてみましょう。 ここでは、半径を1,000〜5,000 mまで、1,000 m刻みで5つの円を描いています。 同心円はst_buffer関数で作成しています。
# 人口重心を中心とする同心円を描く
cc <- seq(1000, 5000, 1000) |>
map(function(x){st_buffer(centroid, dist = x)}) |>
bind_rows()
ggplot() +
geom_sf(data = basic_unit) +
geom_sf(data = centroid, color = "red") +
geom_sf(data = cc, color = "red", fill = NA) +
theme_minimal()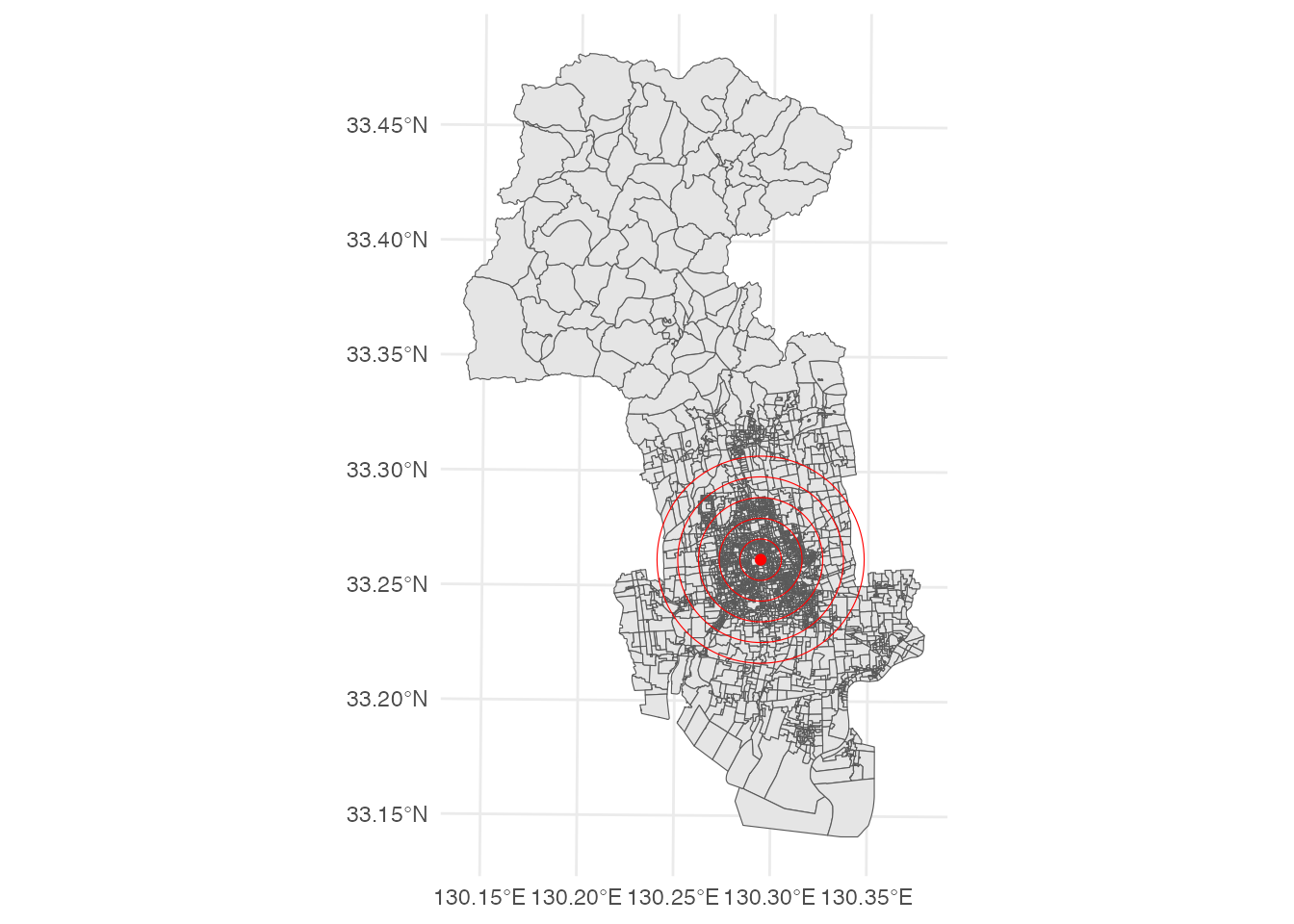
mapviewでも見てみましょう。
# 人口重心を中心とする同心円を描く(mapview版)
mapview(centroid, col.regions = "red") +
mapview(cc, color = "red", alpha.region = 0)purrr::map関数
map関数はpurrrパッケージ(tidyverseに含まれる)の関数で、これを使うと、ループ処理をスマートに書くことができます。 例えば、下の例のように、1〜10の数字に関数fを適用する場合には、forループを使っても良いですが、パイプ演算子とmap関数を使って書くこともできます。map関数の結果はリスト構造になっていますので、パイプ演算子を使って、そのまま次の処理に渡すこともできます。
f <- function(x){x^2}
# forループの場合
y1 <- list(NULL)
for(x in 1:10){
y1[[x]] <- f(x)
}
y1
# map関数の場合
y2 <- 1:10 |> map(f)
y2先の例では、1000、2000、3000、4000、5000という数字のベクトルを、wt.centroid関数のdist引数に順番に順番に渡して、5つの円をリストで受け取っています。 そしてさらに、それをbind_row関数でデータフレームに変換しています。
演習2 佐賀県の人口重心の推移を見る
データのダウンロード
人口データは、2000年から2020年までの国勢調査の小地域データを使います。 e-Statからダウンロードすることが可能です。
ブラウザでe-Statのページを開いたら、「地図」→「境界データダウンロード」の順に進みます。
データダウンロードのページに進んだと思いますので、「小地域」→「国勢調査」の順にクリックしてください。
2000年から2020年までの5回の国勢調査のデータをそれぞれダウンロードしてください。 使用するデータですが、いずれの年次においても利用可能な「小地域(町丁・字等)(JGD2000)」に統一します。
また、データ形式は、今回も「世界測地系平面直角座標・Shapefile」を選んでください。
地域は「41 佐賀県」を選択します。 「41000 佐賀県全域」の右にある[世界測地系平面直角座標・Shapefile]のボタンをクリックすると、zip圧縮されたファイルがダウンロードされます。
ダウンロードされたzipファイルを右クリックして解凍したら、解凍したフォルダ をプロジェクトのdataフォルダに移動しましょう。
2000年から2020年まで、この操作を5回繰り返してください。
人口重心の計算
人口重心の計算は、演習1と同様に、sf::st_centroid関数とspatialEco::wt.centroid関数を使います。 はじめにlist.files関数を使って、dataフォルダ以下にあるファイルのうち、名前が”ka41.shp”で終わるものを列挙しています(つまり今ダウンロードした佐賀県のデータ)。 このファイルに対して、purrr::map関数を使って、順番に、sf::st_read関数で読み込み、st_centroid関数でポイントデータに変換し、wt.centroid関数でJINKOをウェイトにした重心を求めています。 dplyr::bind_rows関数で1つのsfファイルに結合したあと、 dplyr::mutate関数で、データのyear列に調査年の情報を付加しています。
# 5つのファイルのリスト
shp_files <-
list.files('data', full.names = TRUE, recursive = TRUE, 'ka41.shp$')
# 5つのファイルを読み込み、それぞれの重心を計算
centroids <-
shp_files |>
map(function(f){st_read(f, quiet = TRUE) |> st_centroid() |> wt.centroid(p = "JINKO")}) |>
bind_rows() |> mutate(year = as.factor(seq(2000, 2020, 5)))Warning: st_centroid assumes attributes are constant over geometries
Warning: st_centroid assumes attributes are constant over geometries
Warning: st_centroid assumes attributes are constant over geometries
Warning: st_centroid assumes attributes are constant over geometries
Warning: st_centroid assumes attributes are constant over geometriesmapview関数を使って、地図に表示してみましょう。 ここでは調査年で色をつけています。
# 佐賀県の人口重心の推移
mapview(centroids, zcol = 'year')佐賀県の人口重心は、この20年間ずっと小城市に存在することがわかります。 しかし細かく見ると、2000年(小城市小城町栗原)から2020年(小城市小城町畑田)にかけて、 ずっと東北東に移動していることがわかります。 さらにその移動速度は加速しているように見えます。 近年の鳥栖市の人口増加を反映した結果ではないかと思います(2015年から2020年にかけて人口が増加した佐賀県の市町は鳥栖市・みやき町・上峰町の3市町のみ)。
演習3 佐賀県の年齢別人口重心を計算する
データのダウンロード
境界データは、演習2で利用した2020年の佐賀県小地域データを使いましょう。 新たに、5歳階級年齢別人口データを取得して、境界データに結合することにします。 データはe-Statからダウンロードすることが可能です。
ブラウザでe-Statのページを開いたら、「地図」→「統計データダウンロード」の順に進みます。
データダウンロードのページに進んだと思いますので、「国勢調査」をクリックしてください。
「2020年」→「小地域(町丁・字等)」をクリックすると、利用可能なデータのリストが表示されますので、「年齢(5歳階級、4区分)別、男女別人口」をクリックしてください。
地域は「41 佐賀県」を選択します。 「41佐賀県」の右にある[CSV]のボタンをクリックすると、zip圧縮されたファイルがダウンロードされます。
また、右上にある紫色の[定義書]ボタンをクリックして、データの定義書を入手しておきましょう。
ダウンロードされたzipファイルを右クリックしてすべて展開したら、展開したフォルダと定義書のPDFファイルを、プロジェクトのdataフォルダに移動しましょう。
年齢階級別人口データの読み込みと結合
ファイルの拡張子は[.txt]になっていますが、中身はカンマ区切り(つまりCSV)になっていますので、 read_csv関数で読むことができます。 しかし、ちょっとクセのある1ファイルのなので、Rで読み込むためには少し工夫が必要です。
まず、データの2行(列名と項目名)だけを、全て文字列として読み込みます。 読み込むと2行×67列のデータフレームになりますが、の行列を入れ替えて(as.matrix関数で行列に変換、t関数で転置)、改めてデータフレーム(ティブル)に変換し、列名をcolとjpにしています。
# 統計データのヘッダ情報だけを読む
header <-
read_csv("data/tblT001082C41.txt", col_types = "c",
col_names = FALSE, n_max = 2,
locale = locale(encoding = "cp932")) |>
as.matrix() |> t() |> as_tibble(.name_repair = "minimal") |>
set_names(c('code', 'name'))
glimpse(header)Rows: 67
Columns: 2
$ code <chr> "KEY_CODE", "HYOSYO", "CITYNAME", "NAME", "HTKSYORI", "HTKSAKI", …
$ name <chr> NA, NA, NA, NA, NA, NA, NA, "総数、年齢「不詳」含む", "総数0〜4歳", "総数5〜9歳", "総…もう一度read_csvファイルで読み込みます。今度は先頭の2行を読み飛ばし、列名には先ほど読み込んだheader$colを使います。 データが利用できない「」(空白)、「-」(皆無又は定義上該当数値がないもの)、「X」(数値が秘匿されているもの)は欠損値(NA)とします。
境界データの結合する時のキーとなるKEY_CODEは、文字列に変換しています(データの型が一致していないと、キーとして使えないので)。 また、人口がNAのままだと人口重心を計算できないので、全ての数値データ(人口データ)について、replace_na関数を使ってNAを0で置き換えておきます。
# 統計データ本体を読む
data_2020 <-
read_csv("data/tblT001082C41.txt",
col_names = pull(header, code),
na = c("", "-", "X"), skip = 2,
locale = locale(encoding = "cp932")) |>
mutate(KEY_CODE = as.character(KEY_CODE),
across(where(is.numeric), ~replace_na(.x, 0)))Rows: 2567 Columns: 67
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (4): CITYNAME, NAME, HTKSAKI, GASSAN
dbl (63): KEY_CODE, HYOSYO, HTKSYORI, T001082001, T001082002, T001082003, T0...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.head(data_2020)# A tibble: 6 × 67
KEY_CODE HYOSYO CITYNAME NAME HTKSYORI HTKSAKI GASSAN T001082001 T001082002
<chr> <dbl> <chr> <chr> <dbl> <chr> <chr> <dbl> <dbl>
1 41201 1 佐賀市 <NA> 0 <NA> <NA> 233301 9001
2 412010010 3 佐賀市 駅前中央… 0 <NA> <NA> 2496 110
3 412010010… 4 佐賀市 駅前中央… 0 <NA> <NA> 583 12
4 412010010… 4 佐賀市 駅前中央… 0 <NA> <NA> 1081 53
5 412010010… 4 佐賀市 駅前中央… 0 <NA> <NA> 832 45
6 412010020 3 佐賀市 大財 0 <NA> <NA> 4037 145
# ℹ 58 more variables: T001082003 <dbl>, T001082004 <dbl>, T001082005 <dbl>,
# T001082006 <dbl>, T001082007 <dbl>, T001082008 <dbl>, T001082009 <dbl>,
# T001082010 <dbl>, T001082011 <dbl>, T001082012 <dbl>, T001082013 <dbl>,
# T001082014 <dbl>, T001082015 <dbl>, T001082016 <dbl>, T001082017 <dbl>,
# T001082018 <dbl>, T001082019 <dbl>, T001082020 <dbl>, T001082021 <dbl>,
# T001082022 <dbl>, T001082023 <dbl>, T001082024 <dbl>, T001082025 <dbl>,
# T001082026 <dbl>, T001082027 <dbl>, T001082028 <dbl>, T001082029 <dbl>, …小地域ポリゴンデータを読み込み、小地域ポリンゴンの代表点をst_centroid関数求めます。 これに、先ほど読み込んだデータファイルをKEY_CODEをキーにしてleft_join関数で結合します。
# 地図データに統計データを結合する
saga_2020 <-
st_read("data/A002005212020XYSWC41/r2ka41.shp") |>
group_by(KEY_CODE) |> summarise() |>
st_centroid() |>
left_join(data_2020, by = join_by(KEY_CODE)) Reading layer `r2ka41' from data source
`/Users/kzktmr/Documents/LectureNotes/EconomicGeography/data/A002005212020XYSWC41/r2ka41.shp'
using driver `ESRI Shapefile'
Simple feature collection with 2300 features and 29 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: -117268.6 ymin: -5213.548 xmax: -42584.04 ymax: 69215.29
Projected CRS: JGD2000 / Japan Plane Rectangular CS IIWarning: st_centroid assumes attributes are constant over geometries5歳階級ごとの人口重心を計算します。wt.centroid関数に与える引数に、 それぞれの人口階級に対応する列名を文字列で与えます。 ここでは、先ほど作成したheaderデータフレームから、項目名称が「総数」から始まるものだけを取り出し(str_detect関数はstringrパッケージの関数で、“文字列”が”パターン”を含むかどうかをTRUEまたはFALSEで返します)、ageというデータフレームを作成しています。 ageの内容を確認すると、“総数、年齢「不詳」含む”から”総数75歳以上”まで、20の列名が抽出されていることがわかります。
ageに含まれる列名を、map関数によって次々にwt.centroid関数のp引数に渡し、人口重心を計算します。 結果はリストで返されるので、これをbind_rows関数で1つのポイントデータにまとめています。
# 人口重心を計算する年齢階級のリスト
age <- header |>
filter(str_detect(name, '^総数')) |>
mutate(
name = str_remove(name, '^総数'),
name = if_else(name == "、年齢「不詳」含む", "総数", name),
name = zipangu::str_conv_zenhan(name, to = "hankaku"),
name = factor(name, levels = name))
age# A tibble: 20 × 2
code name
<chr> <fct>
1 T001082001 総数
2 T001082002 0〜4歳
3 T001082003 5〜9歳
4 T001082004 10〜14歳
5 T001082005 15〜19歳
6 T001082006 20〜24歳
7 T001082007 25〜29歳
8 T001082008 30〜34歳
9 T001082009 35〜39歳
10 T001082010 40〜44歳
11 T001082011 45〜49歳
12 T001082012 50〜54歳
13 T001082013 55〜59歳
14 T001082014 60〜64歳
15 T001082015 65〜69歳
16 T001082016 70〜74歳
17 T001082017 15歳未満
18 T001082018 15〜64歳
19 T001082019 65歳以上
20 T001082020 75歳以上# 年齢階級ごとの人口重心を計算
by_age <-
age |> pull(code) |>
map(function(x){wt.centroid(saga_2020, p = x)}) |>
bind_rows() |> mutate(age = age |> pull(name))
by_ageSimple feature collection with 20 features and 2 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: -76726.81 ymin: 31844.52 xmax: -72655.47 ymax: 32840.51
Projected CRS: JGD2000 / Japan Plane Rectangular CS II
First 10 features:
ID geometry age
1 1 POINT (-75083.54 32315.1) 総数
2 1 POINT (-74303.65 32583.87) 0〜4歳
3 1 POINT (-74860.14 32531.79) 5〜9歳
4 1 POINT (-75038.69 32763.68) 10〜14歳
5 1 POINT (-74423.53 32840.51) 15〜19歳
6 1 POINT (-72655.47 32477.62) 20〜24歳
7 1 POINT (-73859.32 32455.95) 25〜29歳
8 1 POINT (-74073.46 32562.21) 30〜34歳
9 1 POINT (-74466.68 32458.25) 35〜39歳
10 1 POINT (-74291.16 32662.23) 40〜44歳最後に、結果を地図で確認します。
ggplot() +
geom_sf(aes(color = age), data = by_age) +
ggrepel::geom_text_repel(
aes(label = age, geometry = geometry),
stat = "sf_coordinates",
data = by_age
) +
theme(axis.title = element_blank(), legend.position = "none")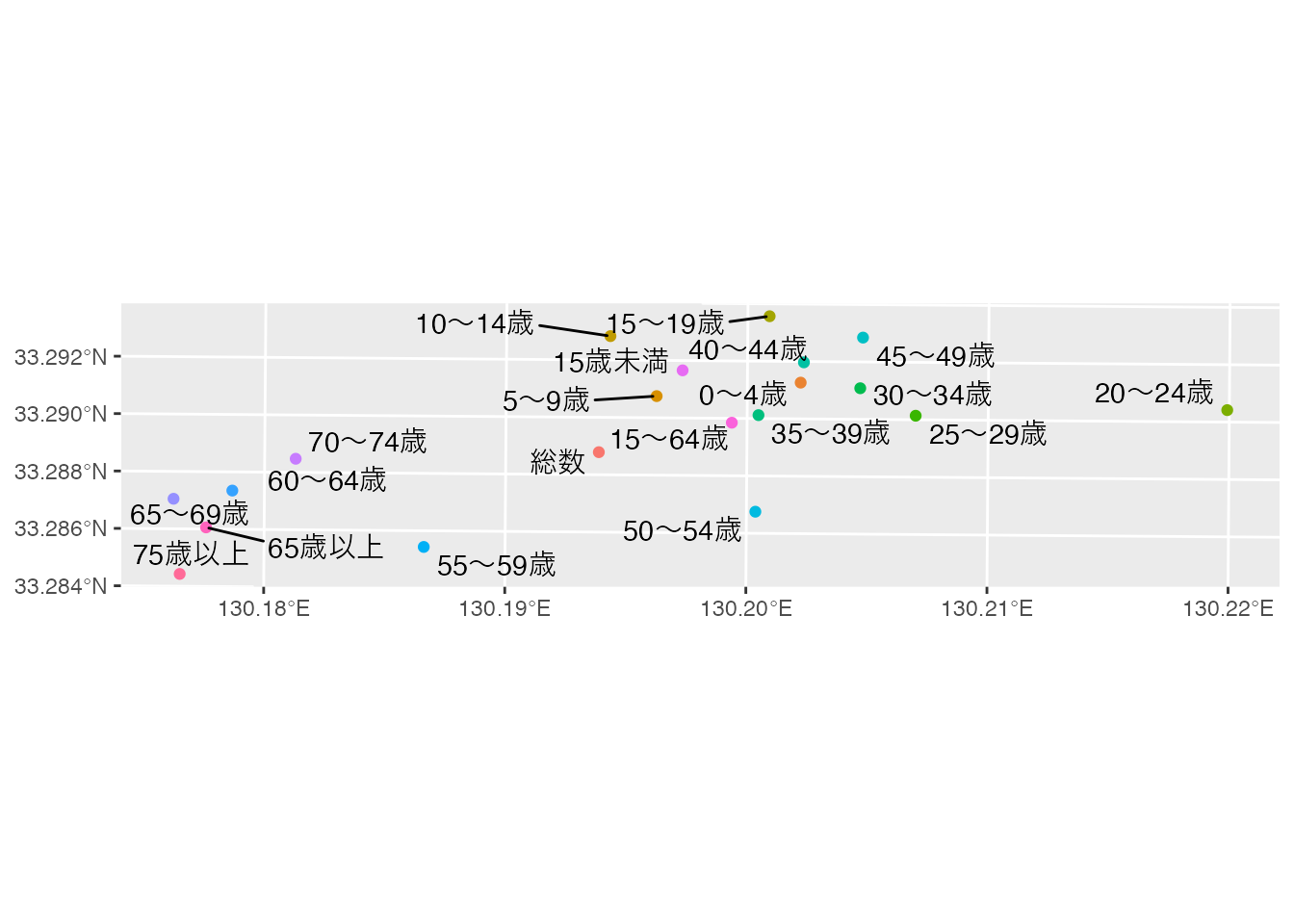
これを見ると、年齢階級別人口重心は、東西方向に広がって分布していることがわかります。 年齢階級別に見ると、もっとも東にあるのが20〜24歳、もっとも西にあるのが65〜69歳です。 全体的には、若い人たちほど東寄りに住んでいて、高齢の人ほど西寄りに住んでいます。 しかし、0〜4歳あるいは5〜9歳の人口重心は、それぞれ30〜34歳、35〜39歳の人口重心の近くに位置していて、 それらの世代が同じ世帯に属して(同居して)いることを想像させます。
このように、世代などのグループごとの人口重心(居住地の地理的な平均)を計算することで、グループによる居住地の分布の特徴を端的に、かつ視覚的に把握することが可能になります。
ちなみに、このような同じ時期に生まれた集団のことをコーホートと呼びます。 2020年における20〜24歳コーホートは、2015年調査における15〜19歳コーホートに相当します。 複数の調査年のデータを使って、コーホートごとの人口重心の移動傾向を調べることも、興味深いのではないかと思います。
脚注
1行目に列名(英数字)が、2行目に日本語の項目名称が記載されています。↩︎
