1: イントロダクション

公開

2024年4月10日

更新日

2024年7月31日

地理情報をコンピュータで扱うことの意義

都市や地域を対象とした経済分析および政策分析においては、近年、地理的位置や距離にもとづいた分析が不可欠になっています。その背景としては、政策の決定過程において、エビデンスに基づいた政策立案（EBPM：Evidence Based Policy Making）が求められるようになってきたととも関係しますが、近年、さまざまな地理空間データの整備が進み利用可能になったことが挙げられます。

そこで、この講義では、

地理情報を扱うための基礎知識を習得すること
地理情報を可視化する手法を学ぶこと
地域の経済分析に応用するための手法を学ぶこと

を目標にしたいと思います。

地図とは何か

地理情報をコンピュータで扱うことの話をする前に、地図とは何か、考えてみましょう。辞書の定義によると、

地球表面の一部または全部の状態を，一定の割合で縮め，文字・記号を用いて平面上に表したもの。

とあります（スーパー大辞林）。

私たちが目にする地図製品には、どのようなものがあるでしょうか。紙の地図としては、住宅地図や道路地図、都市地図などは、書店でも販売されている身近な地図の一つです。国土地理院が発行している地形図はを見たことがある人もいるでしょう。登山などをする人にはお馴染みの地図です。

これらの地図はいずれも、一定の縮尺によって現実世界をミニチュア化し、持ち運びに便利な紙や冊子の上に表したものです。また、道路や建物を外形のみで表現するなど現実世界をデフォルメし、地図記号などを使いながら、限られた紙面に必要な情報を効率的に配置しています。

この地図によって、私たちは、一定範囲の地域を概観あるいは俯瞰できるようになります。ドライブをするときには、道路地図を見ながら最寄りのコンビニやガソリンスタンドを探すことが可能になりました。あるいは、商品を配達するドライバーは、住宅地図によって目的の住宅の場所を探すことができるようになりました。

地図のデジタル化

近年、紙の地図がコンピュータ上に表現されたデジタル地図が利用されるようになりました。カーナビ（カー・ナビゲーション・システム）が普及し、紙の道路地図はほとんど使われなくなりました。カーナビの発展・普及には、現在位置のデジタル座標を取得できるGPS（Global Positioning System）の民間開放も大きく貢献しました。

カーナビと道路地図の最も大きな違いの1つは、地理情報の検索ができるかどうかでしょう。検索はコンピュータが最も得意とする分野の1つで、カーナビによって、目的地までの最適な経路が簡単に検索できるようになりました。また、近隣の店舗の検索も簡単になりました。最近ではスマートフォンやタブレットなどでもデジタル地図が利用可能になり、いつでもどこでも、地図の検索が可能なりました。

さらに、デジタル地図を用いることで、距離や面積の計測も容易になりました。さらに、 統計データの可視化や地理的集計なども、以前と比べると手軽で身近なものになりました。

地理情報システム

そのような、地理的な情報をコンピュータで扱うための仕組みを、GIS（Geographic Information System：地理情報システム）と呼びます。私たちが日常的に使っているGoogleマップに代表されるデジタル地図は、はGISの1つであると言えます。なので、Googleマップを使いこなしている人は、すでにGISを使いこなしている、と言えるのです。

もちろん、さらに高度な分析を行うための専用ソフトウェアもあります。そのような専用ソフトウェアを使うことで、デジタル地図だけではできないような計測、可視化、分析が可能になります。有名なGISソフトウェアとしては、商用ソフトのArcGISやフリーソフトのQGISがあります。しかし、この講義ではそのような専用ソフトを利用せず、統計解析ソフトであるRとその統合開発環境であるRStudioを使います。

これらのソフトを利用することにした理由としては、

フリーウェアであること
経済分析との親和性が高いこと
分析の再現可能性が高いこと

などを挙げることができます。しかしいずれにしても、大切なことは、どのソフトを使うかではなく、地理情報をどう扱うかを知っていることです。その知識さえ身についていれば、皆さんはどのようなソフトウェアでも使いこなすことができるはずです。

測地参照系（CRS）について

もう一度、先ほどの辞書にある地図の定義を見てみましょう。

地球表面の一部または全部の状態を，一定の割合で縮め，文字・記号を用いて平面上に表したもの。

つまり、地図表現では、地球表面という球面（3次元）の情報を平面（2次元）に変換する必要があります。言い換えると、地理座標系（緯度・経度・高度）を投影座標系（平面のXY座標）に変換する必要があるということです。皆さんも、これまでに地図投影法について教わったことがあると思います。メルカトル図法、ミラー図法、モルワイデ図法、正距方位図法など、投影法の名前を聞いたことがあるのではないでしょうか。面積・距離・角度・形状を同時に正確に表現できない、などということを覚えている人もいるかもしれません。

私たちの先人は、丸い地球を紙の地図に表現するために、さまざまな工夫をしてきました。地理情報を扱うにあたって、どうしても避けては通れない測地参照系（CRS：Coordinate Reference System）の話をしておきたいと思います。

地理座標系

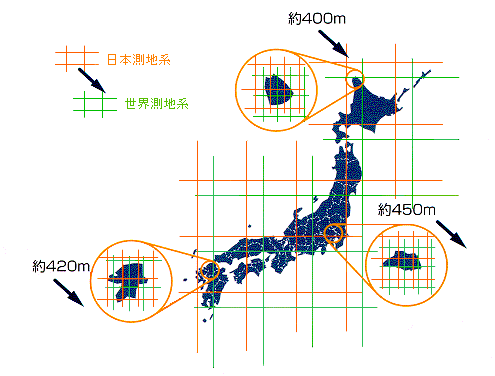
地理座標系というのは、3次元である地球上の位置を、緯度と経度で表現する座標系です。経度は、その地点と北極・南極を通る大円と、本初子午線を通る大円とのなす角度で表されます。本初子午線よりも東側を東経、西側を西経と言い、それぞれ0〜180度まであります。緯度は、その地点における天頂の方向と赤道面とのなす角度で表されます。赤道が緯度0度となり、北を北緯、南を南緯といいます。北極・南極の緯度は90度です。地球が球体であるとすれば、緯度と経度は下図のように描くことがことができます。

しかし実際には、地球は厳密には球体とは言えません。地形による凹凸があるだけでなく、自転による遠心力が働くために、赤道半径が極半径よりも大きくなっているからです。

そこで現実の地球を、回転楕円体で近似することを考えます。どのような回転楕円体で近似するか（準拠楕円体¹）を決定する必要があります。そして、その準拠楕円体の上で、地球上の位置を緯度・経度・高度で表すための座標系、すなわち測地座標系を決定する必要があります。つまり、準拠楕円体と測地座標系の組み合わせによって、地球上の任意の地点を、緯度・経度で表現できるのですが、その組み合わせのことを、測地系といいます。

準拠楕円体

ここでは、3つの準拠楕円体を紹介します。

準拠楕円体	赤道半径（m）	扁平率²
ベッセル楕円体	6,377,397.155	1/299.15281285
GRS80	6,378,137	1/298.257222101
WGS84	6,378,137	1/298.257223563

ベッセル楕円体は、地上での測量によって計算された楕円体です。 1841年にドイツの天文学者フリードリヒ・ヴィルヘルム・ベッセルによって導出されました。実は、ベッセル楕円体は実際の地球の形とはかなりズレていましたが、ヨーロッパやロシア・インドなど、ユーラシア大陸での測量結果に基づいていたので、それらの地域で使用するのに都合が良かったと考えられます。

しかし、20世紀後半から、人工衛星や電波望遠鏡などを使う測地技術が進化しました。 1980年に、回転楕円体の正確な形状を国際的に決定したのが、GRS80です。

WGS84はGPSで用いられる回転楕円体ですが、赤道半径や扁平率の数字を見ると、WGS84とGRS80はほぼ等しいことがわかります。実用上は、この2つの回転楕円体は同じものだとして扱っても、ほぼ問題ありません。

測地座標系

日本でよく使われる測地座標系には、2002年以前の（ベッセル楕円体を使った）日本測地系と、それ以降の（GRS80を採用した）世界測地系があります。世界測地系には、世界測地系には、測地成果2000に基づく「日本測地系2000（JGD2000）」と、測地成果2011に基づく「日本測地系2011（JGD2011）」があります。 JGD2011は、2011年の東北地方太平洋沖地震によって生じた地殻変動を考慮した改訂版で、東北地方以外の地域では、JGD2000とJGD2011の差はほとんどありません。また、WGS84は測地座標系の呼称として用いられることもあります。

日本測地系が21世紀初頭まで使われ続けたのはなぜか？

ベッセル楕円体を利用した日本測地系は、実際の地球からはズレていましたが、2002年まで利用されました。その理由としては、日本で測量した結果なので、日本周辺の地図に使用する上では実用上問題なかったこと、経度・緯度は世の中に広く浸透していて簡単に変更できないと思われたこと、などが挙げられます。そのため、測量の基準として、日本測地系は測量法に明記されて使われ続けました。

日本測地系？世界測地系？

JGD2000やJGD2011は、測地座標系としては世界測地系なのですが、測地系としての名称はそれぞれ日本測地系2000と日本測地系2011です。とても紛らわしく、間違えやすいので、気をつけてください。

測地系

繰り返しになりますが、準拠楕円体と測地座標系の組み合わせを測地系といいます。日本でよく使われる測地系として、以下の4つを表にまとめておきます。

測地系	測地座標系	準拠楕円体	EPSG
日本測地系（Tokyo）	日本測地系	ベッセル楕円体	4301
日本測地系2000（JGD2000）	世界測地系（ITRF94座標系³）	GRS80楕円体	4612
日本測地系2011（JGD2011）	世界測地系（ITRF2008座標系	GRS80楕円体	6668
WGS1884（WGS84）	世界測地系（WGS84座標系）	WGS84楕円体	4326

EPSGコード

EPSGコードとは、各座標参照系に固有に割り振られた数字4桁のコードで、 European Petroleum Survey Group（EPSG）が作成し、 International Association of Oil and Gas Production（IOGP）が管理しています。 epsg.io などのウェブサイトで検索することが可能です。データの読み込みや（投影）変換を行うときに、EPSGを知っていると便利です。コードを覚える必要はありませんが、このような仕組みがあることは知っておいてください。

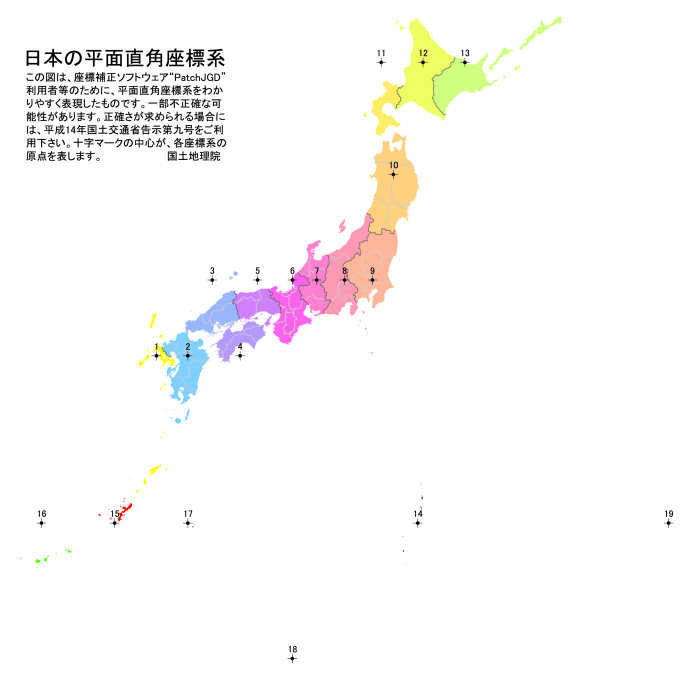
日本測地系（Tokyo）と世界測地系（WGS84）では、どのくらい違っているのでしょうか。明治時代に、当時の東京天文台の経度・緯度が、天文観測により決定されました。この位置が現在の日本経緯度原点となっています。この日本経緯度原点の緯度・経度を、GPSを用いて計測した結果と比較した表を示します。

	緯度	経度
日本測地系（Tokyo）	北緯 35° 39’ 17.5148’’	東経 139° 44’ 45.5020’’
世界測地系（WGS84）	北緯 35° 39’ 29.2’’	東経 139° 44’ 27.9’’

これを見ると、経度が約－12秒、緯度が約＋12秒ほど変化していることがわかります。これを距離に換算すると、北西方向へ約450mずれることに相当します。福岡県付近では、日本測地系と世界測地系のずれは、約420mになります。

投影座標系

測地座標系が決まれば、位置を正確に数値で表すことができます。

次に考えないといけないのは、その位置を、紙の地図やPC画面などの平面で表すにはどうすれば良いかです。距離や面積を使った分析を行うには、緯度・経度のままでは不便ですので、楕円体である地球を、平面に投影する必要があります。その方法を投影法といい、投影された座標を投影座標と呼びます。

ここでは、日本でよく用いられる3つの投影座標系を紹介します。

平面直角座標系

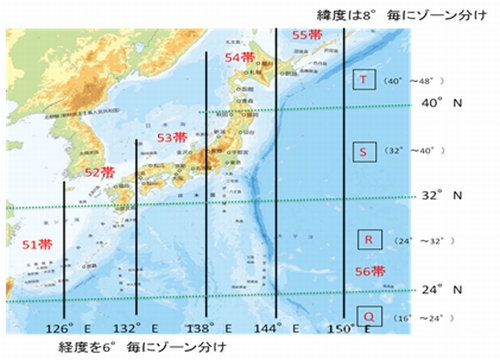
日本全土に19箇所の原点を設定して、それぞれの原点からの距離をXY座標値として扱います。国土地理院発行の国土基本図（縮尺1：2,500〜1：5,000）で使われているほか、公共測量でも利用されるので、公共測量座標系とも呼ばれています。地域がどの原点に対応するかは、基本的には都道府県単位で決められています。

平面直角座標系のEPSGコードは、下表の通りです。

系番号	JGD2000	JGD2011
I	2443	6669
II	2444	6670
III	2445	6671
IV	2446	6672
V	2447	6673
VI	2448	6674
VII	2449	6675
VIII	2450	6676
IX	2451	6677
X	2452	6678
XI	2453	6679
XII	2454	6680
XIII	2455	6681
XIV	2456	6682
XV	2457	6683
XVI	2458	6684
XVII	2459	6685
XVIII	2460	6686
XIX	2461	6687

UTM座標系

UTM図法（ユニバーサル横メルカトル図法：Universal Transverse Mercator Projection）を用いる座標系です。北緯84度から南緯80度の範囲について、経度6ごと毎に地球を60のゾーンに分割し、そのゾーン毎にガウス・クリューゲル図法を適用します。日本が属するゾーンには、51帯〜56帯の6ゾーンがあります。

UTM座標系のEPSGコードは、下表の通りです。

ゾーン	JGD2000	JGD2011
51	3097	6688
52	3098	6689
53	3099	6690
54	3100	6692
55	3101	6693

Webメルカトル

GoogleマップなどのWebの地図で標準的に用いられている座標系です。 WebメルカトルのEPSGコードは、3857です。

測地参照系まとめ

測地系は、準拠楕円体と測地座標系の組み合わせで決まります。

測地参照系は、測地系と投影座標系の組み合わせで決まります。

測地系	測地座標系	準拠楕円体	投影座標系	EPSGコード
Tokyo	日本測地系	ベッセル楕円体	緯度経度	4301
JGD2000	世界測地系	GRS80	緯度経度	4612
JDG2011	世界測地系	GRS80	緯度経度	6668
WGS84	WGS84	WGS84	緯度経度	4326
JGD2000	世界測地系	GRS80	平面直角座標	2443〜2461
JDG2011	世界測地系	GRS80	平面直角座標	6669〜6687
JGD2000	世界測地系	GRS80	UTM座標	3097〜3101
JDG2011	世界測地系	GRS80	UTM座標	6688〜6692
WGS84	WGS84	WGS84	Webメルカトル	3857

RとRStudioのインストール

この講義では、統計解析ソフトRと、その開発環境RStudioを利用します。ここでは、そのインストール方法を説明します。

RStudioを使うにはRが必要ですので、インストールの順序としては、初めにRをインストールし、次にRStudioをインストールします。

Rのインストール

Rは、自由に利用できる統計計算とグラフィックのための言語と環境で、線形および非線形モデリング、統計検定、時系列分析、分類、クラスタリングなど、さまざまな統計およびグラフィックの技術が利用できます。

Rは、CRAN（The Comprehensive R Archive Network）と呼ばれるサイトで公開されています（読み方は、おそらく「シーラン」）。 CRANは世界各地にミラーサイトが開設されており、日本では山形大学によってミラーサイトが提供されています。

以下では、Windows OSの場合を例に、Rをインストールする手順を説明します。 Webブラウザで、いずれかのCRANミラーサイトにアクセスしてください。

[Download R for Windows]をクリックします。

[base]をクリックします。

[Download R-4.*.* for Windows]をクリックすると、ダウンロードが開始されます。

保存されたインストーラをダブルクリックで起動し、その指示に従って、Rをインストールしてください。

RStudioのインストール

RStudioは、Rのための統合開発環境（Integrated Development Environment：IDE）です。 RStudioを使わなくても（Rだけでも）使うことはできるのですが、RStudioがRを使う上でとても便利な環境を提供しているので、この講義ではRStudioを使います。

RStudioはposit社（旧RStudio社）が開発しており、そのデスクトップ版は無料で利用することができます。

以下のリンクから、RStudioのダウンロードサイトにアクセスしてください。

RStudio Desktopダウンロードサイト

[Download RStudio Desktop for Windows]をクリックすると、ダウンロードが開始されます。

保存されたインストーラをダブルクリックで起動し、その指示に従って、RStudioをインストールしてください。

インストールの確認

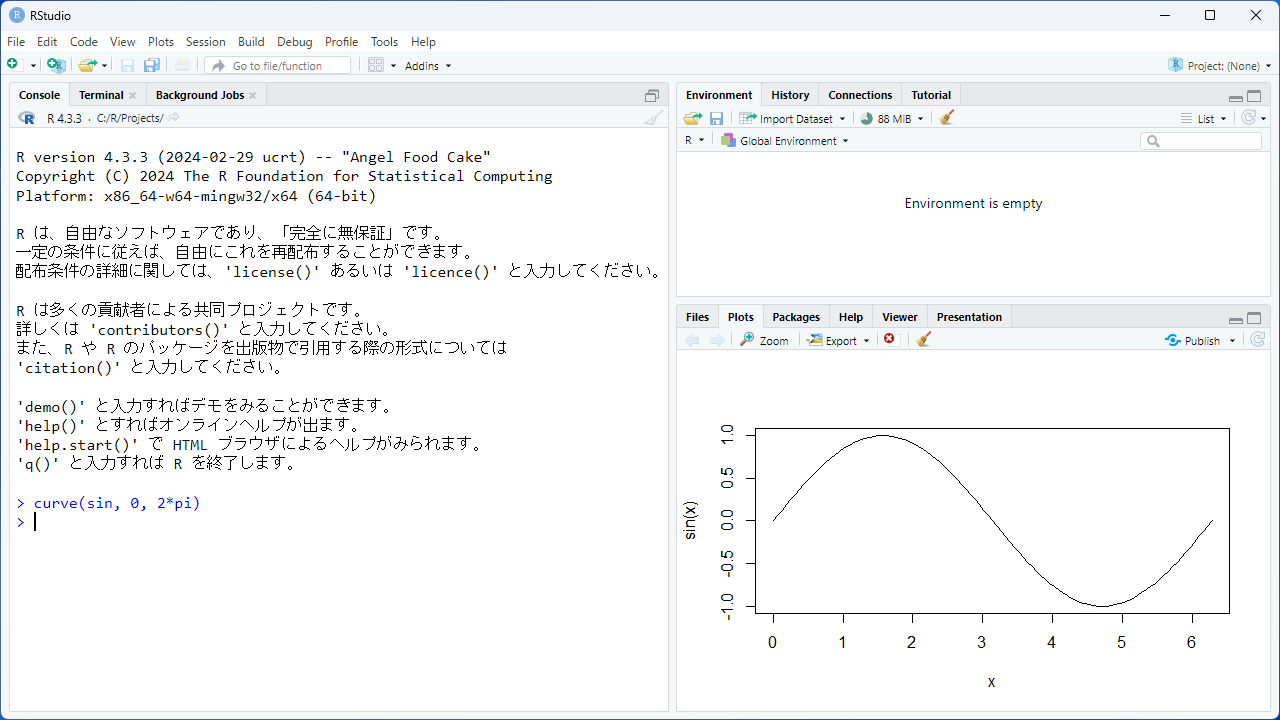
インストールしたRStudioを起動してみましょう。下のような画面が表示されたと思います。

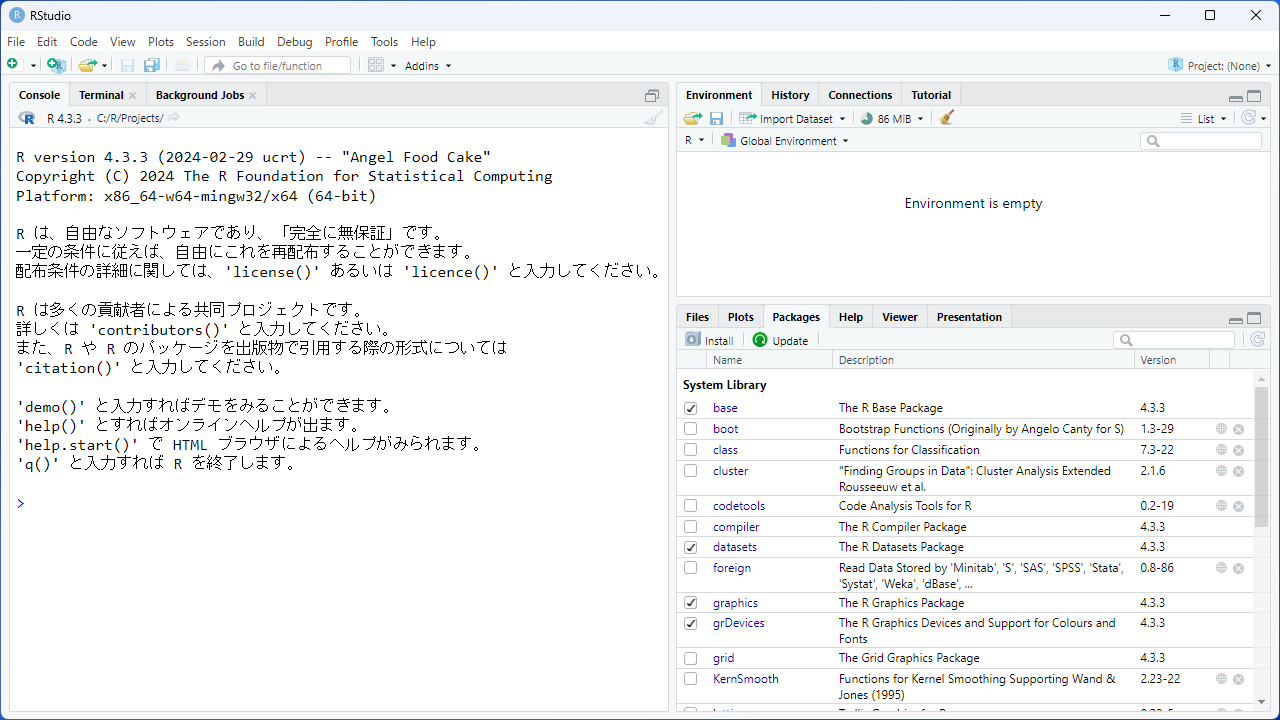
左側のコンソール・ペイン（Console Pane）に、次のように入力して、リターンキーを推してください。

curve(sin, 0, 2*pi)

このように、右下のプロット・ペイン（Plots Pane）にサインカーブが描かれたら、RとRStudioのインストールは、成功しています。

課題

RStudioを使って、以下の手順で画像ファイル（PNGファイル）を作成してください。作成したファイルを、LiveCampusから提出してください（第1回課題：サインカーブの図）

まず、Console Paneに以下のコードを入力してください（” “で囲まれた数字は、それぞれ自分の学籍番号に変えてください）。

curve(sin, 0, 2*pi, main = "12345678")

プロット・ペインにサインカーブの図が描かれると思いますので、この図をPNGファイルとして保存します。

[Export]から[Save as Image…]を選択してください。

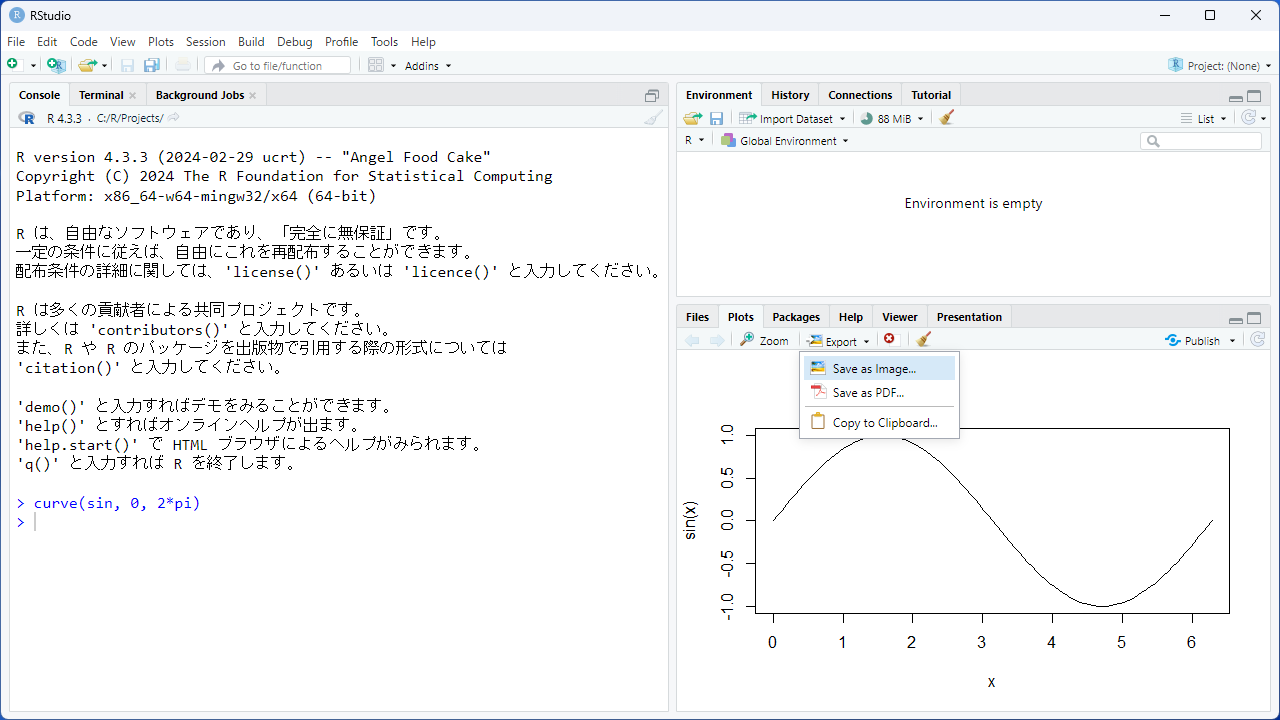
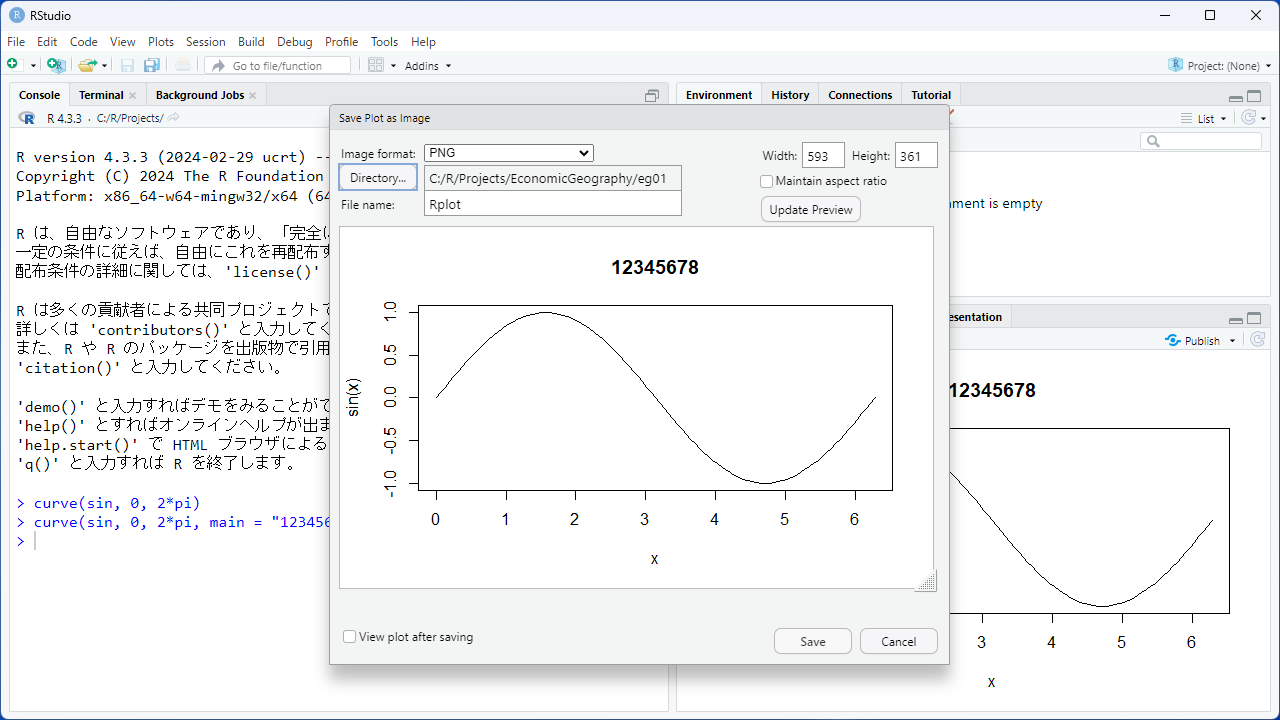
[Directory…]をクリックし、ファイルを保存するディレクトリを設定します。 [Save]ボタンを押すと、指定した場所にPNGファイルが作成されていると思います。

できたファイルを、LiveCampusから提出してください（締切：4月17日14:30）

脚注

地球楕円体を測量の基準にするためには、楕円体の中心を実際の地球上のどの位置に、またその楕円体の軸が実際の地球のどこを通るかということを決める必要があります。このように、位置と方向が決められた地球楕円体を準拠楕円体と呼びます。↩︎
赤道半径と極半径の差を赤道半径で割ったもの。↩︎
ITRF系（International Terrestrial Reference Frame：国際地球基準座標系）は、IERS（International Earth Rotation Service：国際地球回転観測事業）という国際的な学術機関が構築している3次元直交座標系です。↩︎