# パッケージのロード
library(tidyverse)
library(readxl)
library(sf)
library(jpgrid)
library(units)10: 距離分布・ボロノイ図
はじめに
今回も、これまでの講義内容の復習を兼ねて、Rを使った立地分析の演習を行います。 今日の演習では、いろいろな空間データをつかって、福岡県柳川市の小学校の統廃合について考えてみることにします。
今日の演習では以下の5つのパッケージを使用します(unitsパッケージは明示的に使うわけではありませんが、距離に関するグラフを描く際に必要なので、あらかじめロードしておきます)。
小学校の再編
日本は人口減少社会に突入し、さまざまな公共施設・公共サービスの見直しが行われています。 義務教育のための施設である小中学校についても、その例外ではありません。
2000年以降、文部科学省を中心に「公立小学校・中学校の適正規模・適正配置」が政策として推進されており、 福岡県柳川市でも、2010年頃から小中学校の統廃合の検討を進めました。
柳川市立小中学校再編計画によると、計画を策定した2022年現在で19校ある小学校と6校ある中学校を、統廃合によって5校の小学校と2校の中学校、そして2校の義務教育学校(小中一貫校)に再編する計画になっています。 また、新しい学校の通学区域(校区)は、現行の校区を分割せず、現在の学校の校区単位の組み合わせによって再編することとしています。
今回の演習では、柳川市の小学校の統廃合について、特に学校までの距離に着目して分析してみます。
小学校区の可視化
現在および計画されている将来の小学校区を地図に表示してみましょう。 まずはデータを国土数値情報からダウンロードします。 福岡県の小学校区データ(ポリゴン)と学校データ(ポイント)をそれぞれダウンロードしてください。
ダウンロードしたファイルを展開し、できたフォルダを今日のプロジェクトのdataフォルダに移動してください。
まず、sf::st_read関数を使って小学校区データを読み込みましょう。
# 小学校区データの読み込み
district <- st_read("data/A27-23_40_GML/A27-23_40.geojson") |>
st_transform(6670)Reading layer `A27-23_40' from data source
`/Users/kzktmr/Documents/LectureNotes/EconomicGeography/data/A27-23_40_GML/A27-23_40.geojson'
using driver `GeoJSON'
Simple feature collection with 371 features and 5 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 130.3394 ymin: 32.99997 xmax: 131.2472 ymax: 33.91904
Geodetic CRS: JGD2011次いで、学校データも読み込みます。 学校データは、幼稚園から大学まで、学校教育法で規定される全ての学校のデータが含まれていますので、その中から小学校のデータだけをフィルタリングで抽出します。 ここでは、dplyr::filter関数を使って、学校分類コード(P29_003)が小学校(16001)であるデータを抜き出しています。
# 学校データの読み込みと小学校データの抽出
location <- st_read("data/P29-23_40_GML/P29-23_40.geojson") |>
filter(P29_003 == 16001) |> st_transform(6670)Reading layer `P29-23_40' from data source
`/Users/kzktmr/Documents/LectureNotes/EconomicGeography/data/P29-23_40_GML/P29-23_40.geojson'
using driver `GeoJSON'
Simple feature collection with 2027 features and 9 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 130.0358 ymin: 33.0043 xmax: 131.1882 ymax: 33.99282
Geodetic CRS: JGD2011福岡県の小学校区と小学校を地図に重ねて表示してみましょう。
# 福岡県の小学校区地図
ggplot() +
geom_sf(data = district) +
geom_sf(data = location) +
theme_minimal()
図を見ると、福岡市や北九州市をはじめとして、校区データが掲載されていない地域も少なくないことがわかります。 また、小学校区データの説明には、「本データは十分な精度や正確性をもったものではなく、利用にあたっては公式な資料としては扱えないなど、注意が必要である」との記載があるとおり、利用目的によってはこのデータは使えませんので、注意してください(今回の演習での分析内容では、問題なく使えます)。
それぞれのデータについて、filter関数を使って、柳川市(自治体コード:40207)のデータだけを抽出しましょう。
# 柳川市のデータを抽出
district <- district |>
filter(A27_001 == "40207") |> select(school = A27_004)
glimpse(district)Rows: 19
Columns: 2
$ school <chr> "東宮永小学校", "矢留小学校", "城内小学校", "柳河小学校", "中山小学校", "垂見小学校", "二ッ河小学…
$ geometry <MULTIPOLYGON [m]> MULTIPOLYGON (((-54688.69 1..., MULTIPOLYGON (((…location <- location |>
filter(P29_001 == "40207") |>
mutate(school = str_remove(P29_004, "^柳川市立")) |>
select(school)
glimpse(location)Rows: 19
Columns: 2
$ school <chr> "柳河小学校", "城内小学校", "矢留小学校", "昭代第二小学校", "皿垣小学校", "有明小学校", "中島小学…
$ geometry <POINT [m]> POINT (-55116.49 18866.97), POINT (-55422.91 18064.95),…それぞれ、学校名以外のデータは使用しないので削除しています。 また、ポイントデータの学校名から「柳川市立」という文字列を取り除いています。
柳川市の小学校と小学校区を地図に重ねて表示します。
# 柳川市の小学校区地図(2023年)
ggplot() +
geom_sf(data = district) +
geom_sf(data = location) +
theme_minimal()
人口分布
人口分布は、5次メッシュ(250mメッシュ)を使ってみましょう。 前回と同様に、jpgirdパッケージを使ってメッシュポリゴンを準備します。
柳川市にかかるメッシュポリゴンを作成するために、柳川市域のポリゴンデータが必要です。 今回は、小学校区のポリゴンデータがあるので、これをsf::st_union関数で統合することで、 柳川市のポリゴンを作りましょう。
# 柳川市域のポリゴンを作成
yngw_city <- st_union(district)
ggplot() + geom_sf(data = yngw_city) +
theme_minimal()
前回の演習と同様に、 jpgrid::geometry_to_grid関数とjpgrid::grid_as_sf関数を組み合わせて、 柳川市の250 mメッシュポリゴンを作成します。
# 柳川市の250mメッシュポリゴンの作成
yngw_grid <-
yngw_city |> st_transform(6668) |>
geometry_to_grid(grid_size = "250m") |> first() |>
grid_as_sf(crs = 6668) |> st_transform(6670) |>
mutate(meshcode = as.character(grid))メッシュポリゴンを地図に表示すると、次のようになります。
# 柳川市250mメッシュの表示
ggplot() + geom_sf(data = yngw_grid) +
theme_minimal()
次に統計データをダウンロードするわけですが、柳川市は1次メッシュコード4930の範囲に収まっていることを確認しておきましょう。
# 柳川市の1次メッシュコードが4930であることの確認
yngw_grid |> pull(meshcode) |> str_starts('4930') |> all()[1] TRUE人口データはe-Statからダウンロードしてください。
- 統計データダウンロード
- [国勢調査]→[2020年]→[5次メッシュ(250mメッシュ)]→[人口移動、就業状態等及び従業地・通学地(JGD2011)]→[都道府県で絞込み(福岡県)]→[M 4930]
- ダウンロードページへのダイレクトリンクはこちら
tblT001145Q4930.zipがダウンロードされると思いますので、すべて展開してください。 展開してできたフォルダの中にあるtblT001145Q4930.txtをプロジェクトのdataフォルダに移動してください。
readr::read_csv関数を使ってtblT001145Q4930.txtを読み込みます。 例によって、2回に分けて読み込むことにします。
ここでは、空白および秘匿データ(*)を欠損値として処理しています。 また、KEY_CODEとT001145037(在学者 うち 小学校・中学校 総数)を取り出し、ぞれぞれmeshcodeとstudentと名前をつけておきます。 さらに、meshcodeを数値型から文字列型に変更しておきます。
# メッシュ統計データの読み込み
col_names <-
read_csv('data/tblT001145Q4930.txt', n_max = 1,
col_names = FALSE, col_types = 'c',
locale = locale(encoding = 'cp932')) |>
as.character()
population <-
read_csv('data/tblT001145Q4930.txt', skip = 2,
col_names = col_names, na = c("", "*")) |>
select(meshcode = KEY_CODE, student = T001145037) |>
mutate(meshcode = as.character(meshcode))Rows: 32215 Columns: 98
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): GASSAN
dbl (97): KEY_CODE, HTKSYORI, HTKSAKI, T001145001, T001145002, T001145003, T...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.glimpse(population)Rows: 32,215
Columns: 2
$ meshcode <chr> "4930010022", "4930010023", "4930010024", "4930010034", "4930…
$ student <dbl> NA, 4, 5, NA, 2, 5, NA, 0, 0, NA, NA, 11, 3, 0, 7, NA, 6, 1, …読み込んだ人口データを、メッシュポリゴンに結合します。
# メッシュポリゴンデータに統計データを結合
yngw_grid <- yngw_grid |>
left_join(population, by = join_by(meshcode)) 小中学校の在学者数で色を塗ったメッシュ地図を描いてみましょう。
# 柳川市の小中学校在学者数地図
ggplot() +
geom_sf(aes(fill = student), data = yngw_grid) +
scale_fill_distiller(direction = 1) +
theme_minimal()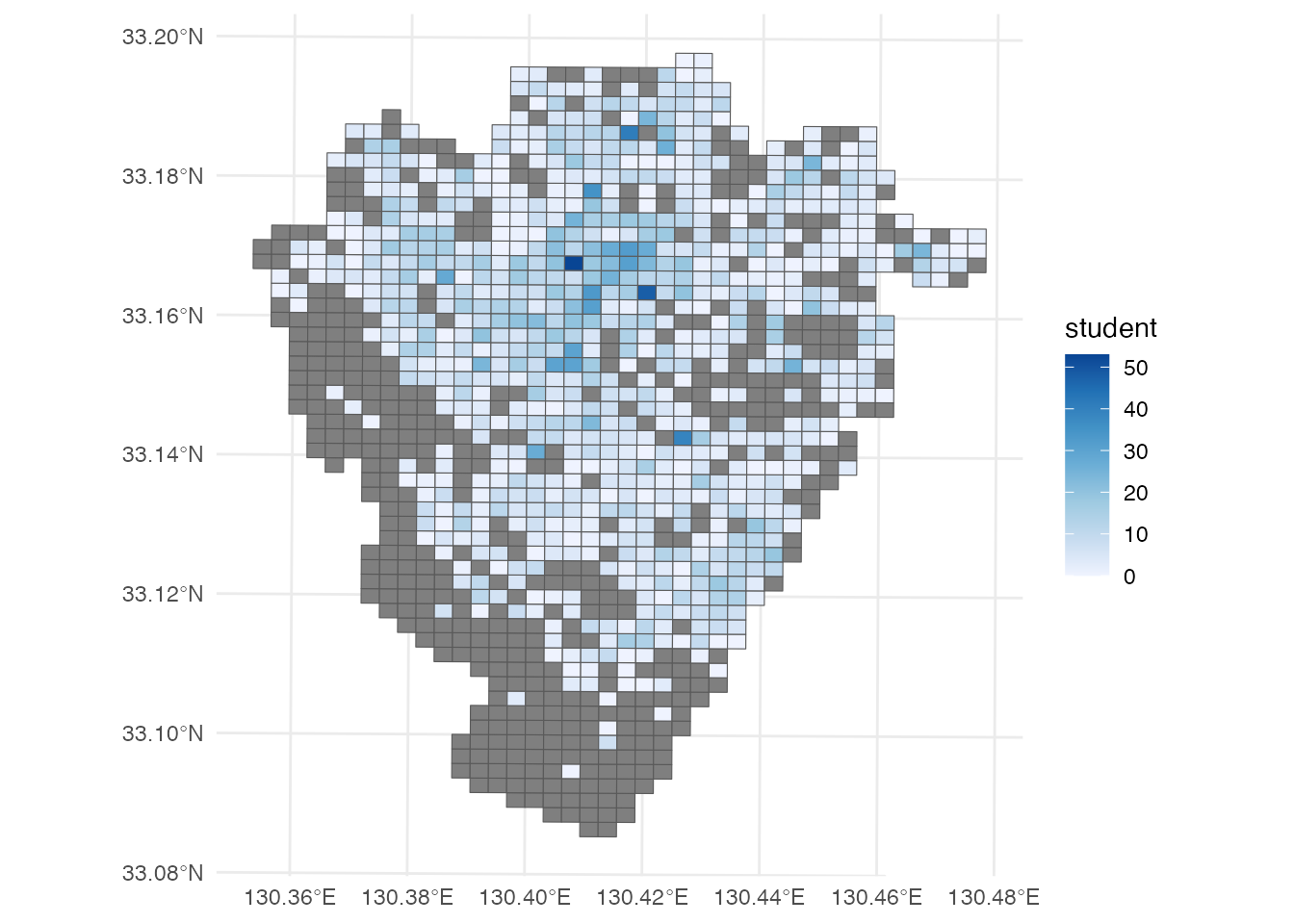
学校ごとの児童数の推計
250mメッシュの人口データを使って分析するわけですが、 このデータは、実際の小学生の人口分布とのずれがあります。 ずれの理由は、(1)人口がメッシュに集約されていることの誤差と、(2)小学生のみのデータではなく小・中学生の合計の人数を使っていることによる誤差です。
ここで、その誤差による影響を確認するために、メッシュ人口を小学校区で集計して、 実際の学校ごとの児童数と比較してみます。
実際の児童数は、 柳川市の小学校の統廃合についてExcelファイルに整理した以下のファイルから入手しましょう。 次のリンクから「yanagawa_es_reog.xlsx」をダウンロードし、dataフォルダに格納してください。
readxl::read_excel関数で読み込みます。
# 柳川市小学校再編データ
reog_data <- read_excel('data/yanagawa_es_reog.xlsx')「yanagawa_es_reog.xlsx」の中身は、以下のようになっています。 全部で19行のデータがあり、1列目が現在の学校名「school」、2列目が再編後の学校名「future_school」、 そして3列目が2021年度の各校の児童数「student」です1。
| school | future_school | student |
|---|---|---|
| 柳河小学校 | 柳城小学校 | 207 |
| 城内小学校 | 柳城小学校 | 187 |
| 東宮永小学校 | 柳城小学校 | 173 |
| 矢留小学校 | 柳南小学校 | 200 |
| 両開小学校 | 柳南小学校 | 160 |
| 昭代第一小学校 | 昭代学校 | 211 |
| 昭代第二小学校 | 昭代学校 | 206 |
| 蒲池小学校 | 蒲池学校 | 312 |
| 皿垣小学校 | 大和小学校 | 60 |
| 有明小学校 | 大和小学校 | 75 |
| 中島小学校 | 大和小学校 | 163 |
| 六合小学校 | 大和小学校 | 127 |
| 大和小学校 | 大和小学校 | 100 |
| 豊原小学校 | 大和小学校 | 160 |
| 藤吉小学校 | 藤吉小学校 | 405 |
| 矢ヶ部小学校 | 三橋小学校 | 110 |
| 二ッ河小学校 | 三橋小学校 | 188 |
| 垂見小学校 | 三橋小学校 | 157 |
| 中山小学校 | 三橋小学校 | 63 |
さて、メッシュ人口を小学校区で集計するわけですが、そのために、まず、メッシュ(ポリゴン)データを、 代表点のポイントデータへと変換します(sf::st_centroid関数を使ってポリゴン重心を代表点にします)。 次に、校区データにポリゴン重心のポイントデータをsf::st_join関数を使って空間結合し、group_by関数とsummarise関数を使って、校区ごとにメッシュ人口を集計します。 その際に、小中学生に占める小学生の比率を2/3として推計することにし、これをestimated列として追加します。 最後に、reog_dataにある児童数を利用するために、left_joinで結合します。
# メッシュデータをポイントデータに変換
grid_pop <- yngw_grid |> st_centroid()Warning: st_centroid assumes attributes are constant over geometries# メッシュデータから学校ごとの児童数を推計
school_pop <- district |>
st_join(grid_pop) |>
group_by(school) |>
summarise(estimated = sum(student, na.rm = TRUE) * (2/3)) |>
left_join(reog_data, by = join_by(school))メッシュデータから推計した学校児童数(estimated)と、実際の児童数(student)の散布図を書いてみます。
# 児童数の推計結果
ggplot(school_pop) +
geom_point(aes(x = student, y = estimated)) +
geom_abline(slope = 1, intercept = 0, color = 'red') +
theme_minimal()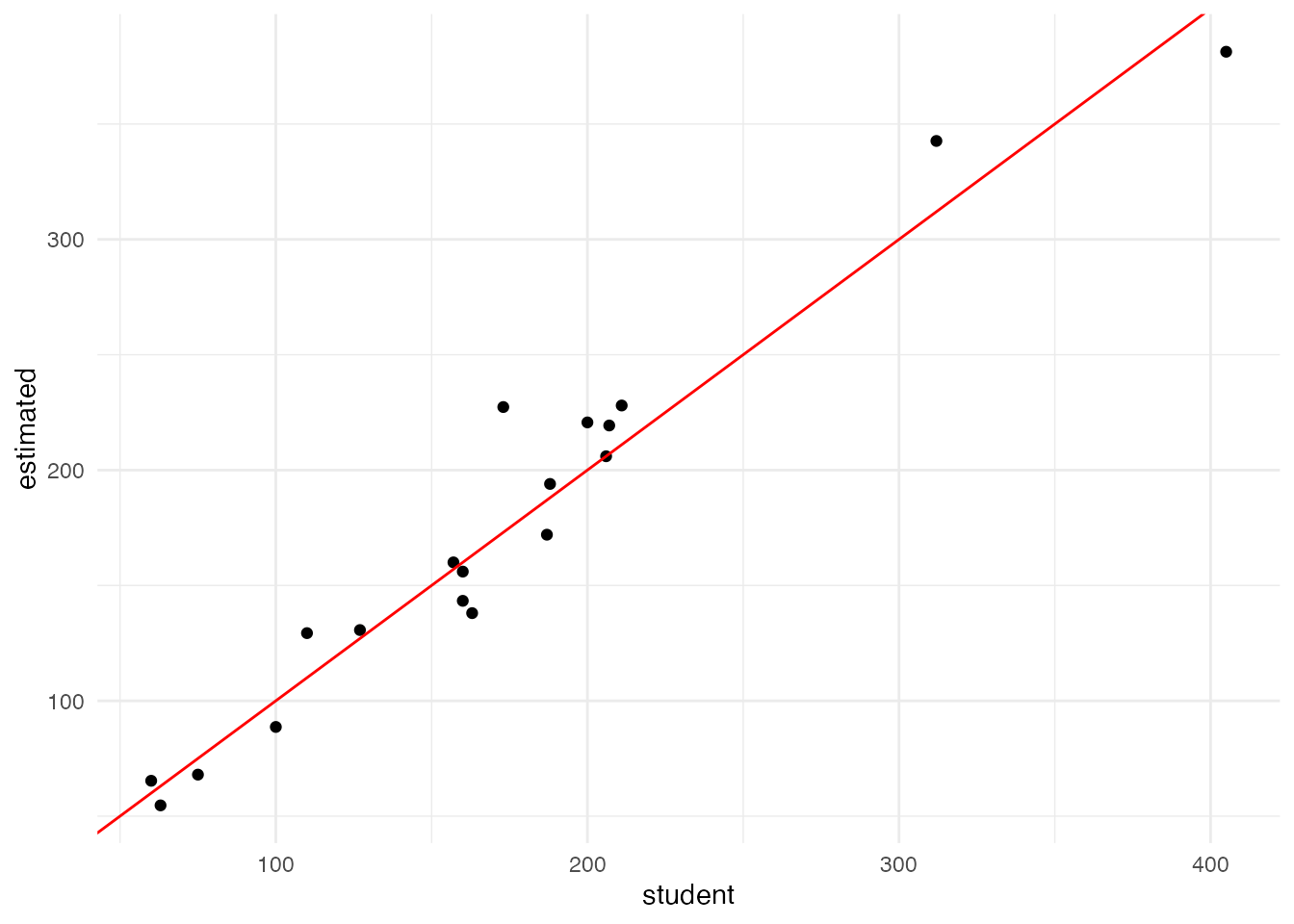
赤い線は、切片0、傾き1の直線(いわゆる45度線)です。 各学校の児童数と推計値が完全に一致すれば、プロットされた点は、この線の上にピッタリ重なります。 図を見ると、19ある小学校の点はほぼ45度線に沿っていて、 良い精度でメッシュ人口から学校ごとの児童数を推定できている、と言えそうです。
距離分布
次に、各メッシュから、校区の小学校までの距離を計測して、生徒の通学距離の分布がどのようになっているのか調べましょう。 そのためには、各メッシュがどの校区に存在するかを調べる必要があります。 この目的のためには、空間結合が使えますね。
準備として、分析対象とするメッシュを、その図形代表点が市域に含まれるものだけにしておきます。 また、人口データがNAでないメッシュだけにしておきます。
# 代表点が市域に含まれ、かつ人口がNAでないメッシュだけを抽出
grid_pop <- grid_pop |>
st_filter(yngw_city) |>
filter(!is.na(student))
glimpse(grid_pop)Rows: 723
Columns: 4
$ grid <grd250> 4930531223, 4930531333, 4930532311, 4930532324, 4930532142…
$ geometry <POINT [m]> POINT (-55277.44 10667.83), POINT (-54691.45 11126.63),…
$ meshcode <chr> "4930531223", "4930531333", "4930532311", "4930532324", "4930…
$ student <dbl> 0, 7, 0, 0, 3, 0, 3, 3, 0, 0, 3, 0, 1, 0, 0, 2, 6, 9, 0, 1, 1…次に、小学校の座標データを加工して、座標データ(geometery)をデータ列に持つようなデータフレームにします。 ただし、st_drop_geometry関数によって、ポイントデータではないただのデータフレームにしている点に注意してください。
# 学校の座標データの加工
school_location <- location |>
mutate(school_geometry = st_geometry(location)) |>
st_drop_geometry()
glimpse(school_location)Rows: 19
Columns: 2
$ school <chr> "柳河小学校", "城内小学校", "矢留小学校", "昭代第二小学校", "皿垣小学校", "有明小学校"…
$ school_geometry <POINT [m]> POINT (-55116.49 18866.97), POINT (-55422.91 180…メッシュ人口データに小学校区のデータを空間結合します。 これで、それぞれのメッシュがどの小学校区に存在するかがわかります。
# メッシュデータに校区の小学校座標データを結合
grid_pop <- grid_pop |>
st_join(district)
glimpse(grid_pop)Rows: 723
Columns: 5
$ grid <grd250> 4930531223, 4930531333, 4930532311, 4930532324, 4930532142…
$ geometry <POINT [m]> POINT (-55277.44 10667.83), POINT (-54691.45 11126.63),…
$ meshcode <chr> "4930531223", "4930531333", "4930532311", "4930532324", "4930…
$ student <dbl> 0, 7, 0, 0, 3, 0, 3, 3, 0, 0, 3, 0, 1, 0, 0, 2, 6, 9, 0, 1, 1…
$ school <chr> "有明小学校", "有明小学校", "有明小学校", "中島小学校", "有明小学校", "有明小学校", "有明小学校"…小学校の名前を使って、小学校の座標データをleft_joinします。 これで、このgrid_popデータには、メッシュ座標と小学校区の座標の2つの座標を持つデータフレームになりました(ただし、ポイントデータとしての座標はメッシュ座標であって、小学校の座標はあくまでもデータフレームの1つのデータ列にすぎません)。
# メッシュデータに校区の小学校座標データを結合
grid_pop <- grid_pop |>
left_join(school_location, by = join_by(school))
glimpse(grid_pop)Rows: 723
Columns: 6
$ grid <grd250> 4930531223, 4930531333, 4930532311, 4930532324, 493…
$ geometry <POINT [m]> POINT (-55277.44 10667.83), POINT (-54691.45 111…
$ meshcode <chr> "4930531223", "4930531333", "4930532311", "4930532324"…
$ student <dbl> 0, 7, 0, 0, 3, 0, 3, 3, 0, 0, 3, 0, 1, 0, 0, 2, 6, 9, …
$ school <chr> "有明小学校", "有明小学校", "有明小学校", "中島小学校", "有明小学校", "有明小学校", …
$ school_geometry <POINT [m]> POINT (-54174.45 13159.02), POINT (-54174.45 131…メッシュ代表点と学校との距離をsf::st_distanceを使って計測します。 計測した距離を、dplyr::mutate関数を使って、新しいデータ列school_distanceとして追加します。
# 各メッシュから校区の学校までの距離を計算
grid_pop <- grid_pop |>
mutate(school_distance = st_distance(geometry, school_geometry, by_element = TRUE))
glimpse(grid_pop)Rows: 723
Columns: 7
$ grid <grd250> 4930531223, 4930531333, 4930532311, 4930532324, 493…
$ geometry <POINT [m]> POINT (-55277.44 10667.83), POINT (-54691.45 111…
$ meshcode <chr> "4930531223", "4930531333", "4930532311", "4930532324"…
$ student <dbl> 0, 7, 0, 0, 3, 0, 3, 3, 0, 0, 3, 0, 1, 0, 0, 2, 6, 9, …
$ school <chr> "有明小学校", "有明小学校", "有明小学校", "中島小学校", "有明小学校", "有明小学校", …
$ school_geometry <POINT [m]> POINT (-54174.45 13159.02), POINT (-54174.45 131…
$ school_distance [m] 2724.4535 [m], 2097.1239 [m], 1873.7285 [m], 2398.4239 […この新しいデータフレームを使って、メッシュから学校までの距離の平均値を計算しましょう。
mean_dist_school <-
weighted.mean(x = grid_pop$school_distance, w = grid_pop$student)
mean_dist_school728.7196 [m]平均距離は約729 mという結果になりました。
生徒数の重みつきヒストグラムを描いてみましょう。
# 通学距離のヒストグラム
ggplot(grid_pop) +
aes(x = school_distance, weight = student) +
geom_histogram(boundary = 0, binwidth = 200,
color = grey(0.2), fill = grey(0.8)) +
geom_vline(xintercept = mean_dist_school, linetype = "dashed") +
theme_minimal()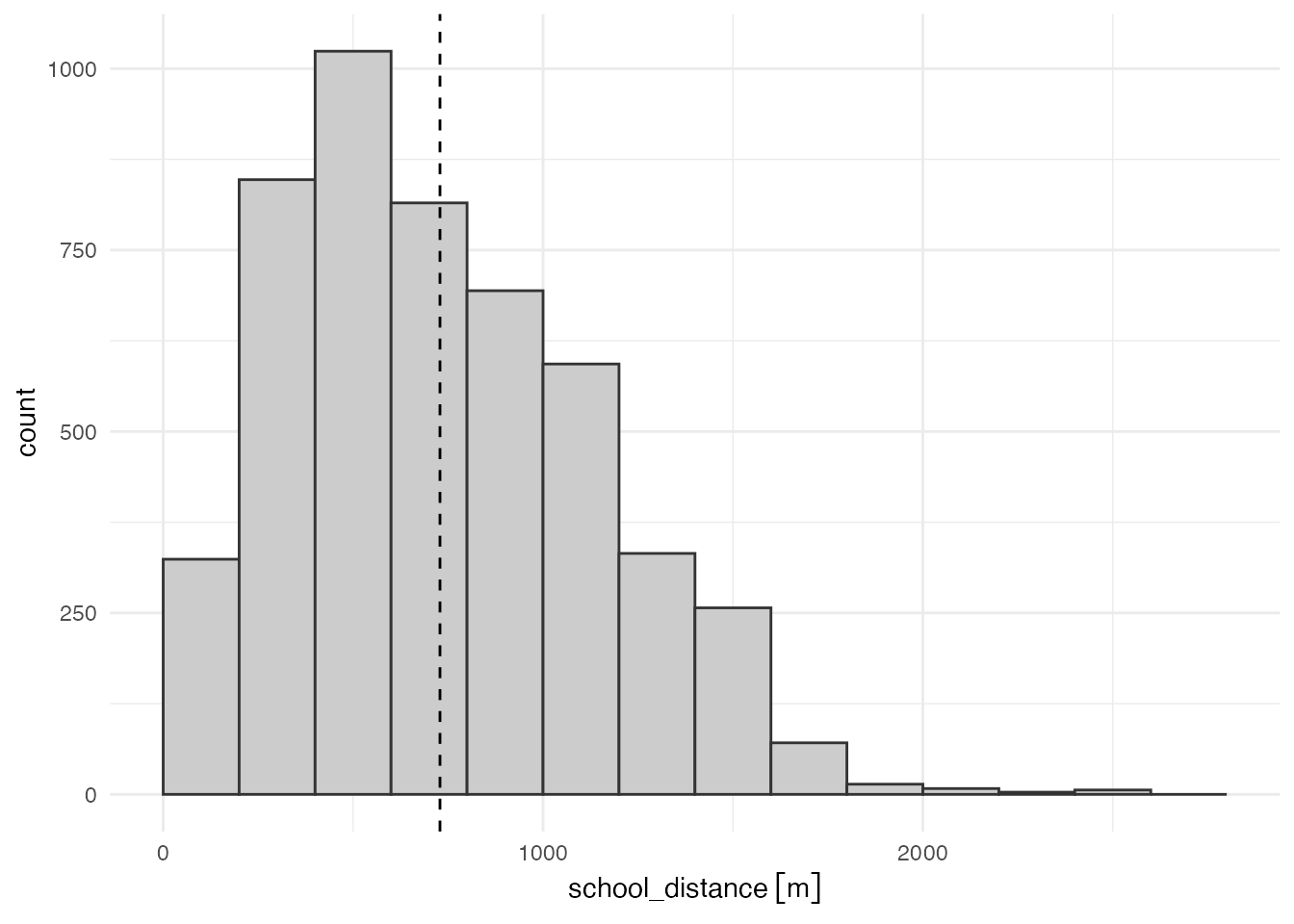
通学距離の累積分布を図にしてみましょう。 これは、通学距離の短い順番にメッシュデータを並べ替えて、その順序で累積した児童数を計算すれば良いです。
# 通学距離の累積分布
school_distance <- grid_pop |>
arrange(school_distance) |>
mutate(count = cumsum(student))
ggplot(school_distance) +
aes(x = school_distance, y = count / sum(student)) +
geom_line() +
geom_vline(xintercept = mean_dist_school, linetype = "dashed") +
scale_y_continuous(name = "cumulative ratio", labels = scales::percent) +
theme_minimal()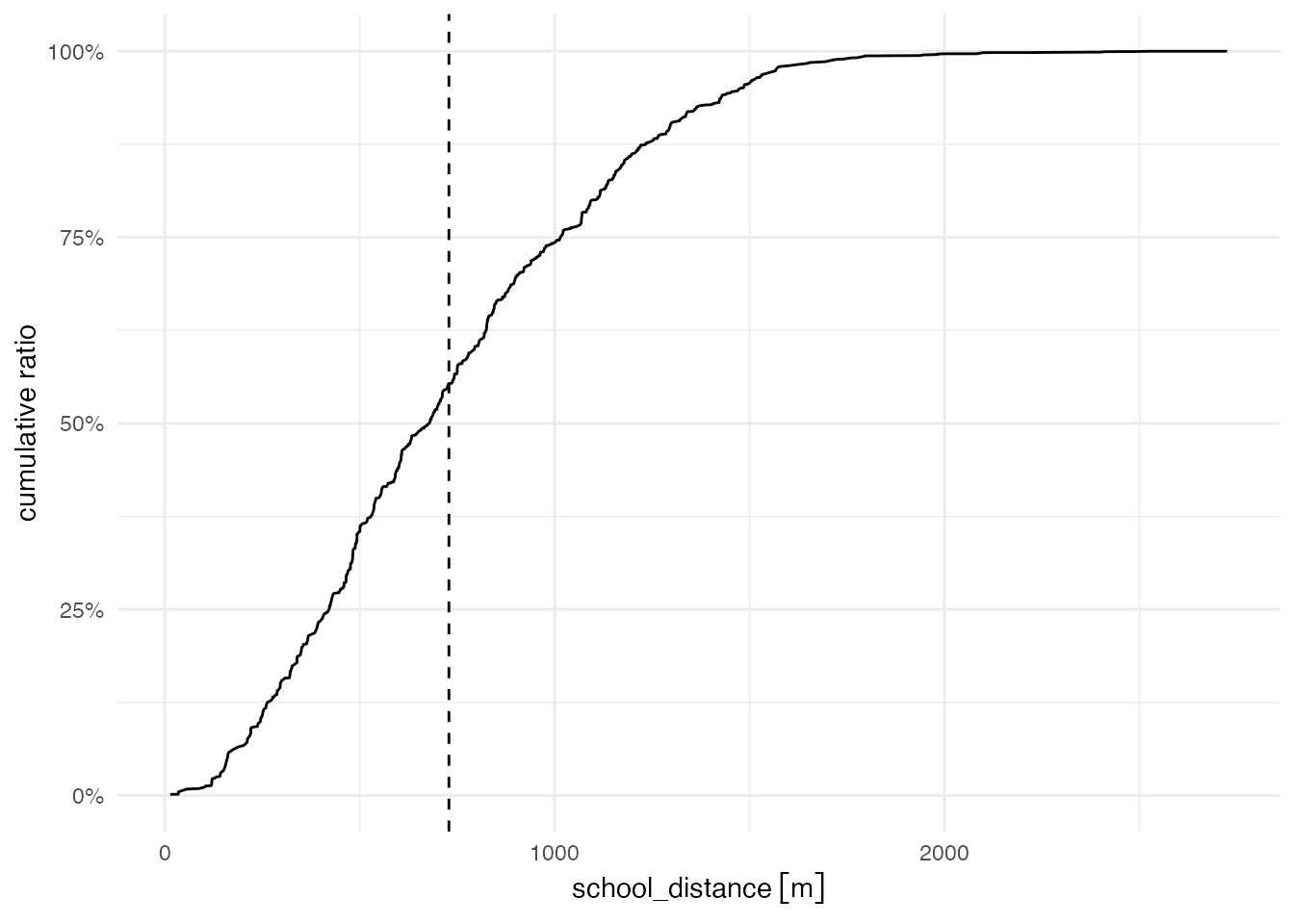
およそ75%の児童の通学距離は1 km未満で、 学校までの直線距離が2 kmを超える児童の割合はとても少ない(計算すると0.4%程度)ことがわかります。
ボロノイ図
空間上に同種とみなすことができる点が複数分布しているとき、 それぞれを最寄りの点とする領域として空間を分割する操作を、ボロノイ分割と呼びます。 そして、ボロノイ分割によって得られた図形全体をボロノイ図と呼びます。
この演習では、小学校を母点として、柳川市を最寄りの小学校によって空間的に分割する操作を考えます。 Rでは、sf::st_voronoi関数でボロノイ分割を実行することができます。
# ボロノイ図の作成
voronoi <- location |>
st_union() |> st_voronoi() |>
st_collection_extract(type = "POLYGON") |>
st_intersection(yngw_city) |> st_sf() |>
st_join(location) |>
rename(voronoi_school = school)sfパッケージの関数をたくさん利用しています。 まず初めに、小学校のポイントデータであるschoolに対して、 sf::st_union関数を使って、sfc_MULTIPOINTに変換しています。 この操作によってできたオブジェクトをsf::st_voronoi関数に入力として与えると、ボロノイ図が作成されます。 この結果から、sf::st_collection_extract関数によってポリゴンを取り出し、 sf::st_sf関数でsfオブジェクトに変換します。 最後に小学校のポイントデータであるschoolを再びsf::st_joinで空間結合して、それぞれのボロノイ領域がどの小学校に対応する領域なのかがわかるようにしています。
それでは、小学校を母点とするボロノイ図を、小学校区と合わせて表示してみましょう。
# 校区とボロノイ領域の重ね合わせ
ggplot() +
geom_sf(data = district) +
geom_sf(data = voronoi, fill = NA, linetype = 'dashed') +
geom_sf(data = location) +
theme_minimal()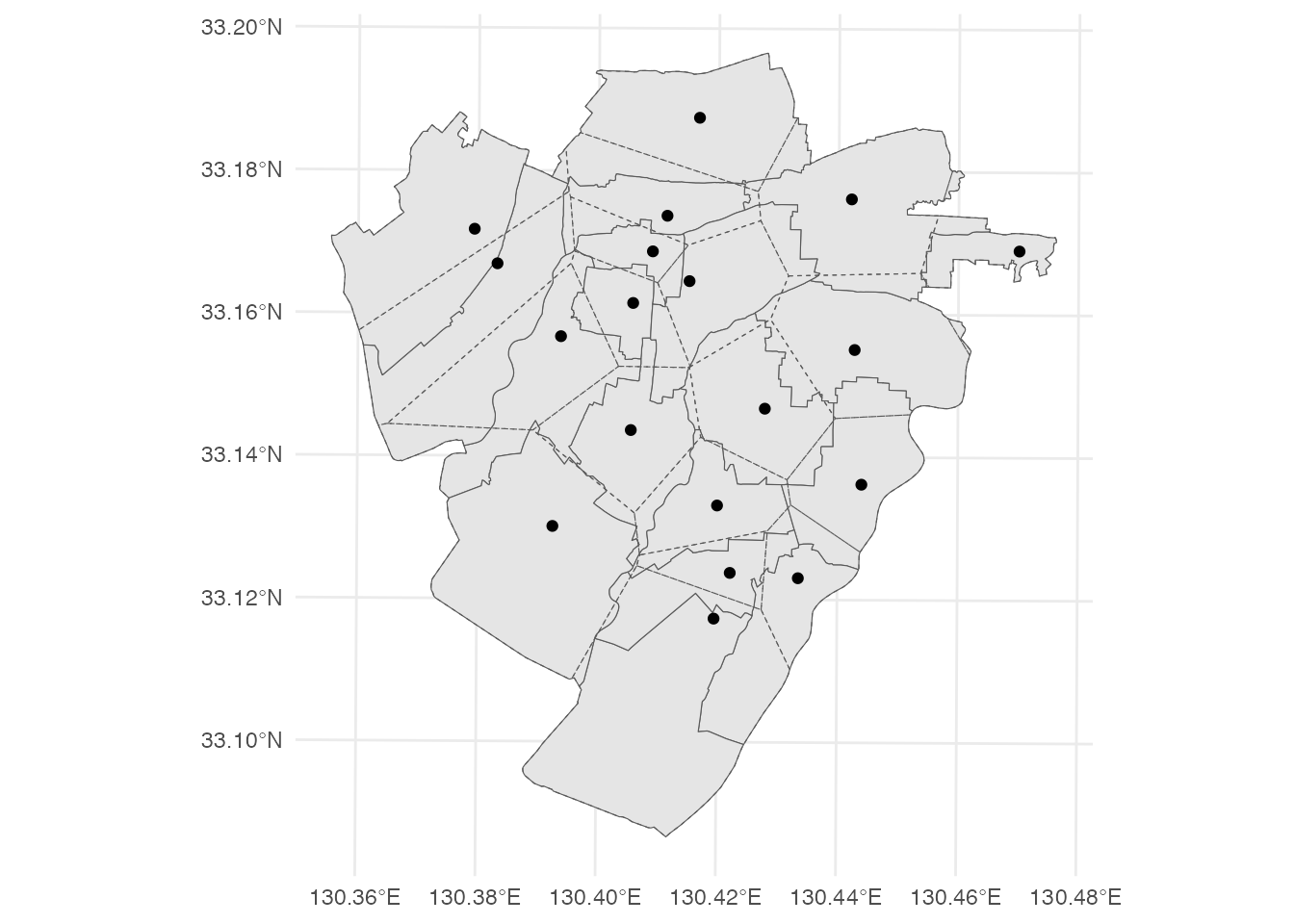
実線で描かれた小学校区と、破線で描かれたボロノイ図は、おおよそ似た形をしていますが、細かいところを見ると、一致しているわけではありません。 両者の成り立ちを考えれば、もちろん一致することはないのですが、どの程度一致しているのかを見ることには、意味があるかもしれません。
小学校区とボロノイ図との乖離の程度見るために、sf::st_intersection関数を使って両者の交差を求め、校区の小学校とボロノイ領域の母点の小学校が異なる領域を抽出します。
# 校区とボロノイ領域の交差
difference <-
st_intersection(district, voronoi) |>
filter(school != voronoi_school)Warning: attribute variables are assumed to be spatially constant throughout
all geometriesこの領域は、いわば、直線距離で見ればもっと近い小学校があるにもかかわらず、その小学校に通学することができない地域であることを意味します。 そのような地域を地図に表示してみましょう。
ggplot() +
geom_sf(data = yngw_city) +
geom_sf(data = difference, fill = 'orange') +
theme_minimal()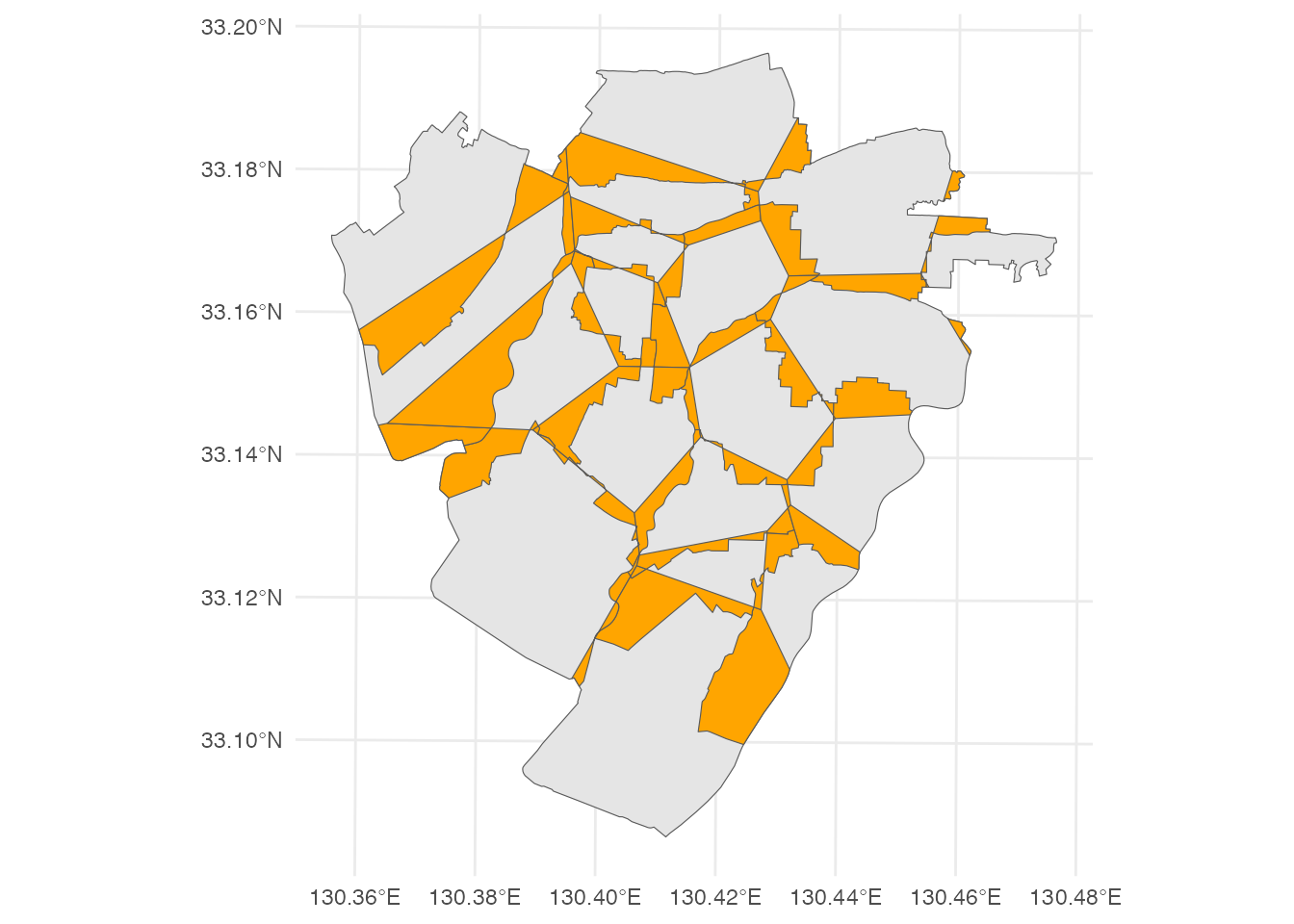
このオレンジ色で塗られた領域の、市域に対する面積比率を求めてみましょう。
# 交差部分の面積比率
sum(st_area(difference)) / st_area(yngw_city) * 10023.36128 [1]約23.4%です。思ったよりも多いな、と感じたかもしれません。
では、この「最も近い小学校に通えないことが通学距離に与える影響」を見積もってみましょう。 先ほど、小学校区のポリゴンデータを使って、学校までの距離の分布と平均を計算しました。 小学校区のポリゴンデータの代わりに、ボロノイ領域のポリゴンデータを使って、同じ計算をした上で、両者を比較すれば良さそうです。
先ほどと同様に、学校のポイントデータを作成しておきます。
# 学校の座標データの加工
voronoi_location <- location |>
mutate(voronoi_geometry = st_geometry(location)) |>
st_drop_geometry() |>
rename(voronoi_school = school)
glimpse(voronoi_location)Rows: 19
Columns: 2
$ voronoi_school <chr> "柳河小学校", "城内小学校", "矢留小学校", "昭代第二小学校", "皿垣小学校", "有明小学校…
$ voronoi_geometry <POINT [m]> POINT (-55116.49 18866.97), POINT (-55422.91 18…# ボロノイ分割による通学距離
grid_pop <- grid_pop |>
st_join(voronoi) |>
left_join(voronoi_location, by = join_by(voronoi_school)) |>
mutate(voronoi_distance = st_distance(geometry, voronoi_geometry, by_element = TRUE))
glimpse(grid_pop)Rows: 723
Columns: 10
$ grid <grd250> 4930531223, 4930531333, 4930532311, 4930532324, 49…
$ geometry <POINT [m]> POINT (-55277.44 10667.83), POINT (-54691.45 11…
$ meshcode <chr> "4930531223", "4930531333", "4930532311", "4930532324…
$ student <dbl> 0, 7, 0, 0, 3, 0, 3, 3, 0, 0, 3, 0, 1, 0, 0, 2, 6, 9,…
$ school <chr> "有明小学校", "有明小学校", "有明小学校", "中島小学校", "有明小学校", "有明小学校",…
$ school_geometry <POINT [m]> POINT (-54174.45 13159.02), POINT (-54174.45 13…
$ school_distance [m] 2724.4535 [m], 2097.1239 [m], 1873.7285 [m], 2398.4239 …
$ voronoi_school <chr> "有明小学校", "有明小学校", "有明小学校", "有明小学校", "有明小学校", "有明小学校",…
$ voronoi_geometry <POINT [m]> POINT (-54174.45 13159.02), POINT (-54174.45 13…
$ voronoi_distance [m] 2724.4535 [m], 2097.1239 [m], 1873.7285 [m], 1615.9226 …ボロい領域による平均値距離を計算してみます。
# 平均距離の計算
mean_dist_voronoi <-
weighted.mean(x = grid_pop$voronoi_distance, w = grid_pop$student)平均距離は約679 mという結果になりました。 全員が最も近い小学校に通うことで、平均通学距離をおよそ6.8%短縮できる可能性がある、という結果になりました。
ボロノイ領域による距離分布をヒストグラムにしてみます。
# 通学距離のヒストグラム
ggplot(grid_pop) + aes(x = voronoi_distance, weight = student) +
geom_histogram(boundary = 0, binwidth = 200,
color = 'red', fill = "white") +
geom_vline(xintercept = mean_dist_voronoi,
color = "red", linetype = "dashed") +
theme_minimal()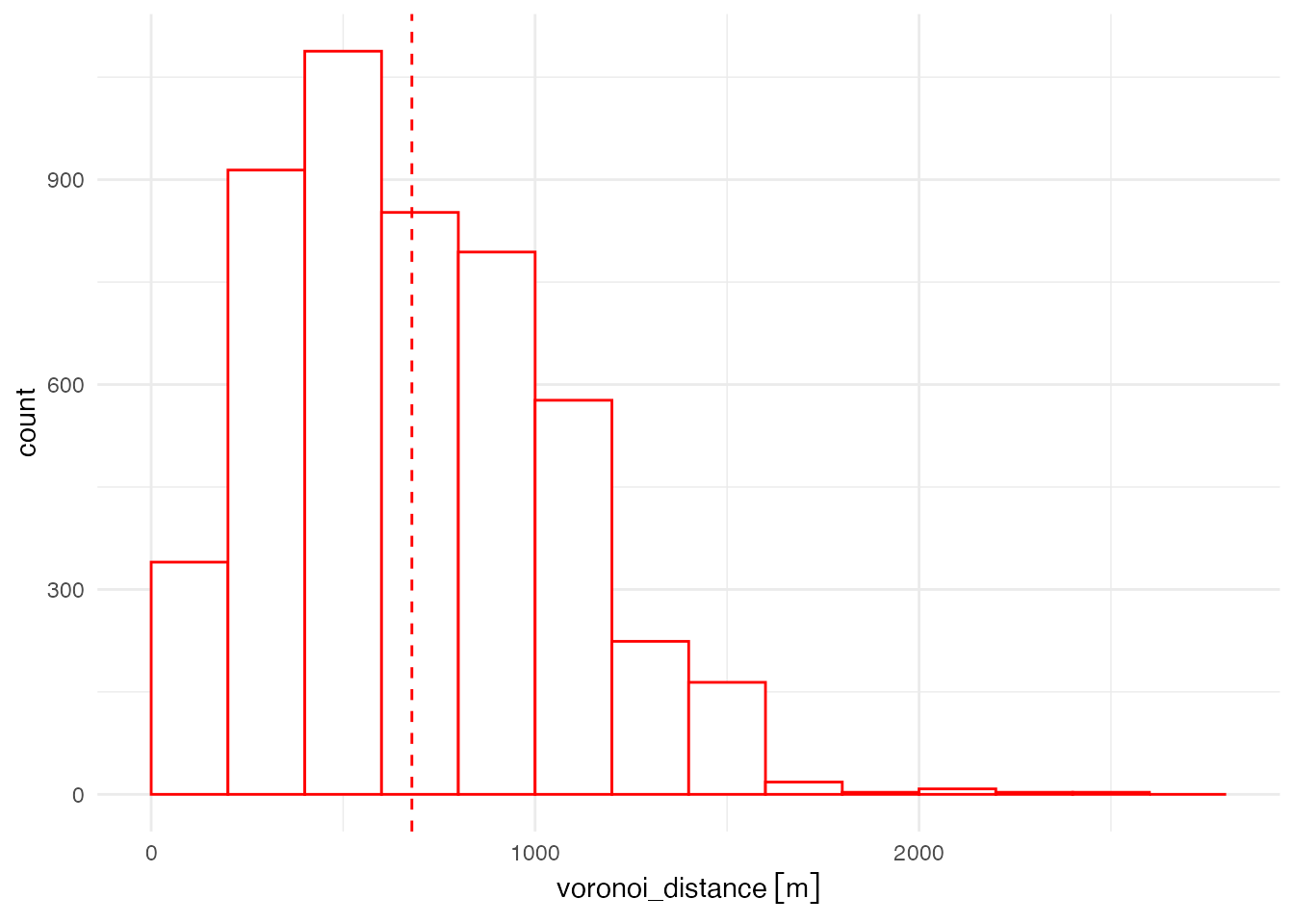
小学校区による距離分布と重ねて表示すると、こんな感じになります。
# ヒストグラムの重ね合わせ
ggplot(grid_pop) + aes(weight = student) +
geom_histogram(aes(x = school_distance),
boundary = 0, binwidth = 200,
color = grey(0.2), fill = grey(0.8),) +
geom_vline(xintercept = mean_dist_school, linetype = "dashed") +
geom_histogram(aes(x = voronoi_distance), alpha = 0.5,
boundary = 0, binwidth = 200,
color = 'red', fill = NA) +
geom_vline(xintercept = mean_dist_voronoi,
color = "red", linetype = "dashed") +
theme_minimal()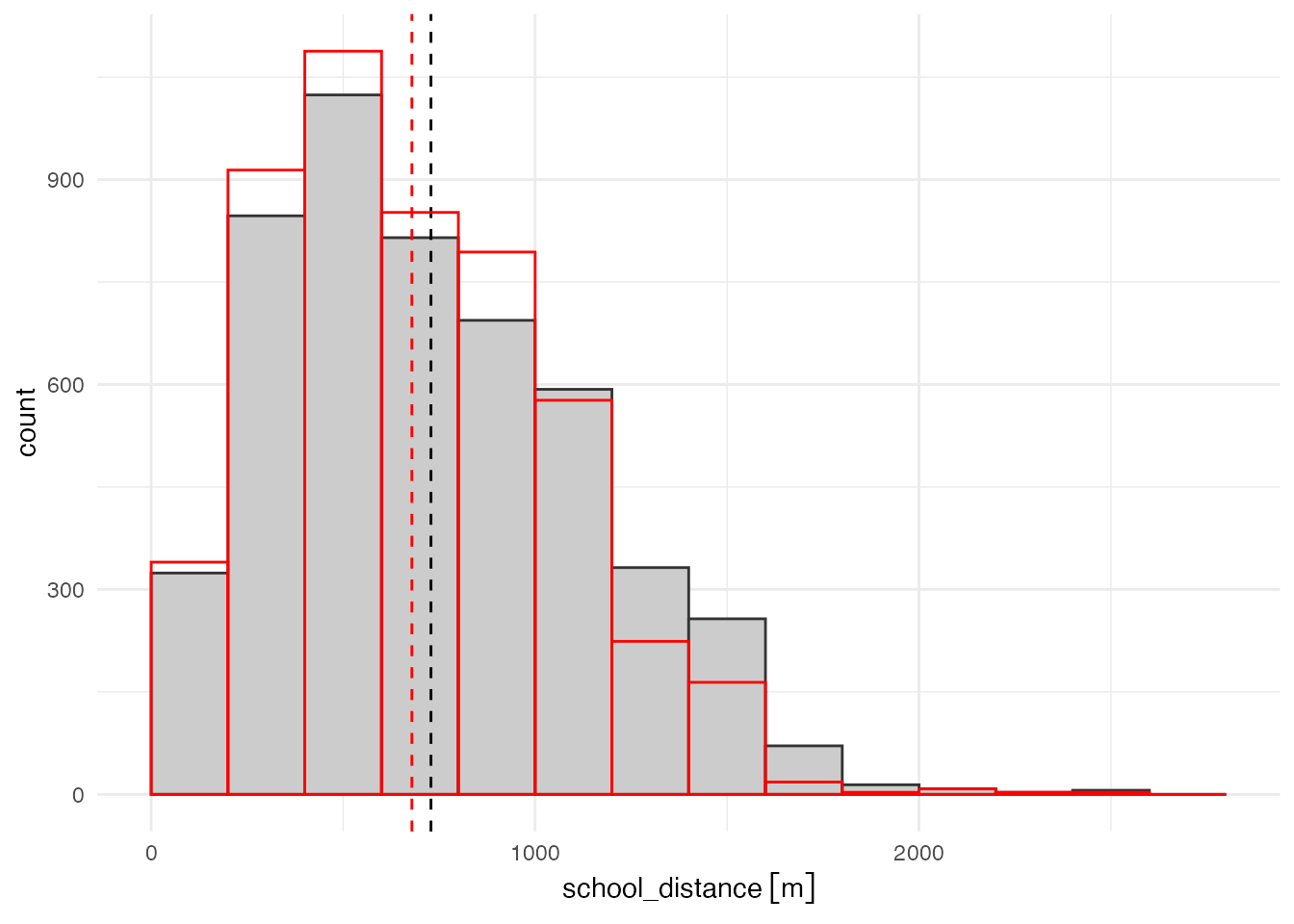
小学校からの距離が1,200〜1,800 mの人が減って、 200〜600 m、800〜1,000 mの人が増えている様子が確認できます。
累積距離分布も比較しておきましょう。
# 累積距離分布の重ね合わせ
voronoi_distance <- grid_pop |>
arrange(voronoi_distance) |>
mutate(count = cumsum(student))
ggplot() + aes(y = count / sum(student)) +
geom_line(aes(x = school_distance), data = school_distance) +
geom_vline(xintercept = mean_dist_school, linetype = "dashed") +
geom_line(aes(x = voronoi_distance), data = voronoi_distance, color = 'red') +
geom_vline(xintercept = mean_dist_voronoi,
color = "red", linetype = "dashed") +
scale_y_continuous(name = "cumulative ratio", labels = scales::percent) +
theme_minimal()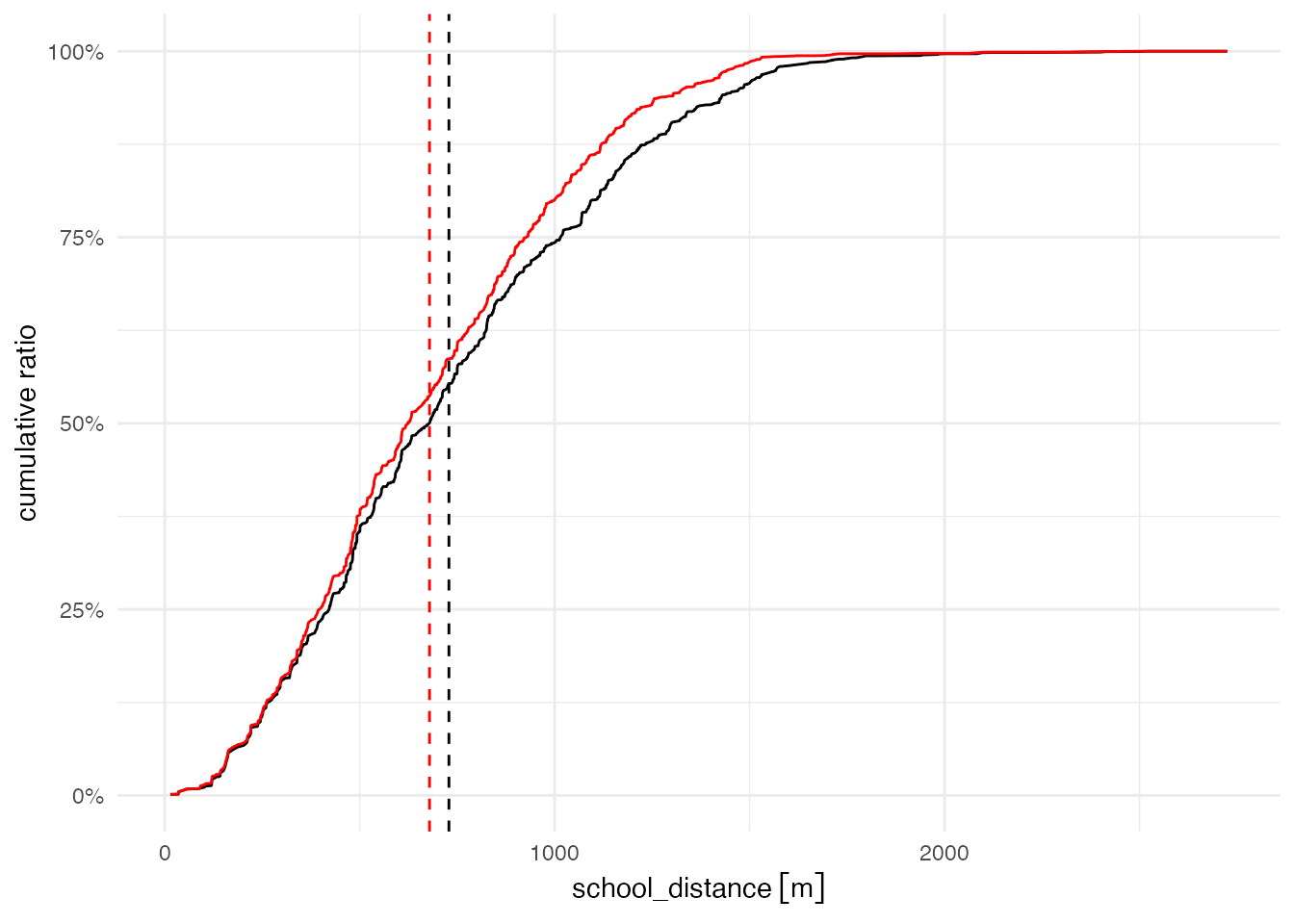
実際の小学校区による累積距離分布のほうが、ボロノイ図による分布よりも少し右側、すなわち距離が長い方向にシフトしていることがわかります。 ボロノイ図による通学距離というのは、全ての生徒が一番近い学校に通っている状態ですから、これ以上通学距離を短くすることはできません。 したがって、現状の人口分布と学校の立地を所与としたときには、どのような校区を考えても、赤い線よりも左に累積分布の線が引かれることはありません。
実際の校区設定は、通学距離だけでなく、さまざまな要素を考慮して決定されているものと思われます。 例えば、児童を受け入れる側の小学校のキャパシティもその1つでしょう。 仮に、小学校区をボロノイ領域に一致するように設定した場合、 各学校の児童数はどのようになるかを計算しておくことには意味があると思います。
# 各学校の通学人数
voronoi_pop <- grid_pop |>
group_by(voronoi_school) |>
summarise(voronoi_student = sum(student, na.rm = TRUE) * (2/3)) |>
right_join(reog_data, by = join_by(voronoi_school == school))現在の小学校の児童数と、学区を変更した場合の推計児童数を散布図にしてみます。
# 児童数の散布図(現在の校区とボロノイ図の比較)
ggplot(voronoi_pop) +
geom_point(aes(x = student, y = voronoi_student)) +
geom_abline(slope = 1, intercept = 0, color = 'red') +
theme_minimal()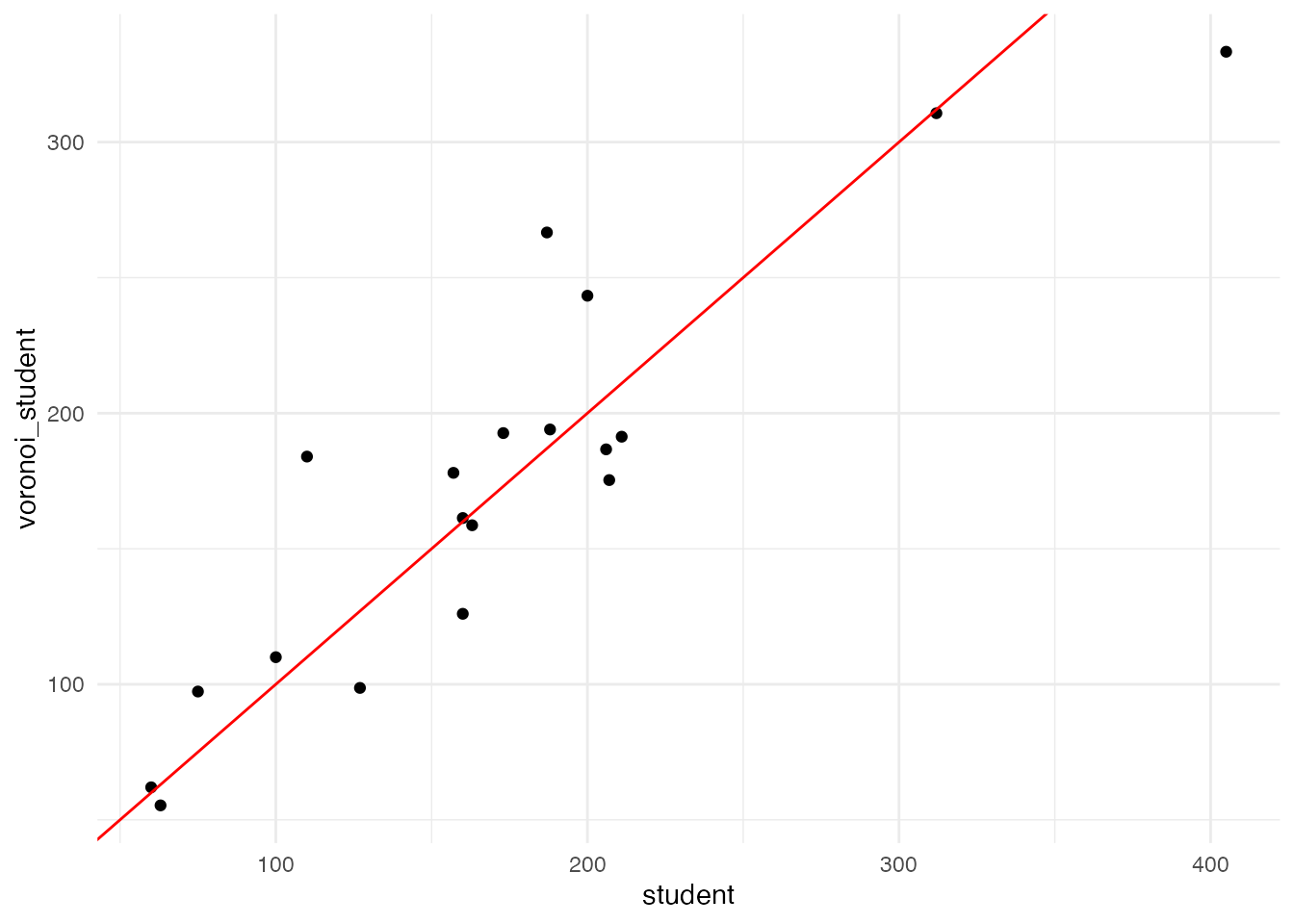
45度線上に点があれば、児童数の変化がない、ということです。 しかし図を見ると、学校あたり数十人程度の増減があり、その影響は小さくないようです。
統廃合の影響評価
柳川市の小中学校再編計画では、 現在19校ある小学校を、5校の小学校そして2校の義務教育学校(小中一貫校)に再編する計画になっています。 現在19校ある学校を、7校に減らすわけですから、その影響とても大きいことが予想されます。 では、どのくらいの影響があるのか、通学距離に絞って、定量的に見積もってみましょう。
将来の小学校区の可視化
再編後の小学校区は、現在の小学校区の組み合わせで構成されています。 ですので、現在の小学校区のデータを組み合わせて、将来の校区のデータを作ることが可能です。
まず、現在の校区データ(district)に、学校再編の情報(reog_data)を結合します。 結合にはdplyr::left_join関数を使います。結合のキーには学校名称を使うので、 dplyr::join_by関数でそれぞれのデータフレームにおいて学校名が入っている列名を指定しています。
結合したデータにある、将来の小学校名を使って、校区データを(空間的に)集計します。 dplyr::group_by関数を使って、新しい学校名でグルーピングしたあと、dplyr::summarise関数で集計します。
# 将来の小学校区
future_district <- district |>
left_join(reog_data, by = join_by(school)) |>
group_by(future_school) |> summarise()将来の小学校の位置データも作成しましょう。 柳川市の小中学校再編計画では、将来の小中学校の位置は、現在ある小中学校の敷地を活用することになっています。
将来の小学校について、現在のどの学校の敷地を利用するかを表に整理したものを、 先ほどダウンロードしたExcelファイルの2つ目のシート(シート名:location)にしてありますので、これを読み込んで利用しましょう。
# 将来の小学校の場所(現在の小中学校の敷地)
school_site <-
read_excel("data/yanagawa_es_reog.xlsx", sheet = "location")locationの内容は、以下のようになっています。
| future_school | school |
|---|---|
| 柳城小学校 | 城内小学校 |
| 柳南小学校 | 柳南中学校 |
| 昭代学校 | 昭代第二小学校 |
| 蒲池学校 | 蒲池小学校 |
| 大和小学校 | 大和中学校 |
| 藤吉小学校 | 藤吉小学校 |
| 三橋小学校 | 三橋中学校 |
これは、例えば、新しい「柳城小学校」は、現在の「城内小学校」の敷地を利用することを意味しています。 これを使って、国土数値情報の学校データから、柳川市の将来の小学校(ポイント)データを作成しましょう。
# 将来の小学校ポイントデータ
future_location <-
st_read("data/P29-23_40_GML/P29-23_40.geojson") |>
mutate(school = str_remove(P29_004, "^柳川市立")) |>
filter(P29_001 == "40207", school %in% school_site$school) |>
left_join(school_site, by = join_by(school)) |>
select(future_school) |> st_transform(6670)Reading layer `P29-23_40' from data source
`/Users/kzktmr/Documents/LectureNotes/EconomicGeography/data/P29-23_40_GML/P29-23_40.geojson'
using driver `GeoJSON'
Simple feature collection with 2027 features and 9 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 130.0358 ymin: 33.0043 xmax: 131.1882 ymax: 33.99282
Geodetic CRS: JGD20111行目は、sf::st_read関数で学校のGeoJSONファイルを読み込んでいます。 3行目は、filter関数を使って、柳川市の学校のうち、将来の小学校敷地として利用される学校 のデータだけを抜き出しています。 5行目は、left_join関数を使って、現在の学校名称(school)をキーにして、将来の学校名称を結合しています。 6行目は、select関数を使って、将来の学校名称(と位置情報)だけのポイントデータにしています。
作成した将来の小学校区と将来の小学校の位置を、地図に重ねて表示します。 19あった小学校が7校に減るわけですから当然なのですが、校区の規模がかなり大きくなっています。
# 将来の小学校区(地図)
ggplot() +
geom_sf(data = future_district) +
geom_sf(data = future_location) +
theme_minimal()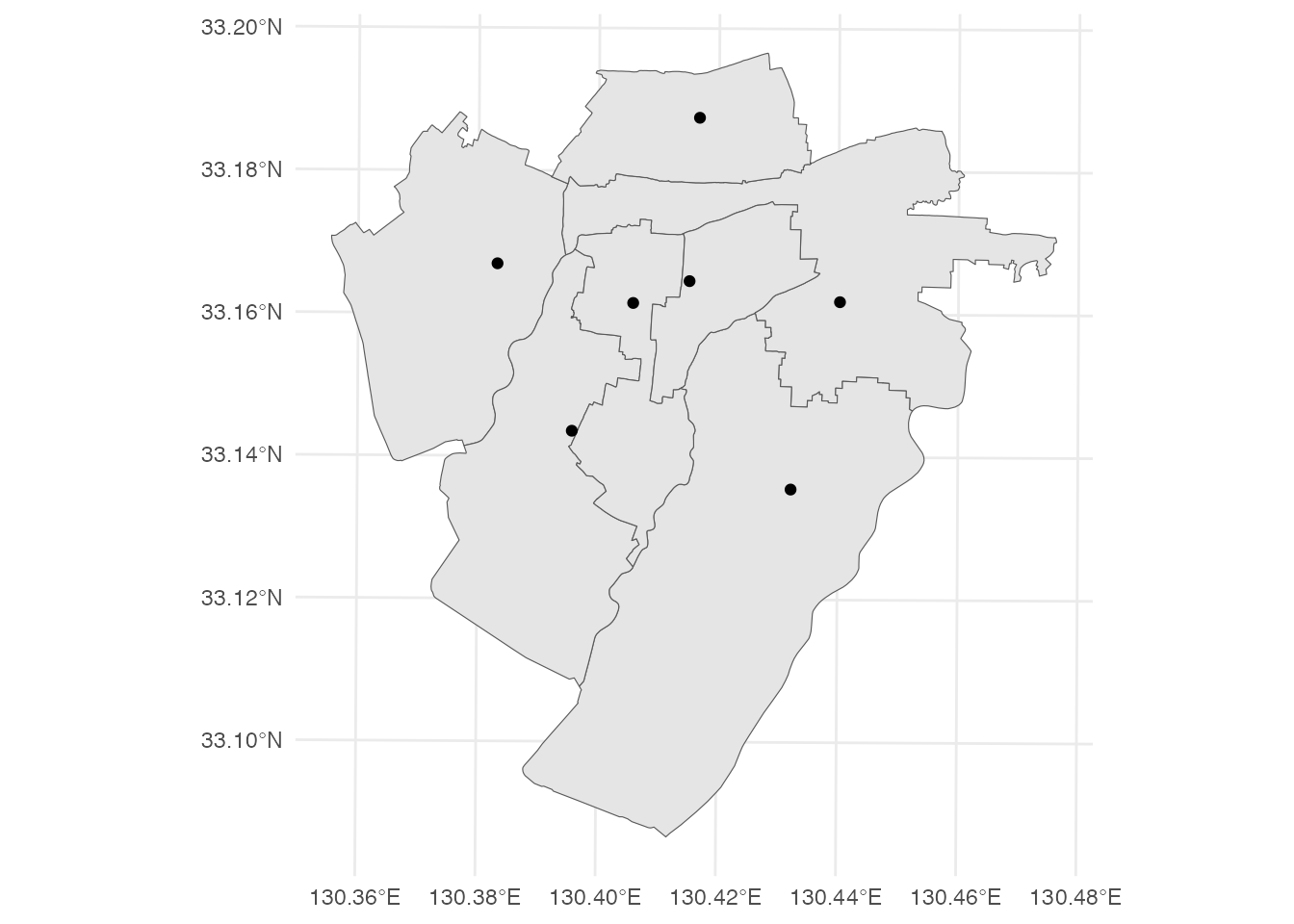
通学距離の変化を見積もる
将来の小学校区のデータを使って、小学校の再編が通学距離に与える影響を見積もってみましょう。
作業内容としては、現在の小学校区の学校までの距離を測る作業と全く同じ方法を使って、 将来の小学校区における学校までの距離を計測します。 そして、現在と将来の通学距離の分布を比較する、という手順になります。
# 将来の小学校ポイントデータを加工
future_location <- future_location |>
mutate(future_geometry = st_geometry(future_location)) |>
st_drop_geometry()
glimpse(future_location)Rows: 7
Columns: 2
$ future_school <chr> "柳城小学校", "昭代学校", "藤吉小学校", "柳南小学校", "三橋小学校", "蒲池学校", "大…
$ future_geometry <POINT [m]> POINT (-55422.91 18064.95), POINT (-57530.71 186…各メッシュから、将来の校区の小学校までの距離を計測します。
# 将来の通学距離を計算
grid_pop <- grid_pop |>
st_join(future_district) |>
left_join(future_location, by = join_by(future_school)) |>
mutate(future_distance = st_distance(geometry, future_geometry, by_element = TRUE))
glimpse(grid_pop)Rows: 723
Columns: 13
$ grid <grd250> 4930531223, 4930531333, 4930532311, 4930532324, 49…
$ geometry <POINT [m]> POINT (-55277.44 10667.83), POINT (-54691.45 11…
$ meshcode <chr> "4930531223", "4930531333", "4930532311", "4930532324…
$ student <dbl> 0, 7, 0, 0, 3, 0, 3, 3, 0, 0, 3, 0, 1, 0, 0, 2, 6, 9,…
$ school <chr> "有明小学校", "有明小学校", "有明小学校", "中島小学校", "有明小学校", "有明小学校",…
$ school_geometry <POINT [m]> POINT (-54174.45 13159.02), POINT (-54174.45 13…
$ school_distance [m] 2724.4535 [m], 2097.1239 [m], 1873.7285 [m], 2398.4239 …
$ voronoi_school <chr> "有明小学校", "有明小学校", "有明小学校", "有明小学校", "有明小学校", "有明小学校",…
$ voronoi_geometry <POINT [m]> POINT (-54174.45 13159.02), POINT (-54174.45 13…
$ voronoi_distance [m] 2724.4535 [m], 2097.1239 [m], 1873.7285 [m], 1615.9226 …
$ future_school <chr> "大和小学校", "大和小学校", "大和小学校", "大和小学校", "大和小学校", "大和小学校",…
$ future_geometry <POINT [m]> POINT (-52977.66 15164.76), POINT (-52977.66 15…
$ future_distance [m] 5050.878 [m], 4386.751 [m], 4174.521 [m], 3677.238 [m],…計測した距離から、平均距離を計算しましょう。
# 将来の平均通学距離
mean_dist_future <-
weighted.mean(grid_pop$future_distance, grid_pop$student)
mean_dist_future1306.031 [m]再編後の平均通学距離はおよそ1306 mとなり、小学校の再編で平均的な通学距離は現在の約1.8倍になると見積もることができます。
距離分布のグラフを書いてみましょう。 長い距離を通学する児童が増えるので、裾が長い分布になります。
# 将来の通学距離のヒストグラム
ggplot(grid_pop) +
aes(x = future_distance, weight = student) +
geom_histogram(alpha = 0.2, boundary = 0, binwidth = 200,
color = 'blue', fill = 'blue') +
geom_vline(xintercept = mean_dist_future,
color = "blue", linetype = "dashed") +
theme_minimal()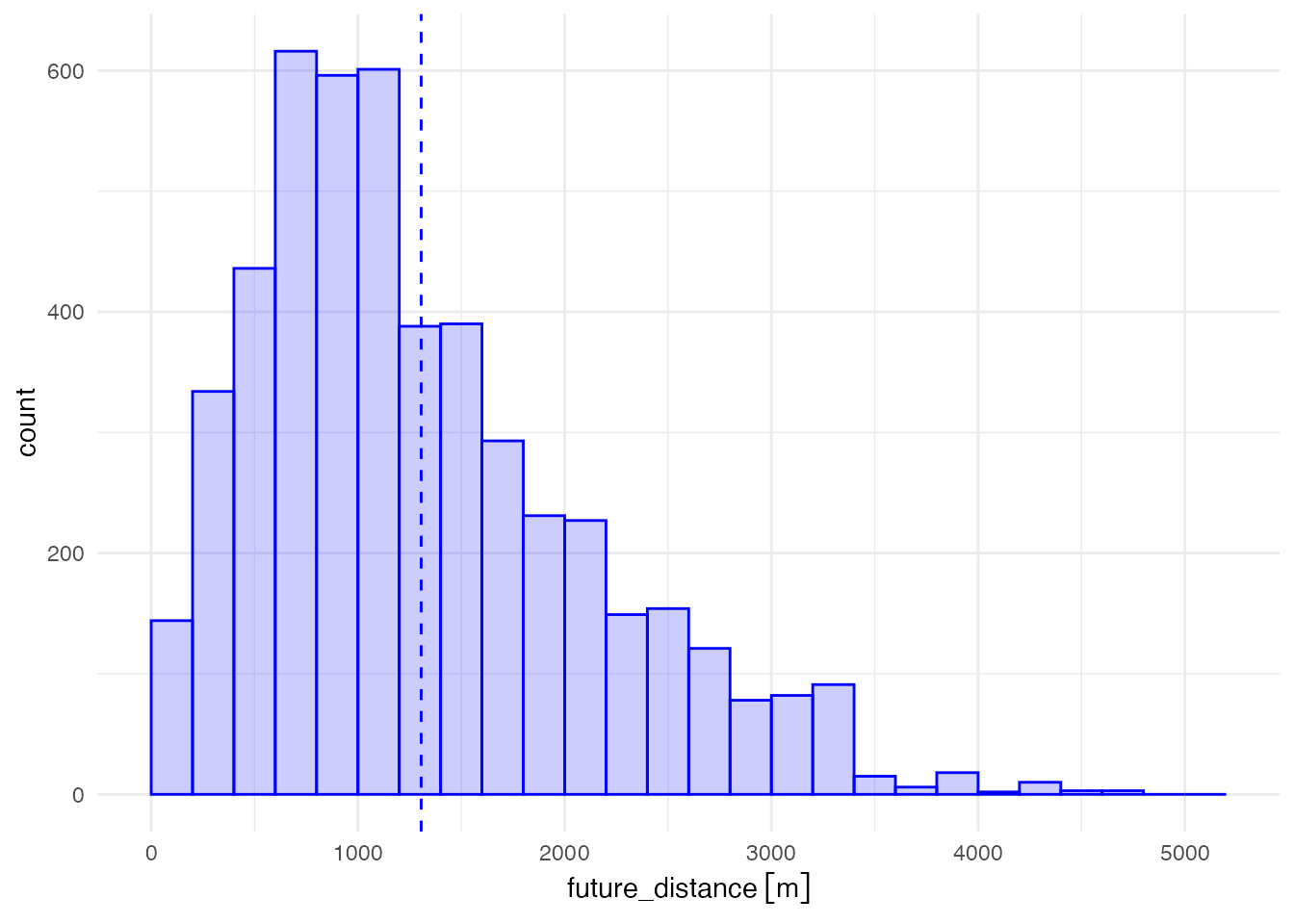
累積分布はこのようになります。 学校までの直線距離が1,000 m以下の児童は全体の40%強、2,000 mを超える児童がおよそ20%いることがわかります。 最も学校が遠い児童では、その距離は5 kmを超えます。
# 将来の通学距離の累積分布
future_distance <- grid_pop |>
arrange(future_distance) |>
mutate(count = cumsum(student))
ggplot(future_distance) +
aes(x = future_distance, y = count / sum(student)) +
geom_line(color = "blue") +
geom_vline(xintercept = mean_dist_future,
color = "blue", linetype = "dashed") +
scale_y_continuous(name = "cumulative ratio", labels = scales::percent) +
theme_minimal()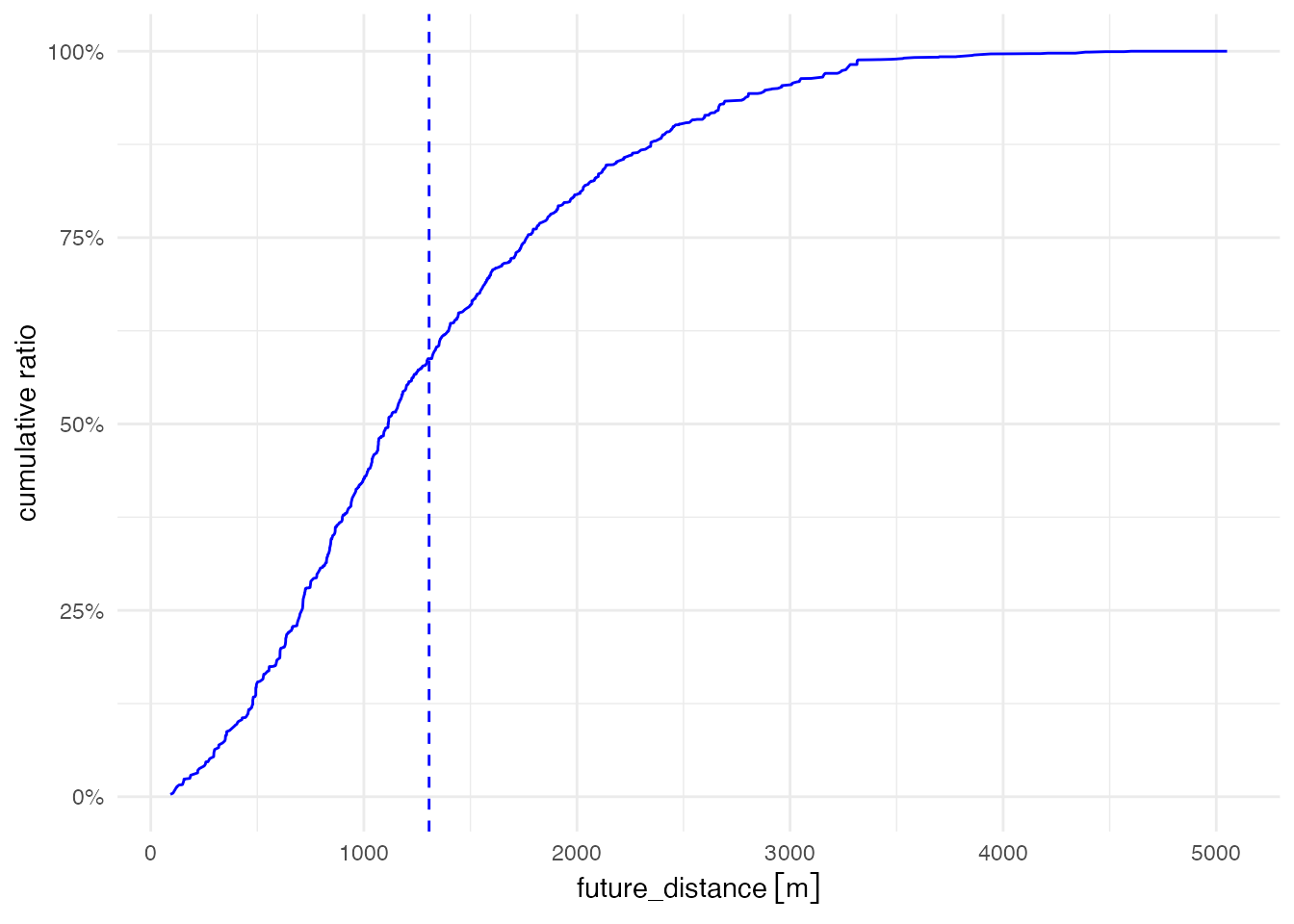
現在の学校配置における距離分布と重ねてみましょう。 グレーのグラフが現在の小学校区における距離分布、青色のグラフが将来の小学校区における距離分布です。 この図からも、小学校の統廃合によって、学校までの距離が1,000m以下の人数が大きく減り、 1,500m以上の人数が大きく増えることが確認できます。
# 現在と将来の通学距離の比較(ヒストグラム)
ggplot(grid_pop) + aes(weight = student) +
geom_histogram(aes(x = school_distance),
boundary = 0, binwidth = 200,
color = grey(0.2), fill = grey(0.8),) +
geom_vline(xintercept = mean_dist_school, linetype = "dashed") +
geom_histogram(aes(future_distance), alpha = 0.2,
boundary = 0, binwidth = 200,
color = 'blue', fill = 'blue') +
geom_vline(xintercept = mean_dist_future,
color = "blue", linetype = "dashed") +
theme_minimal()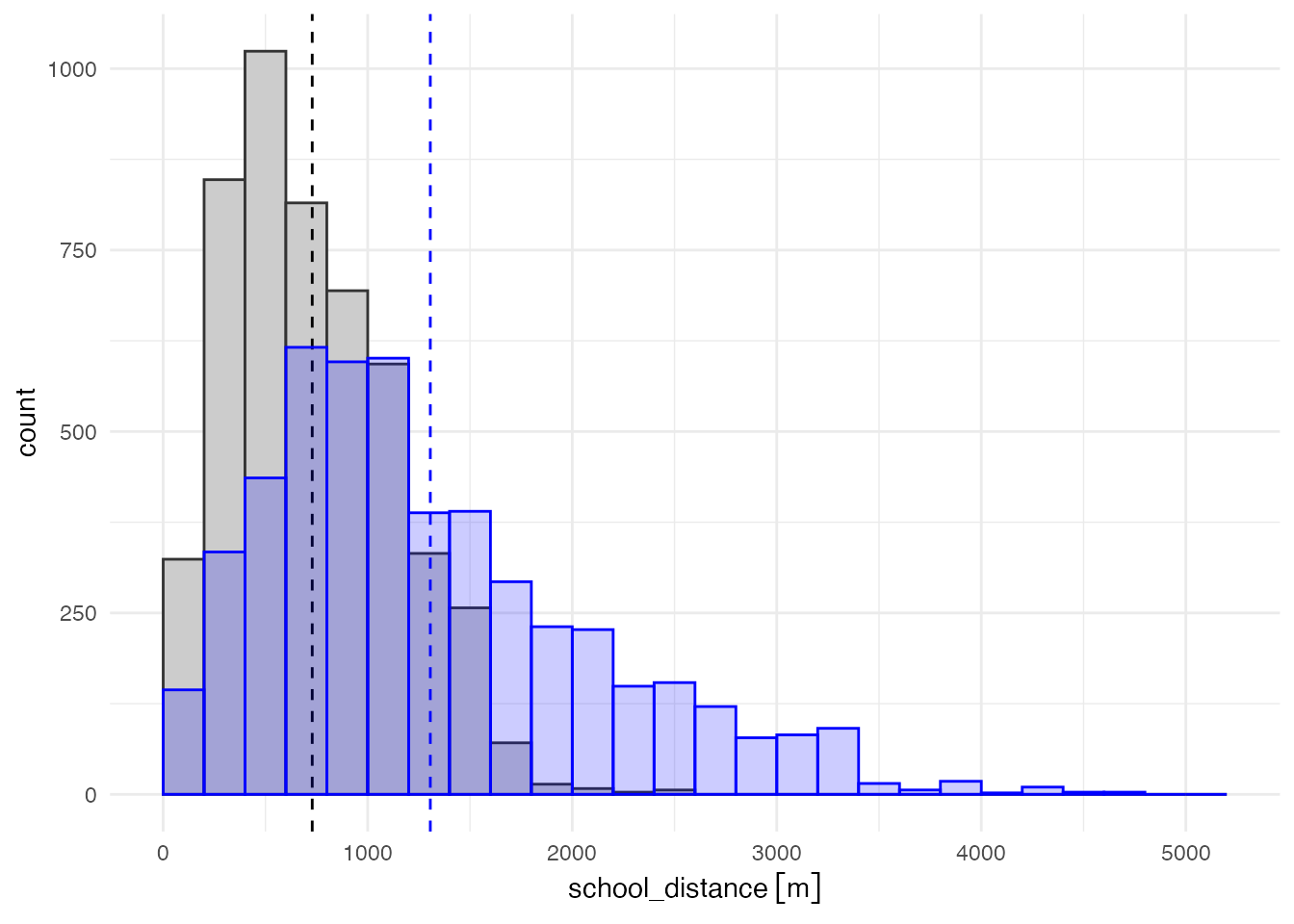
累積距離分布も比較しておきましょう。 言うまでもなく、青色の線が、将来の学校配置による分布です。 距離が伸びる方向に大きくシフトしていることがわかります。
# 現在と将来の通学距離の比較(累積分布)
ggplot() + aes(y = count / sum(student)) +
geom_line(aes(x = school_distance), data = school_distance) +
geom_line(aes(x = voronoi_distance), data = voronoi_distance, color = 'red') +
geom_line(aes(x = future_distance), data = future_distance, , color = 'blue') +
geom_vline(xintercept = mean_dist_school, linetype = "dashed") +
geom_vline(xintercept = mean_dist_voronoi, color = "red", linetype = "dashed") +
geom_vline(xintercept = mean_dist_future, color = "blue", linetype = "dashed") +
scale_y_continuous(name = "cumulative ratio", labels = scales::percent) +
theme_minimal()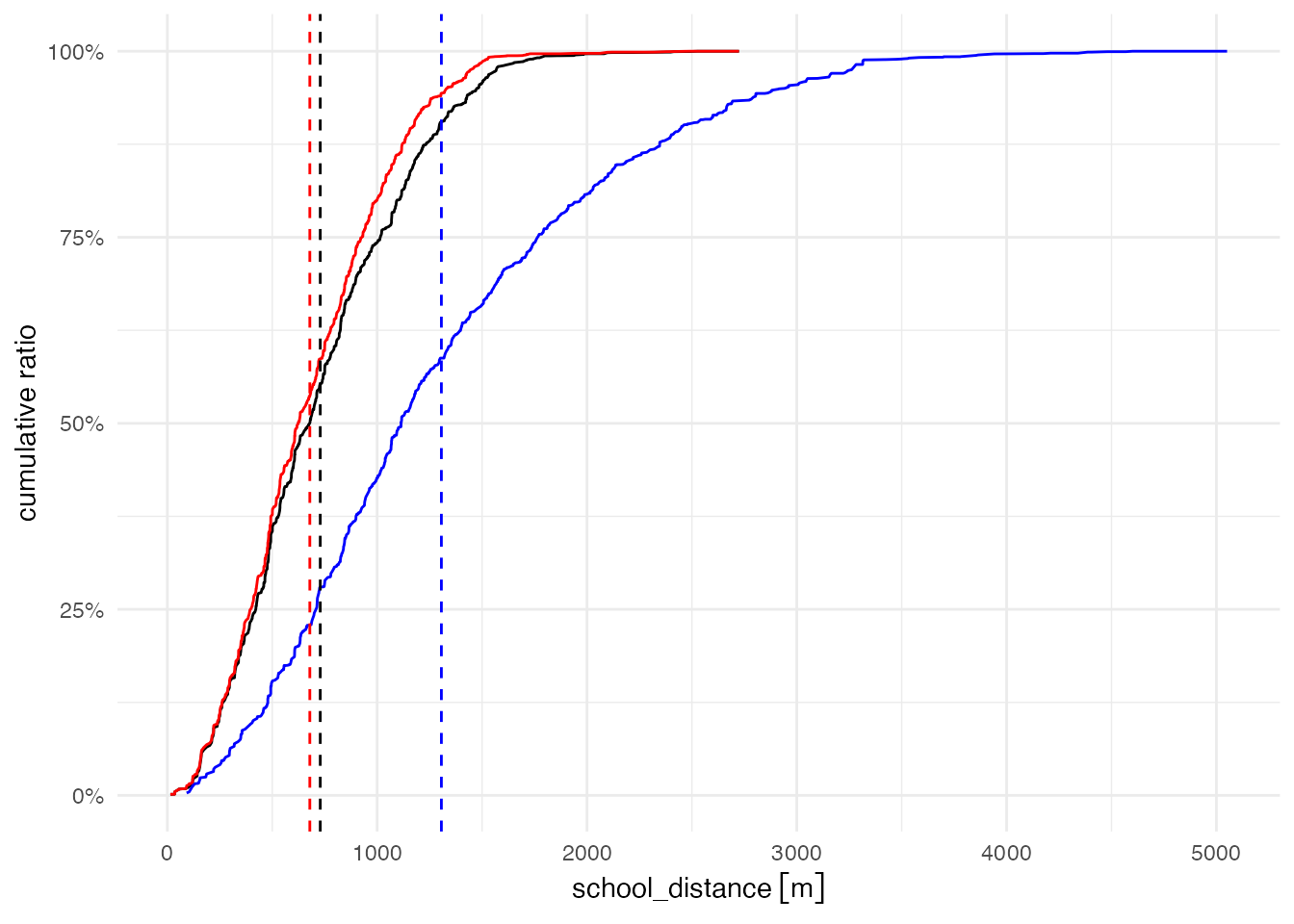
おわりに
今回の分析例では、小学校の統廃合により、学校までの平均距離が1.8倍になるという結果になりました。 このように、空間データを使って定量的な分析を行うと、政策の影響を数字で評価できるようになります。
19校を7校に減らしたということの影響だけでなく、7校の立地場所としてどこを選ぶかや、校区をどのように設定するかの影響も大きいと思います。 なお、柳川市では「通学距離が概ね2 kmを超える場合は、スクールバス等の運行を検討」するとしています2。
それぞれ政策の影響を定量的に評価するには、どのような分析を行えばよいか、ぜひ皆さんも考えてみてください。
脚注
データは 柳川市オープンデータカタログサイト:市立学校児童生徒数一覧から。↩︎
柳川市は、令和7年4月に開校した大和小学校(正式名称は「やまと小学校」)のスクールバスのために、マイクロバス(6台)購入費、スクールバス駐車場整備費、通学路安全対策費(スクールバスのルートとなる通学路の拡幅)、スクールバス運行委託費などの費用をかけています。↩︎
