library(tidyverse)
library(sf)
library(sfdep)11: 空間的自己相関
はじめに
空間的自己相関とは、簡単に言えば「近所と相関がある」という意味です。 ある地域における事象が、その周辺地域の事象に影響を受けて、互いに影響を及ぼし合っているようなとき、空間的自己相関があるといいます。
今回は、空間的な分析を行う上で重要な性質である空間的自己相関について学びましょう。
空間的自己相関とは
時系列解析における「自己相関」と同じような意味で、空間データについても自己相関という概念があります。 時系列解析においては、時々刻々と変化するデータが、それまでの(それ以前の)データとどの程度相関があるかを表す尺度として「自己相関係数」が定義されます。 空間的自己相関とは、空間的に分布するデータについて、地理的に近い地点との相関関係を持つかどうか示す指標です。 空間的自己相関は、空間相関と呼ばれることもあります。
空間相関には、近い地点どうしの値が似た傾向を持つという正の空間相関と、近所と逆の傾向をもつという負の空間相関があります。 例えば、地価の高い地域の周辺地域の地価が高い傾向にあることは、正の空間相関の一例です。 売り上げの大きな店舗の周辺の店舗は、(顧客を奪われたために)売上が小さくなる傾向にあるとき、負の空間相関があると言えるでしょう。
下の図は、空間相関を模式的に現したものです。 正の空間相関をもつ空間データは分布が滑らかに変化することが多く、 反対に負の空間相関をもつデータの場合は、凸凹した(チェッカーフラッグのような模様の)分布であることが多いです。
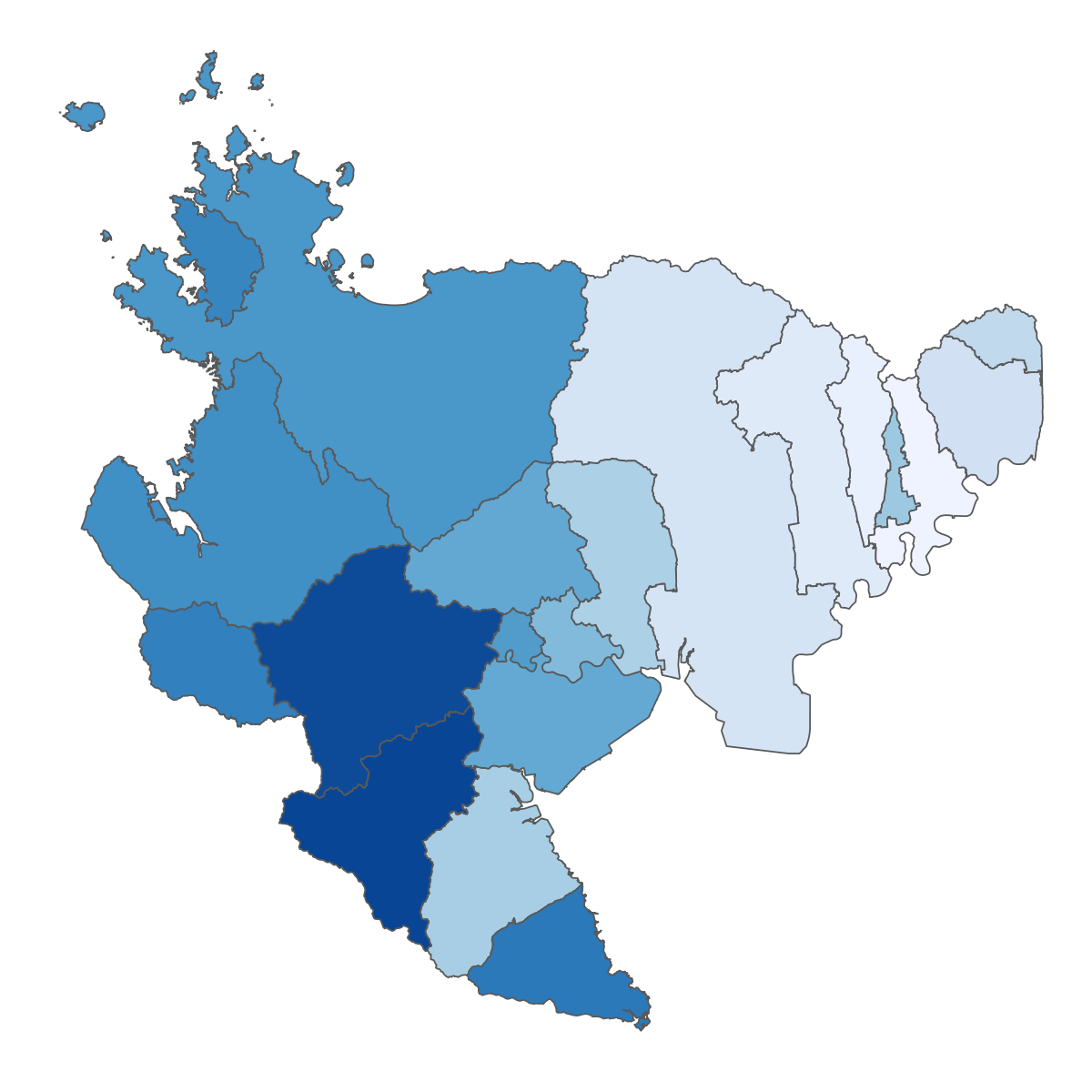
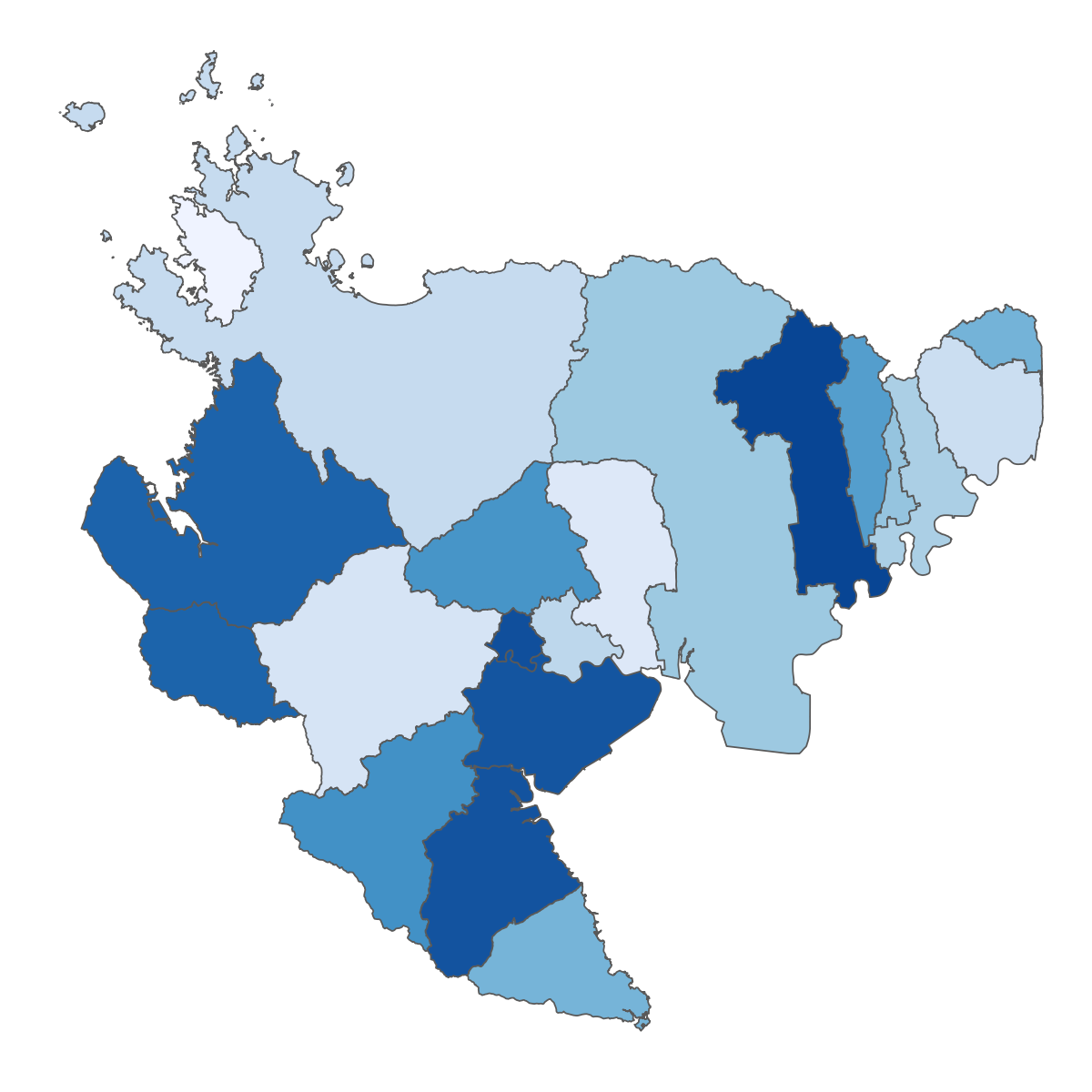
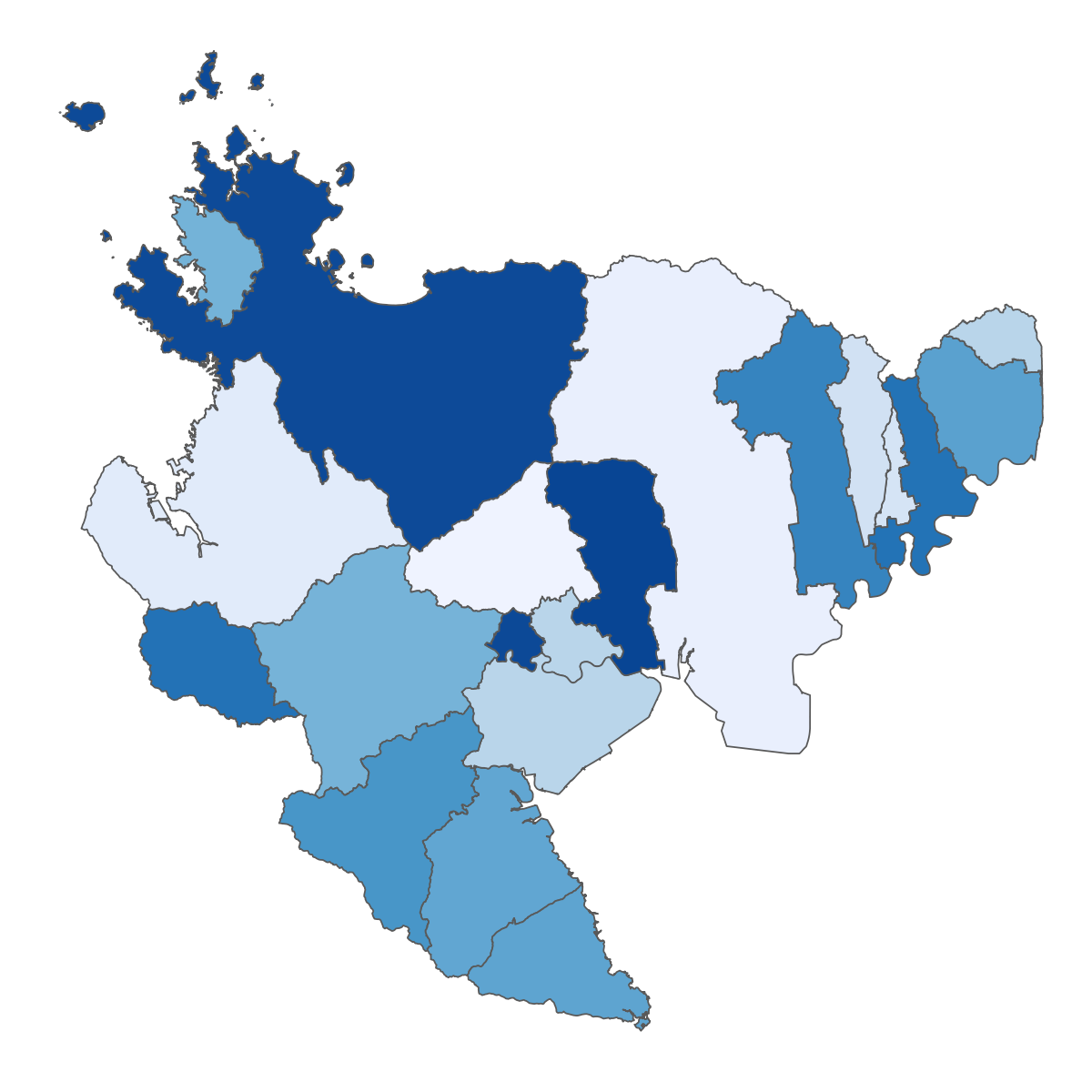
近接行列
空間的自己相関とは「近所と相関がある」ことだと言いました。 この「近所と相関がある」かどうか、つまり、地域の相互作用の有無を測るためには、「近所:neighbourhood」を定義する必要があります。 この「近所」をどう定義するかによって、空間的自己相関の分析結果も変わってきます。
具体的には、地域\(i\)と地域\(j\)が「近所である程度」の数値をその成分を\((i,j)\)要素に持つ\(N\times N\)行列(ここで\(N\)は地域の数)を考えます。 このような行列を近接行列と呼びます。
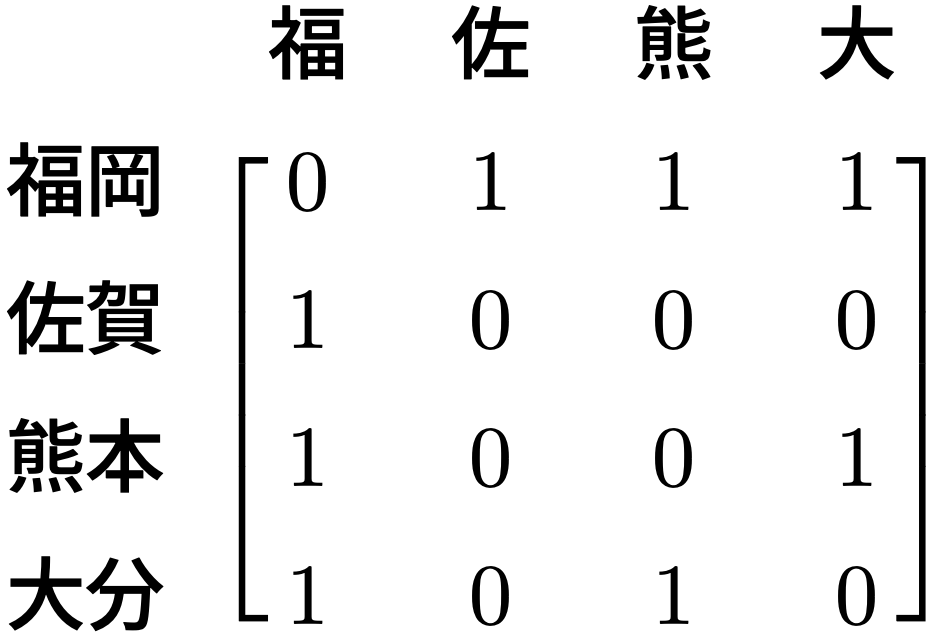
例えば、福岡、佐賀、熊本、大分の4県の「近所である程度」を考えましょう。 例としてここでは、「近所であるかどうか」を、「県境を共有しているかどうか」で定義してみます。 つまり、\(4\times 4\)の行列を考えて、2つの県がその県境を共有しているときに1、そうでないときに0となるように設定するということです。 このような近接行列を、隣接行列と呼ぶことがあります。
なお、近接行列の対角成分は0にしています。 これは、同じ地域どうしの空間的な相関関係は考慮しない、ということを意味します。
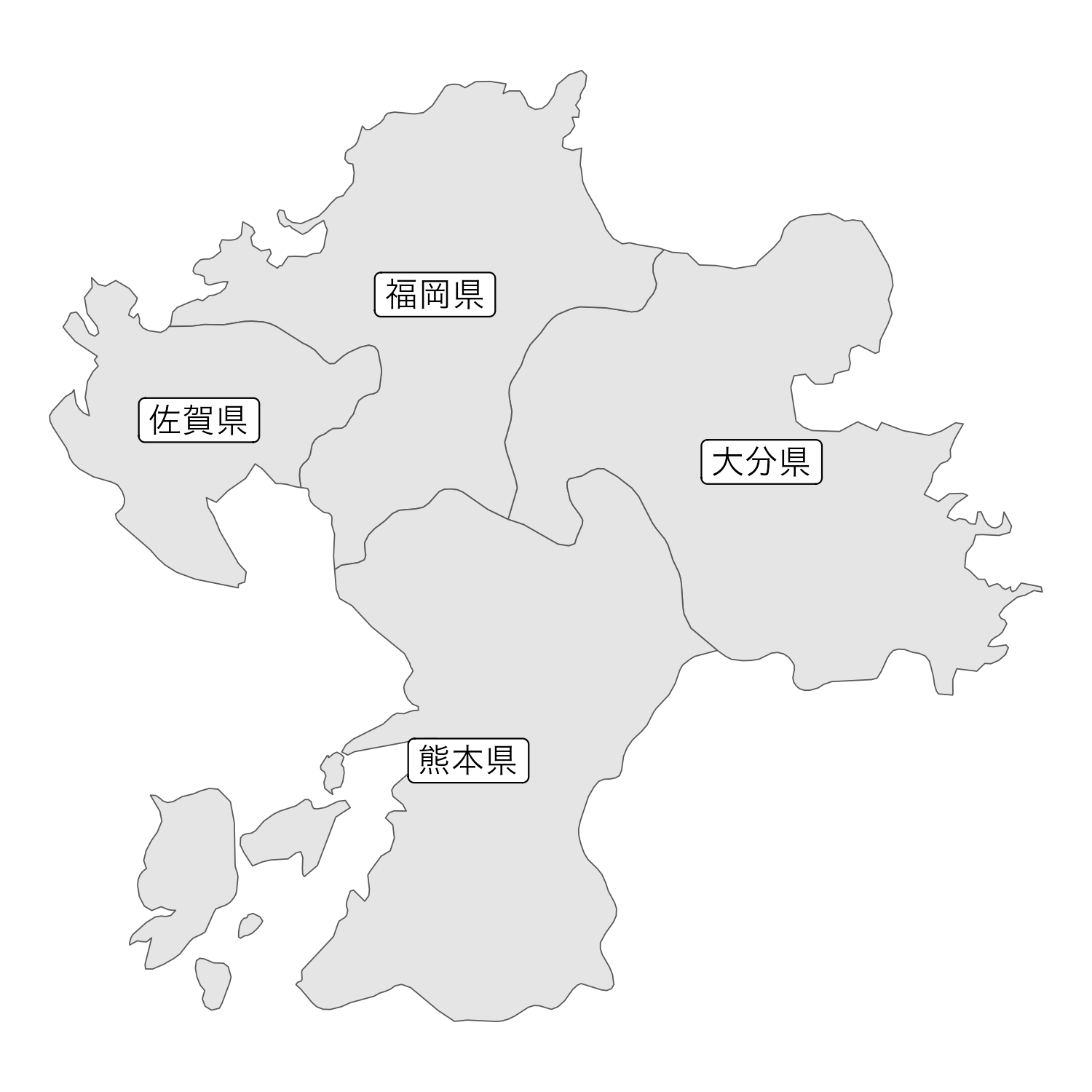
近接行列の行基準化
近接行列は、行基準化されることがあります。 行基準化とは、行列の行和が1になるように、行の要素を定数倍することです。 例えば、上の4県の隣接行列を行基準化すると、次のようになります。
\[ \left[ \begin{array}{cccc} 0 & 1/3 & 1/3 & 1/3 \\ 1 & 0 & 0 & 0 \\ 1/2 & 0 & 0 & 1/2 \\ 1/2 & 0 & 1/2 & 0 \\ \end{array}\right] \]
行基準化することで、結果を解釈しやすくなるなどのメリットがあります。
演習
準備
今日の演習では以下の3つのパッケージを使用します。
演習で使うデータは、福岡県久留米市の小学校区データです。 久留米市オープンデータカタログサイトから「小学校区のポリゴンデータ」と「15~64歳以下人口」をダウンロードしてください。
ダウンロードしたkurume-school.geojsonと402036polygon00002.csvをプロジェクトのdataフォルダに移動してください。
GeoJSONファイルをsf::st_read関数で読み込みましょう。 平面直角座標系II系に投影変換しておきます。
kurume <- st_read('data/kurume-school.geojson') |>
st_transform(6670)Reading layer `kurume-school' from data source
`/Users/kzktmr/Documents/LectureNotes/data/kurume-school.geojson'
using driver `GeoJSON'
Simple feature collection with 46 features and 1 field
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 130.3852 ymin: 33.22395 xmax: 130.7319 ymax: 33.3684
Geodetic CRS: WGS 84CSVファイルをreadr::read_csv関数を使って読み込みます。 校区ポリゴンデータと結合する際のキーとして、校区名を使いたいので、その準備をしておきます。
dat <- read_csv("data/402036polygon00002.csv") |>
select(KEY_CODE = 校区名, population = 総計)Rows: 46 Columns: 4
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): 校区名
dbl (3): 15歳~64歳以下人口(男性), 15歳~64歳以下人口(女性), 総計
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.glimpse(dat)Rows: 46
Columns: 2
$ KEY_CODE <chr> "西国分", "荘島", "日吉", "篠山", "京町", "南薫", "鳥飼", "…
$ population <dbl> 10535, 3163, 4483, 5069, 3309, 6436, 6561, 3412, 2955, 8406…校区のポリゴンデータに、読み込んだ人口データを結合(dplyr::left_join)します。
kurume <- kurume |>
left_join(dat, by = join_by(KEY_CODE))校区ポリゴンを地図にして、どのような地域なのか確認しておきましょう。
ggplot() +
geom_sf(aes(fill = population), data = kurume) +
scale_fill_distiller(direction = 1) +
theme_minimal()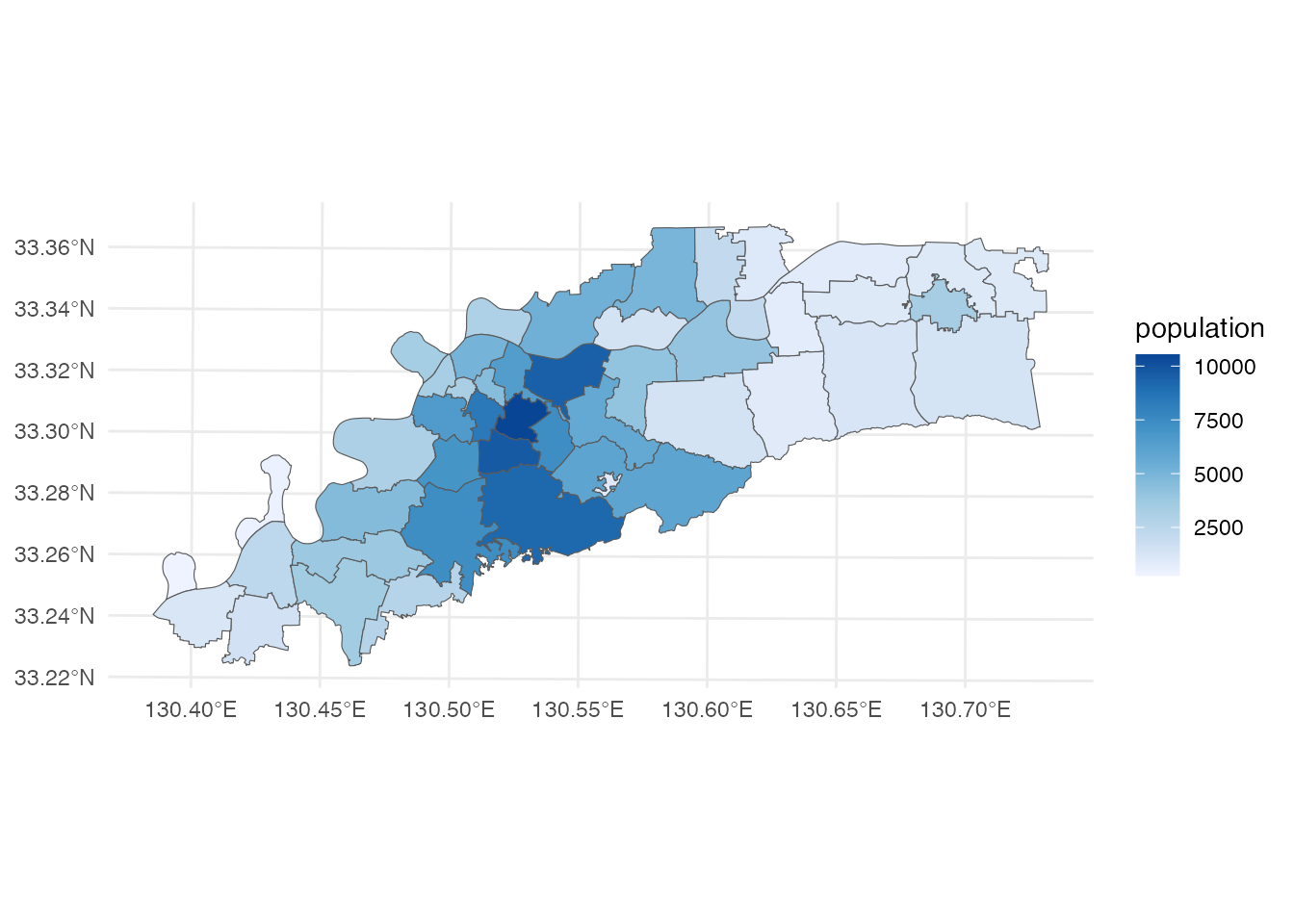
Rによる近接行列の生成
隣接
sfdep::st_contiguity関数を使うことで、簡単に隣接行列を作成することができます。
kurume_con <- kurume |>
mutate(nb = st_contiguity(geometry),
wt = st_weights(nb))
glimpse(kurume_con)Rows: 46
Columns: 5
$ KEY_CODE <chr> "上津", "城島(旧下田)", "京町", "北野", "南", "南薫", "合…
$ population <dbl> 9169, 416, 3309, 4952, 9707, 6436, 9463, 4046, 2381, 4580, …
$ geometry <MULTIPOLYGON [m]> MULTIPOLYGON (((-40259.66 3..., MULTIPOLYGON (…
$ nb <nb> <5, 22, 27, 35, 44>, 9, <32, 36, 41, 45>, <8, 11, 14, 19>, <…
$ wt <list> <0.2, 0.2, 0.2, 0.2, 0.2>, 1, <0.25, 0.25, 0.25, 0.25>, <0…nb列には、校区ごとに、その校区がどの校区と「近所」なのかというリストが格納されています。 wt列には、近接行列をsfdep::st_weights関数によって行基準化した近隣行列の要素の値(ウェイト)が格納されます。
隣接関係を地図にしてみましょう。 sfdep::st_as_graph関数を使って、sfnetworkオブジェクトを作成し、 ggplot2::autoplot関数を使って、sfnetworkオブジェクトを描画しています。
kurume_con |>
st_as_graph(nb = nb, wt = wt) |>
autoplot() + geom_sf(data = kurume, fill = NA) +
theme_minimal()Checking if spatial network structure is valid...Spatial network structure is valid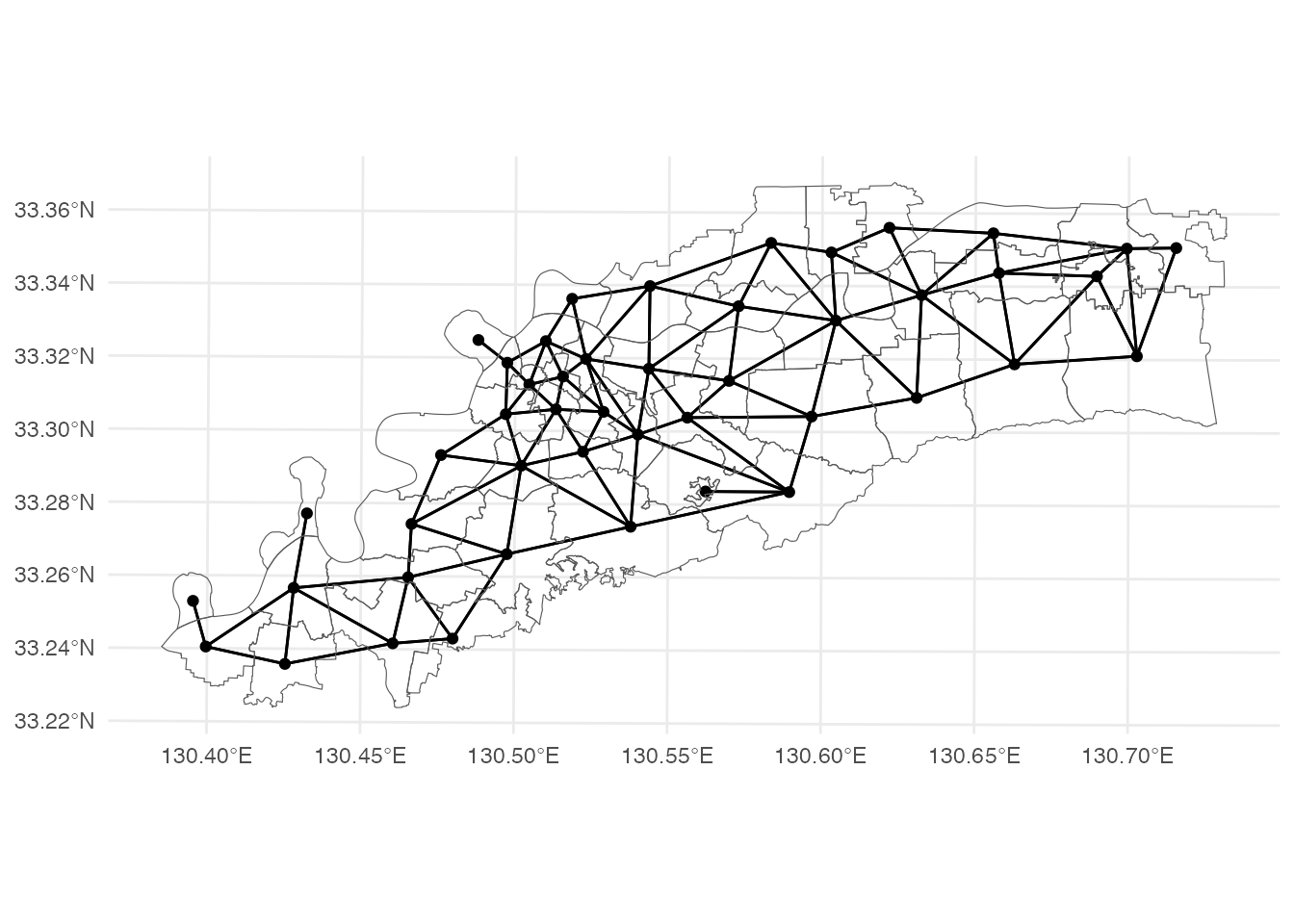
隣接関係にある校区が線で結ばれているのが確認できます。
\(k\)近隣
\(k\)近隣とは、\(k\)番目までに近い地区を「近所」だとみなすことを意味します。 Rでは、sfdep::st_knn関数を使って、\(k\)近隣行列を作成することができます。
kurume_knn <- kurume |>
mutate(nb = st_knn(geometry, k = 4),
wt = st_weights(nb))! Polygon provided. Using point on surface.glimpse(kurume_knn)Rows: 46
Columns: 5
$ KEY_CODE <chr> "上津", "城島(旧下田)", "京町", "北野", "南", "南薫", "合…
$ population <dbl> 9169, 416, 3309, 4952, 9707, 6436, 9463, 4046, 2381, 4580, …
$ geometry <MULTIPOLYGON [m]> MULTIPOLYGON (((-40259.66 3..., MULTIPOLYGON (…
$ nb <nb> <5, 22, 37, 42>, <9, 10, 28, 46>, <32, 36, 41, 45>, <8, 11, …
$ wt <list> <0.25, 0.25, 0.25, 0.25>, <0.25, 0.25, 0.25, 0.25>, <0.25,…ここでは、\(k=4\)を設定して、\(4\)近隣行列を作成しています。 ggplotで可視化してみましょう。
kurume_knn |>
st_as_graph(nb = nb, wt = wt) |>
autoplot() + geom_sf(data = kurume, fill = NA) +
theme_minimal()Checking if spatial network structure is valid...Spatial network structure is valid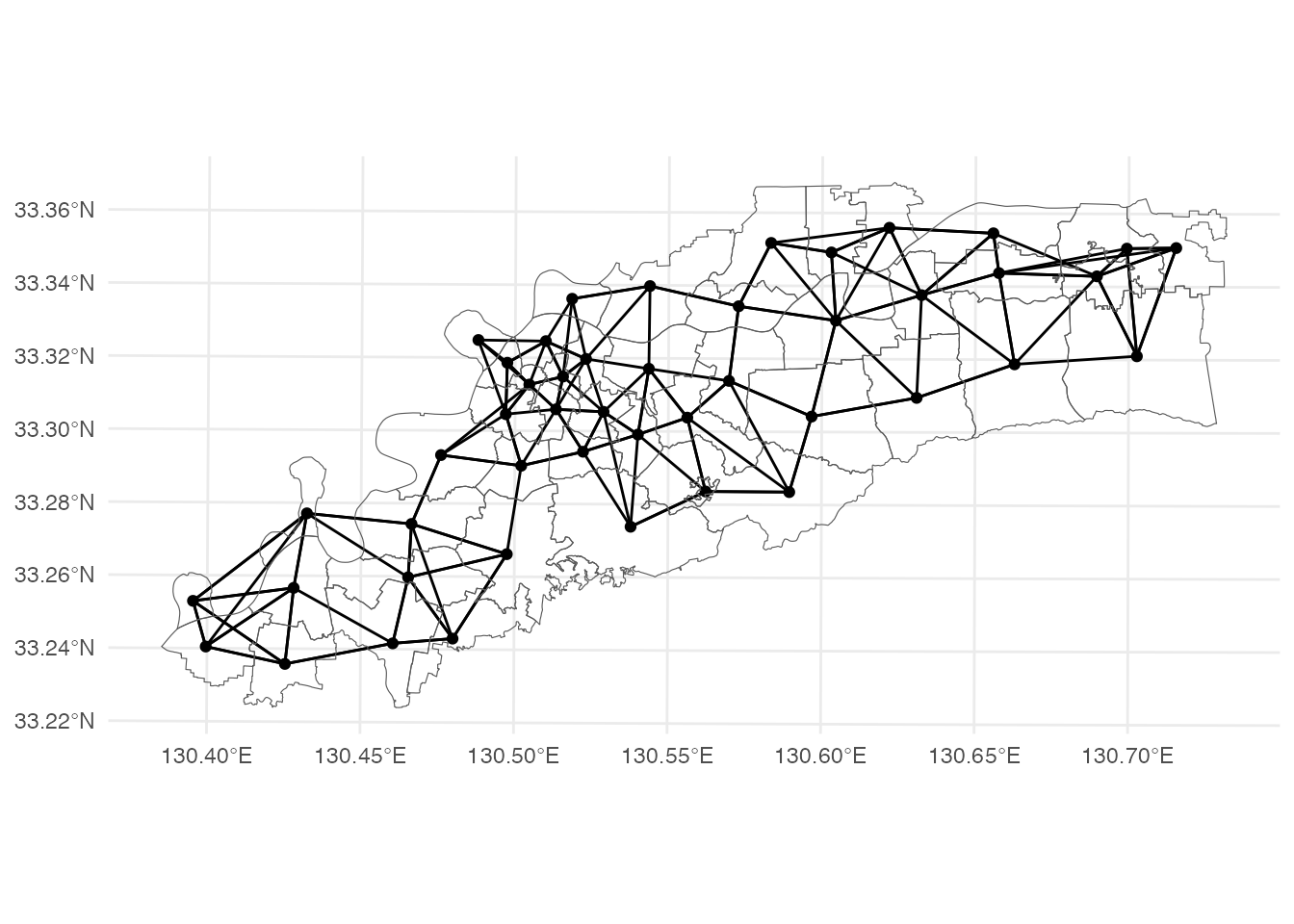
すべての点から、4本ずつ枝が伸びているのが分かります。
\(k=8\)の\(k\)近隣行列を描いてみましょう。 \(k=4\)の場合に比べ、遠くの校区が「近所」として選ばれていることが分かります。
kurume |>
mutate(nb = st_knn(geometry, k = 8),
wt = st_weights(nb)) |>
st_as_graph(nb = nb, wt = wt) |>
autoplot() + geom_sf(data = kurume, fill = NA) +
theme_minimal()! Polygon provided. Using point on surface.Checking if spatial network structure is valid...Spatial network structure is valid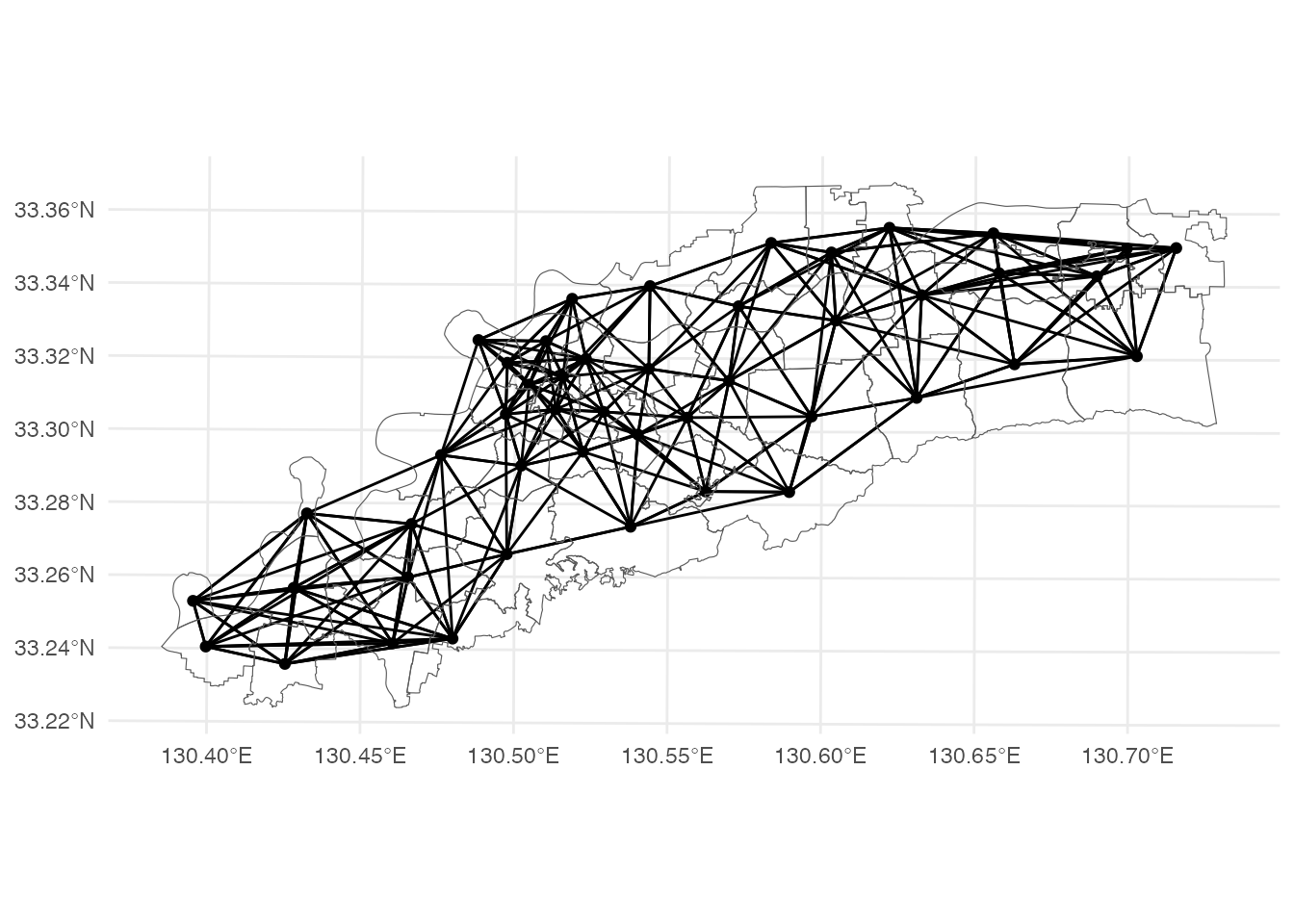
距離
地区間の距離によって「近所」かどうかを設定することもできます。 sfdep::st_dist_band関数を使います。
kurume_dst <- kurume |>
mutate(nb = st_dist_band(geometry),
wt = st_weights(nb))! Polygon provided. Using point on surface.glimpse(kurume_dst)Rows: 46
Columns: 5
$ KEY_CODE <chr> "上津", "城島(旧下田)", "京町", "北野", "南", "南薫", "合…
$ population <dbl> 9169, 416, 3309, 4952, 9707, 6436, 9463, 4046, 2381, 4580, …
$ geometry <MULTIPOLYGON [m]> MULTIPOLYGON (((-40259.66 3..., MULTIPOLYGON (…
$ nb <nb> <5, 22, 42>, 9, <6, 15, 21, 32, 36, 39, 41, 45>, <8, 11, 19>…
$ wt <list> <0.3333333, 0.3333333, 0.3333333>, 1, <0.125, 0.125, 0.125…どのような校区が「近所」となっているか、地図で確認してみます。
kurume_dst |>
st_as_graph(nb = nb, wt = wt) |>
autoplot() + geom_sf(data = kurume, fill = NA) +
theme_minimal()Checking if spatial network structure is valid...Spatial network structure is valid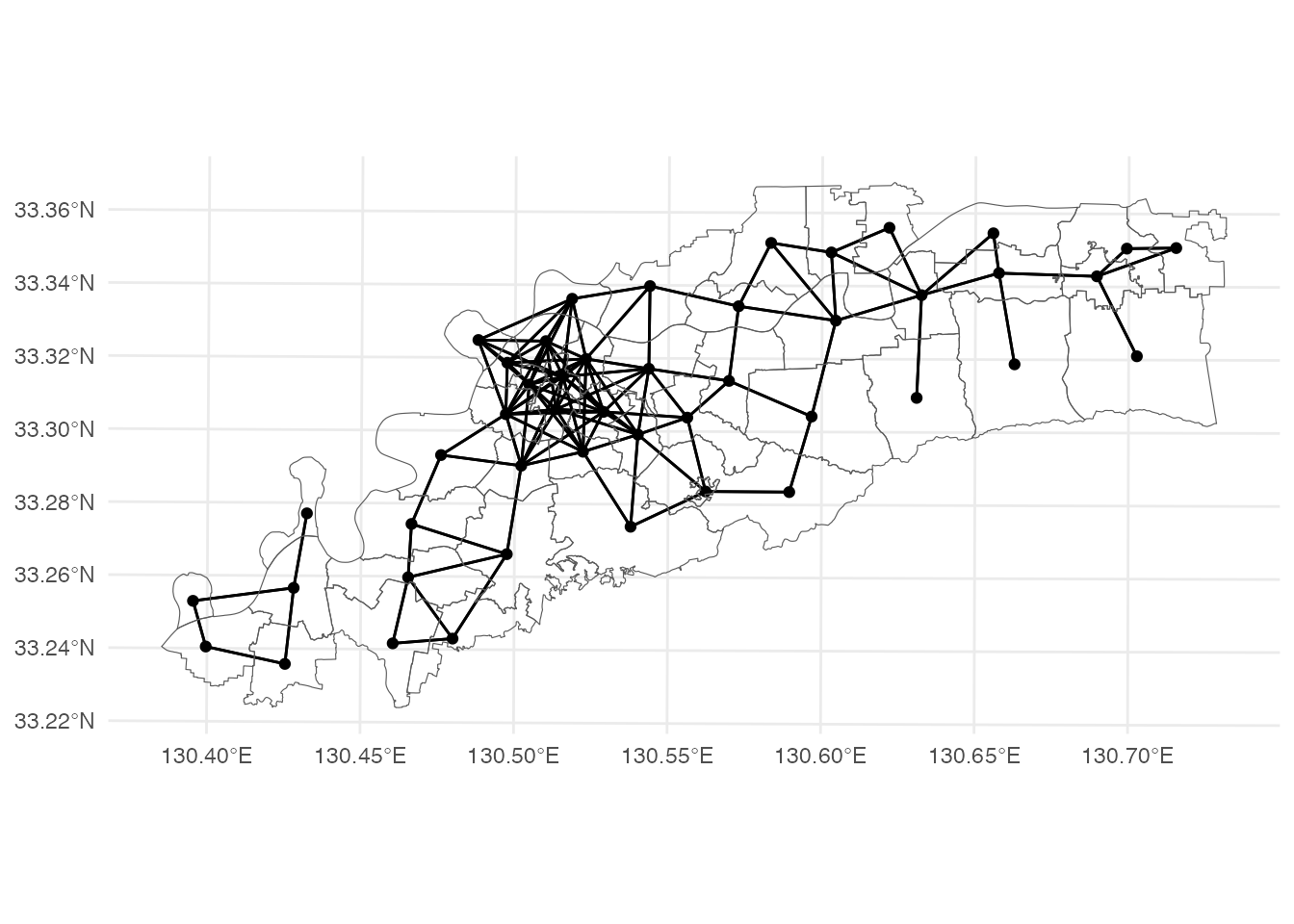
このように、距離に基づいて近接行列を作成する場合、2つ以上のグループに分割されてしまうことがあります。
sfdep::st_dist_band関数には、lowerとupperという引数があるのですが、これがどのくらいの距離帯にある地区を「近所」とみなすかの上下限値になっています。 関数の引数として上下限値を指定しない場合、lower = 0が設定され、upperについてはどの地区も1つ以上の「近所」を持つような最小の値が自動的に計算・設定されます。
この例のように、近隣行列が2つのグループに分割される場合、分断された地区の間には空間的な相関関係がない、ということを意味してしまいますから、分析の目的によっては、この手法で構成された近接行列は適当ではない、ということになるかもしれません。 その場合は、他の方法で近接行列を構成する必要があります。
あるいは、upperとして、「近所」とみなす距離の上限を上げることもできます。 例えば、upper = 4000とすると、以下のような近接行列が得られます。
kurume |>
mutate(nb = st_dist_band(geometry, upper = 4000),
wt = st_weights(nb)) |>
st_as_graph(nb = nb, wt = wt) |>
autoplot() + geom_sf(data = kurume, fill = NA) +
theme_minimal()! Polygon provided. Using point on surface.Checking if spatial network structure is valid...Spatial network structure is valid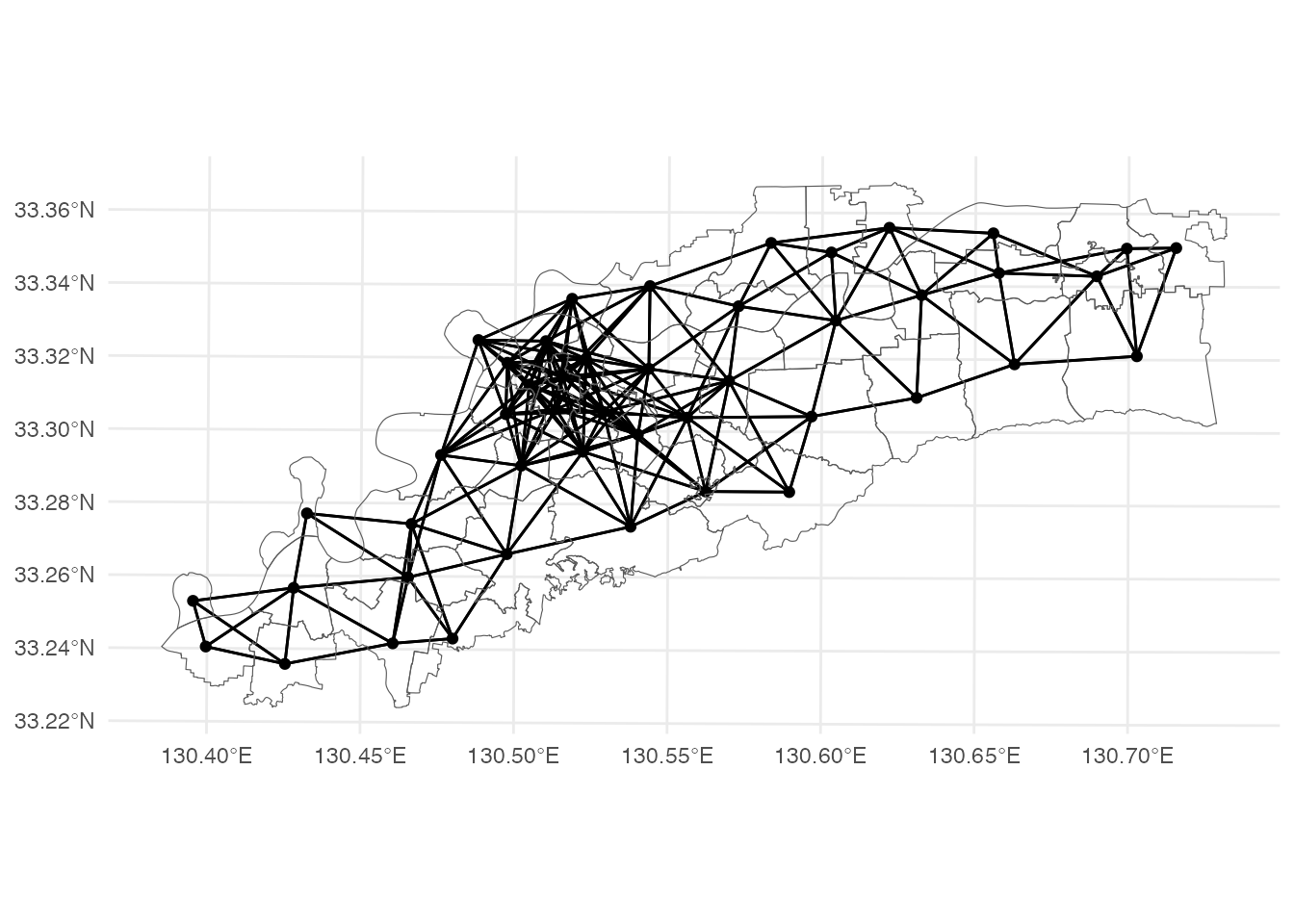
大域的空間統計量
大域的な空間的自己相関を評価する指標がいくつかありますが、今回はモランI統計量(Moran’s I Statistic)を紹介します。
モランI統計量
モランI統計量は、\(N\)個の地区で得られたデータ\(x_1, x_2,\ldots,x_N\)の空間的自己相関を、次の式で評価します。
\[ I = \frac{N}{\sum_i\sum_jw_{ij}}\frac{\sum_i\sum_jw_{ij}(x_j - \overline{x})(x_i - \overline{x})}{\sum_i(x_i - \overline{x})^2} \] ここで、\(\overline{x}\)はデータ\(x_i\)の平均値を意味しています。 また、\(w_{ij}\)は近接行列の\((i,j)\)要素、つまり地区\(i\)と地区\(j\)の近さを表すウェイトです。
\(w_{ij}\)が行基準化されている時には、\(\sum_jw_{ij}=1\)になりますから、\(\sum_i\sum_jw_{ij} = N\)です。 したがって上のモランI統計量の式は、
\[ I = \frac{\sum_i\sum_jw_{ij}(x_j - \overline{x})(x_i - \overline{x})}{\sum_i(x_i - \overline{x})^2} \] と書き直すことができます。
この統計量\(I\)は、自地区と他地区の相関の強さを評価する指標になっています。 また、この統計量はおよそ\(-1\)から\(1\)の間の数値をとります。 \(1\)に近い値のとき、互いに近い地区のデータが類似する(自地区の数値が高ければ近所も高い)ような、空間的自己相関かが強いことを意味します。 反対に\(-1\)に近い値のときは、自地区の数値が高ければ近所の数値が低くなるような関係にあることを意味します。
2つの変数の間の相関の程度を表す指標としてよく知られるピアソンの積率相関係数を思い出してみましょう。 その定義は次の式の通りです。 \[ r = \frac{\sum_i(x_i - \overline{x})(y_i - \overline{y})}{\sqrt{\sum_i(x_i - \overline{x})^2}\sqrt{\sum_i(y_i - \overline{y})^2}} \] モランI統計量を、このピアソンの積率相関係数の定義に合わせて書き換えてみます。 \[ I = \frac{\sum_i\sum_jw_{ij}(x_j - \overline{x})(x_i - \overline{x})}{\sqrt{\sum_i(x_i - \overline{x})^2}\sqrt{\sum_i(x_i - \overline{x})^2}} \] この2つの式を見比べると、モランI統計量が、自地区〔\((x_i-\overline{x})\)〕と近所〔\(\sum_iw_{ij}(x_i-\overline{x})\)〕との相関関係を計算しているのだということがわかるのではないでしょうか。
RによるモランI統計量の計算
モランI統計量を計算するデータとして、福岡県久留米市の校区別生産年齢人口を使いましょう。 また、近接行列としては、4近隣を採用することにしましょう。
モランI統計量は、sfdep::global_moranあるいはsfdep::global_moran_testで求めることができます。 sfdep::global_moran_testでは、空間相関の有無に関する検定ができます。
global_moran_test(x = kurume_knn$population,
nb = kurume_knn$nb,
wt = kurume_knn$wt)
Moran I test under randomisation
data: x
weights: listw
Moran I statistic standard deviate = 6.7741, p-value = 6.261e-12
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.608286179 -0.022222222 0.008663325 モランI統計量がおよそ0.6という結果になりました。 また、\(p\)値は十分に小さく、空間相関がないとは言えなさそうです。 ある程度の空間的自己相関があると言えそうです。
年少人口や高齢人口で計算すると、どのような結果になるかは、少し興味があるところです。 また、結果はデータだけでなく、どのような近隣行列を用いたかによっても変わります したがって、モランI統計量の結果を示すときには、データだけでなく、計算にどのような近隣行列を使ったのかを併せて示す必要があります。
局所的空間統計量
ローカル・モランI統計量
ピアソンの積率相関係数とモランI統計量を比べると、モランI統計量の分子にシグマ記号(\(\sum\))が1つ多いですよね。 そこで、モランI統計量の分子からシグマ記号を1つ外し、その分、大きさを揃えるために分母を\(1/N\)した指標\(I_i\)を考えます。
\[ I_i = \frac{(x_i - \overline{x})\sum_jw_{ij}(x_j - \overline{x})}{\frac{1}{N}\sum_j(x_j - \overline{x})^2} \]
この式で表される統計量は、ローカル・モランI統計量(Local Moran’s I Statistic)と呼ばれます。 \(I_i\)の値が正であれば、地区\(i\)のデータとその近所とデータが似ていることを、逆に負の値であれば近所と似ていないことを意味します。
通常、モランI統計量といえば、大域的空間統計量のことを指しますが、このローカル・モランI統計量と区別するために、グローバル・モランI統計量と呼ぶことがあります。
また、ローカル・モランI統計量とグローバル・モランI統計量には、 \[ I = \frac{1}{N}\sum_iI_i \] という関係があります。 ローカル・モランI統計量の平均がグローバル・モランI統計量に等しいという意味ですが、モランI統計量を地区ごとに分解したのがローカル・モランI統計量だということもできます。
Rによるローカル・モランI統計量の計算
sfdep::local_moran関数で、ローカル・モランI統計量を計算できます。 結果はいくつかの指標がdata.frame形式で返されます。
lmoran <- local_moran(x = kurume_knn$population,
nb = kurume_knn$nb,
wt = kurume_knn$wt)
glimpse(lmoran)Rows: 46
Columns: 12
$ ii <dbl> 2.24994627, 0.46915264, -0.04757528, -0.24075366, 3.35571…
$ eii <dbl> 0.0069344924, -0.0466334233, 0.0007729432, -0.0016417526,…
$ var_ii <dbl> 0.948362219, 0.397396363, 0.009048416, 0.044912825, 0.976…
$ z_ii <dbl> 2.30326778, 0.81819658, -0.50826974, -1.12827775, 3.55185…
$ p_ii <dbl> 0.0212637812, 0.4132449484, 0.6112641863, 0.2592026373, 0…
$ p_ii_sim <dbl> 0.040, 0.436, 0.608, 0.272, 0.004, 0.036, 0.024, 0.052, 0…
$ p_folded_sim <dbl> 0.020, 0.218, 0.304, 0.136, 0.002, 0.018, 0.012, 0.026, 0…
$ skewness <dbl> 0.3495992, -0.2793834, -0.2942937, 0.5304526, 0.2739056, …
$ kurtosis <dbl> 0.16450413, -0.27034310, -0.45648873, 0.10080792, -0.1187…
$ mean <fct> High-High, Low-Low, Low-High, High-Low, High-High, High-H…
$ median <fct> High-High, Low-Low, Low-High, High-Low, High-High, High-H…
$ pysal <fct> High-High, Low-Low, Low-High, High-Low, High-High, High-H…このうち、ローカル・モランI統計量はii列に格納されています。 また、空間相関の有無関する検定結果の\(p\)値がp_ii列に格納されています。 行(校区)の順番は、元データの行(校区)の順番と同じです。 このデータフレームを元データに連結します。 データの並び順が同じであることがわかっているので、dplyr::bind_cols関数で繋いでしまいます。
lmoran <- lmoran |>
select(local_moran = ii,
p_value = p_ii,
quadrant = mean)
kurume_res <-
kurume_knn |> bind_cols(lmoran)ggplotローカル・モランI統計量による塗り分け地図を作ってみましょう。
ggplot() +
geom_sf(data = kurume_res, aes(fill = local_moran)) +
scale_fill_distiller(palette = 'Spectral') +
theme_minimal()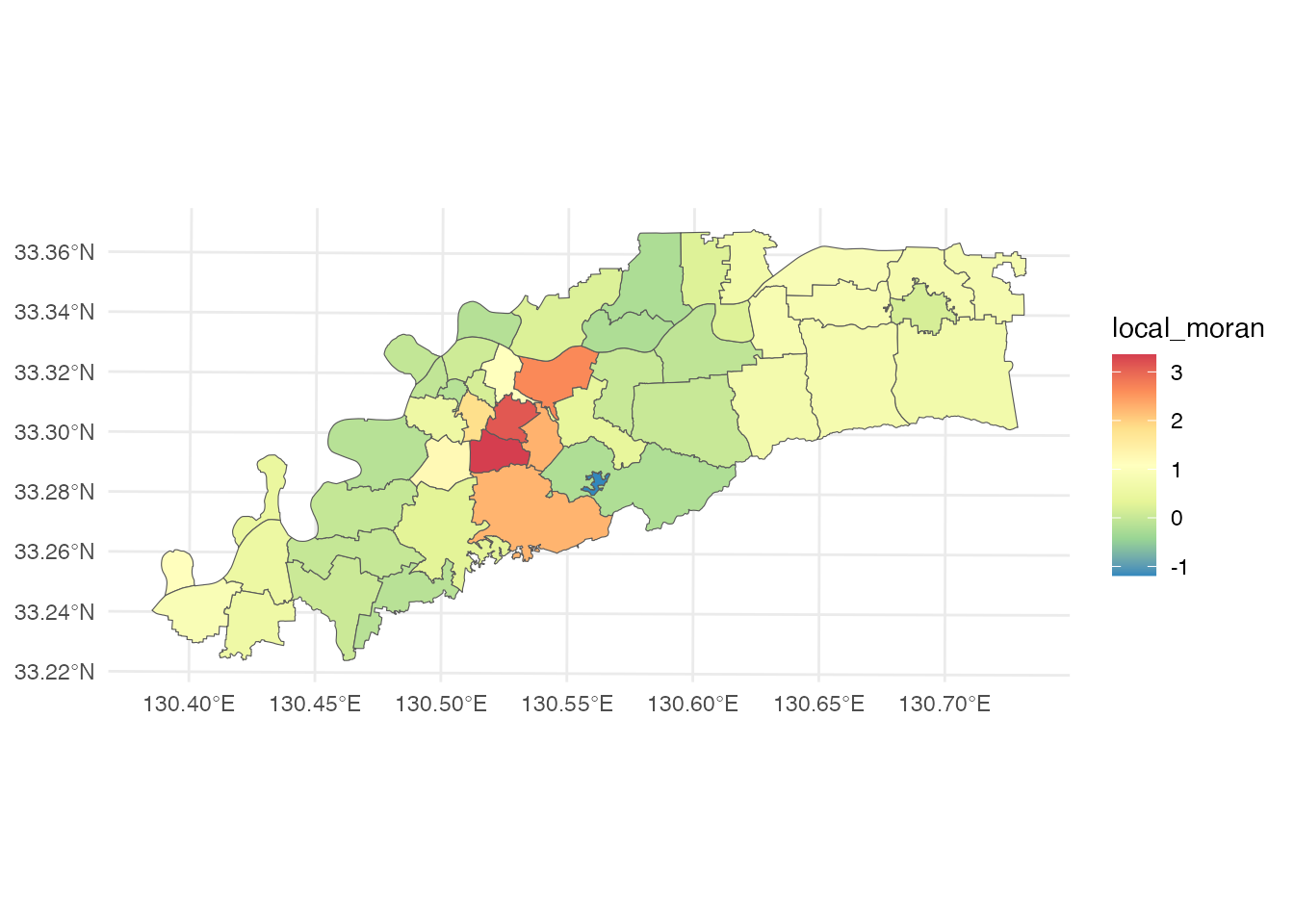
ローカル・モランI統計量が大きい校区は、西鉄久留米駅がある市中心部に多いことがわかります。 人口分布の図と見比べると、生産年齢人口の多い校区が集まっている市中心部で正の空間相関があるという結果は、納得できます。
モラン散布図
ローカル・モランI統計量の定義式をみると、この統計量は以下の場合に正の値をとることが分かります。
- \(x_i - \overline{x}>0\)かつ\(\sum_jw_{ij}(x_j - \overline{x})>0\)(自地区と近所が両方とも平均以上:High-High)
- \(x_i - \overline{x}<0\)かつ\(\sum_jw_{ij}(x_j - \overline{x})<0\)(自地区と近所が両方とも平均以下:Low-Low)
そして、\(I_i\)が負の値を取るのは、以下の場合です。
- \(x_i - \overline{x}>0\)かつ\(\sum_jw_{ij}(x_j - \overline{x})<0\)(自地区だけ平均以上:High-Low)
- \(x_i - \overline{x}<0\)かつ\(\sum_jw_{ij}(x_j - \overline{x})>0\)(自地区だけ平均以下:Low-High)
以上からわかるように、各地区は、\(x_i - \overline{x}\)と\(\sum_jw_{ij}(x_j - \overline{x})\)の値の符号によって、4つのクラスターに分類できます。
このとき、High-Highに分類された地区はホットスポット、Low-Lowに分類された地区はクールスポットと呼ばれます。
横軸に\(x_i - \overline{x}\)、縦軸に\(\sum_jw_{ij}(x_j - \overline{x})\)をとった平面に、各地区の値をプロットした図は、 モラン散布図(Moran scatterplot)と呼ばれます。 これは、横軸に地区の値を、縦軸に近隣の(重みつき)平均値(これを空間ラグと呼びます)をとった空間に、各地域のデータを載せた散布図です。 この平面において、第1象限がHigh-High(ポットスポット)、第2象限がLow-High、第3象限がLow-Low(クールスポット)、第4象限がHigh-Lowにそれぞれ対応します。
ggplotを使って、モラン散布図を描いてみましょう。 近隣の平均人口(空間ラグ)は、sfdep::st_lag関数で求めることができます。
kurume_res |>
mutate(lagged_population = st_lag(population, nb, wt),
significant = p_value <= 0.05) |>
ggplot(aes(x = population, y = lagged_population)) +
geom_point(aes(shape = significant, color = quadrant)) +
stat_summary(aes(xintercept = after_stat(x), y = 0), fun = mean,
geom = "vline", orientation = "y", linetype = 'dashed')+
stat_summary(aes(yintercept = after_stat(y), x = 0), fun = mean,
geom = "hline", orientation = "x", linetype = 'dashed') +
geom_smooth(method = "lm", se = FALSE) +
scale_color_discrete(direction = -1) +
scale_shape_manual(values = c(1, 19)) +
theme_minimal()`geom_smooth()` using formula = 'y ~ x'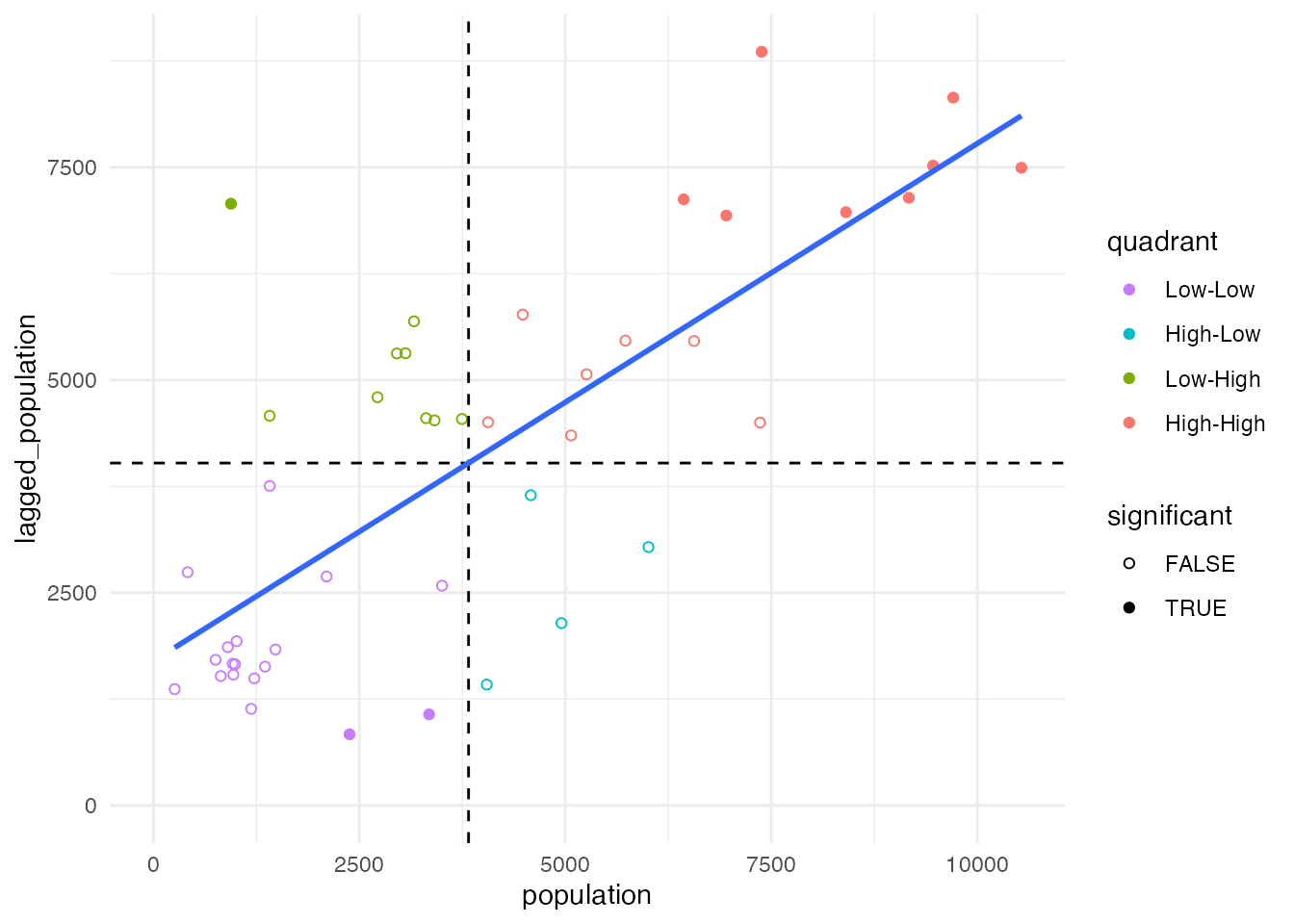
青い線は回帰直線です。 モラン散布図における回帰直線の傾きが、(グローバル)モランI統計量に相当します。
この結果を地図に表示してみましょう。 クラスター分類の塗り分け地図を書きますが、統計的に有意な地区のみに色をつけることにします。 このようにして作成された地図は、LISAクラスター地図(LISA cluster map)と呼ばれます(LISAはLocal Indicators of Spatial Association、すなわち局所的空間統計量のことです)。
ggplot() +
geom_sf(data = kurume) +
geom_sf(aes(fill = quadrant), data = filter(kurume_res, p_value <= 0.05)) +
scale_fill_discrete(direction = -1) +
theme_minimal()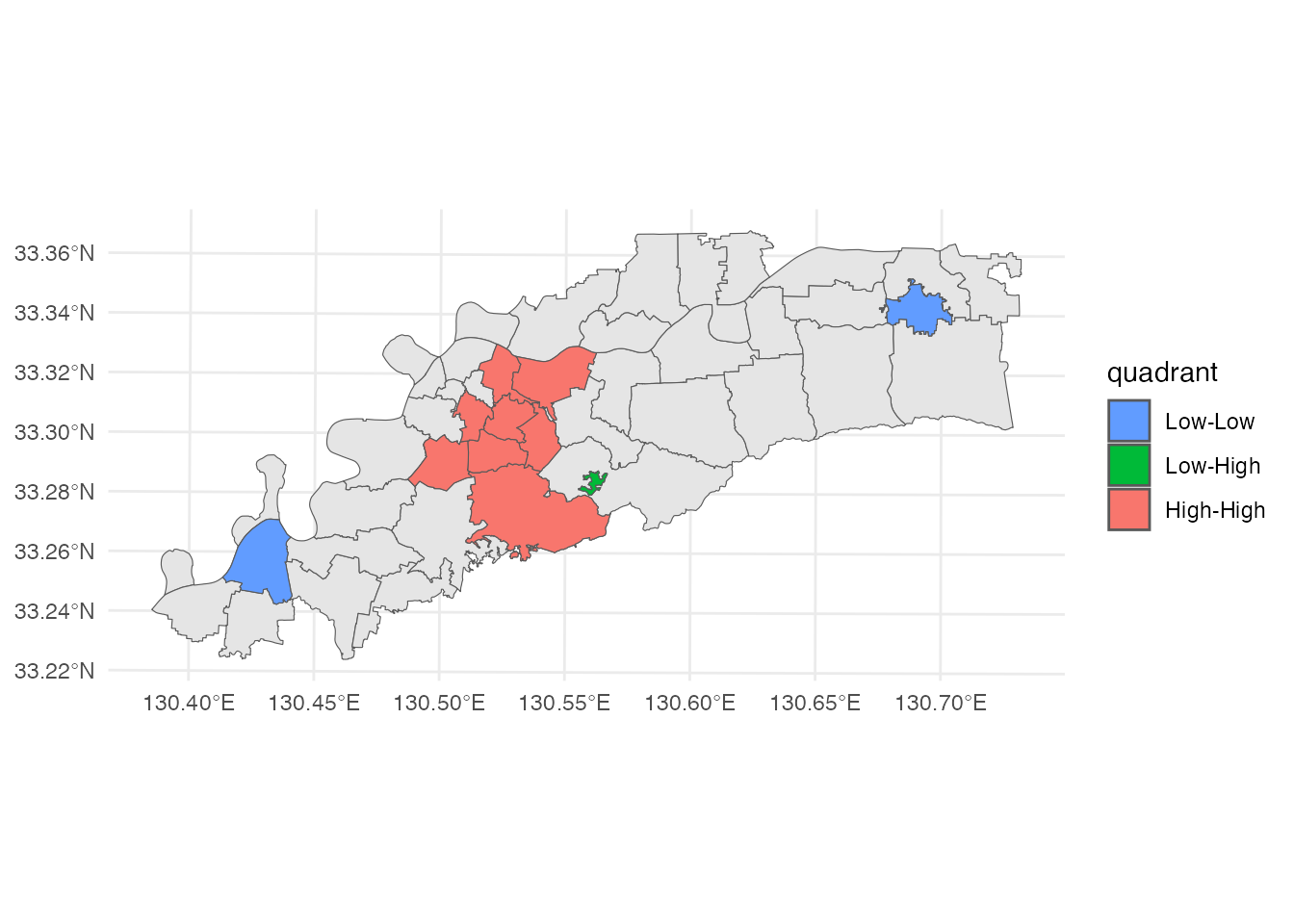
市中央部にホットスポットが、市西部にクールスポットが存在することが分かります。
このように、ローカル・モランI統計量は、空間データの分布について、地区ごとに評価・検定することができる便利なツールです。
